|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hille E. — Methods in classical and functional analysis |
|
|
 |
| Предметный указатель |
Matrix, symmetric 24
Matrix, transpose 24
Matrix, unit 21
Matrix, unitary 18
Maximum principle 256 272
Mean square convergence 158
Mean value(s) 437-474
Mean value(s), 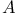 -average 437-451 -average 437-451
Mean value(s),  th power 95 140 447 th power 95 140 447
Mean value(s), arithmetic 95 152 428
Mean value(s), arithmetico-geometric 451
Mean value(s), functional equations of 439-449
Mean value(s), geometric 439 447
Mean value(s), H lder 450 lder 450
Mean value(s), harmonic 439 447
Mean value(s), property 255
Measurability, 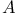 -, -,  - 113-115 236 468 - 113-115 236 468
Measurability, Lebesgue 119-123
Measurability, Lebesgue, of functions 119-123
Measurability, Lebesgue, of sets 112 119
Measurability, Lebesgue, radial 390
Measure, Carath odory 115 odory 115
Measure, inner 124 135
Measure, Lebesgue 112-119
Measure, outer 114
Measure, space 113
Measure, unit 114
Metzler, R. C. 420 423 425
Michal, A. D. 264
Mikusi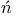 ski, J. 158 ski, J. 158
Miller antiderivations 372
Miller uniqueness theorem 433
Miller, J. B. 169 188 379
Minkowski  -norm 40 88 -norm 40 88
Minkowski convexity 380 395 411
Minkowski distance 40
Minkowski gauge function 40 317 319
Minkowski geometry of numbc/s 40
Minkowski inequality 90 139
Minkowski semi-norm 40
Minkowski support function 395
Minkowski, H. 40
Minors 7
Minors, principal 8
Mitrinovic, D. S. 379
Mittag — Leffler, G., partial fraction series 181
Modulus of continuity for ![$C[a, b]$](/math_tex/e77e794b3859783600b5f8f2bfed341e82.gif) 91 91
Modulus of continuity for ![$L_{p}[a, b]$](/math_tex/155ce4754a361ed7e5ed95c19d3f63cc82.gif) 145 149 145 149
Monotone Convergence Theorem 126 244
Morera theorem 258
Multiplication operator 426
Multiplication theorem 376 424
Multiplication, element-wise 19 64-65 80 86
Multiplication, scalar 2 8 19 52 56 63
Multiplicative inequalities 376-379
Na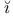 mark, M. A. 304 mark, M. A. 304
Nagumo postulates 285
Nagumo resolvent expansion 285 326
Nagumo uniqueness theorem 366 373
Nagumo, M. Nagumo inequality 366 373
Narici, L. 50 84
Neighborhood, epsilon 54
Neighborhood, Hausdorff 218
Neighborhood, strong, weak 224
Neumann series 177
Neumann, C. 177
Neumann, J., von 341 361
Newman, M. H. A. 84
Newton — Waring formula 473
Newton, Sir Isaac, potential 458
Ng uniqueness theorem 430-433
Ng, C. T. 436 437
Nilpotency 25
Norm 2 9 25 40 41 55 57 306
Norm, differentiability of 334
Norm, of  88 88
Norm, sup 87 97
Null space 57 306
Nullity 17
Operational calculus 296-304
Operational calculus, in Hilbert space 341-353
Operator, adjoint 44 77 322-325 333
Operator, antiderivation 372
Operator, bounded 57 165 305 310
Operator, Bourlet 424
Operator, Cayley 335 359
Operator, closed 307 310-316
Operator, commutator 296
Operator, conjugation 24
Operator, contraction 165-169
Operator, convolution 138 156
Operator, derivation 424
Operator, Dirichlet 360
Operator, hermitian 44 77 333 341-361
Operator, identity 65
Operator, inverse 14 58 65 165 322-325
Operator, involution 24 137 334
Operator, Jordan 296
Operator, multiplication 426
Operator, nilpotent 82 328
Operator, normal 78 334 338-341
Operator, order preserving 164 199
Operator, positive 199 345-348
Operator, projection 24 79 332 343 350-354
Operator, quasi-nilpotent 82 326
Operator, self-adjoint 77
Operator, shift 167
Operator, substitution 426
Operator, unitary 78
Order (ing), partial 165-165
Order (ing), preserving 164 199
Order (ing), total 162
Order (ing), under inclusion 162
Ordinate sets 123
Oscillation reducing 439
Ostrowski, A. 419 436
P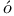 lya indicator 391 lya indicator 391
P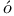 lya transfinite diameter 456 471 lya transfinite diameter 456 471
P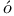 lya, G. 394 411 456 468 lya, G. 394 411 456 468
Parallelogram law 12 68 332
Parallelogram law, extended 12 69 453
Parseval, M. A., Parseval identity 72 151
Parts of Hermitian operator 78
Parts of real-valued function 121
Peano postulates 85
Peano, G. 85
Pecking order 329
Perlis, S., circle product 279
Perp 74
Perspectivity 430
Pettis, B. J. 248
Phillips, R. S. 248 275 304 330 385 410
Phragm n growth indicator 191 411 n growth indicator 191 411
Phragm n, E. 263 n, E. 263
Picard successive approximations 194-199
Picard transform 169 172
Picard two-point theorem 433 436
Picard, E. 169 194
Pl cker, J. 396 cker, J. 396
Poincar , H. 184 , H. 184
Point 1 9 51
Point coordinates 395
Point spectrum 183 328
Poisson, S. D., transform 172
Polar form 43 77 333
Polar plane 43
Polar solids 396
Pole of  -holomorphic function 255 -holomorphic function 255
Pole of meromorphic function 183
Pole of polar convex solids 396
| Pole of polar plane 43
Polynomial, 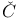 eby eby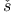 ev 459 464 ev 459 464
Polynomial, abstract 264 274
Polynomial, Bernstein 101
Polynomial, Fekete 471
Polynomial, positive 344
Porter, M. B. 258
Positivity 198-199 343-348
Postulates, A-averages 437-439
Postulates, addition 52
Postulates, distance 40 54
Postulates, equality 52
Postulates, multiplication 80
Postulates, norm 39 55
Postulates, Peano 85
Postulates, scalar multiplication 52
Potential, 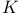 470 470
Potential, logarithmic 456 465 472
Potential, M. Riesz 474
Potential, Newtonian 457 465 469
Potential, theories 467-474
Power set 113
Power, abstract 264
Power, means 140
Principle of absolute integrability 240
Principle of maximum 256-257 272
Principle of repeated averages 438
Principle of uniform boundedness 212-217
Product, box 395
Product, cartesian 56
Product, circle 279
Product, cross 8
Product, dot 4
Product, inner 4 9 67
Product, scalar 8 52
Product, space 56
Product, vector 8
Projection 24 66 79 326 332
Property, absolute integrability 129
Property, mean value 255
Pythagoras 68
Pythagoras theorem 69 332
Quadratic form 42 77 333
Quadric surface 42
Quasi-inverse 279
Quasi-nilpotent 82
Quotient algebra 292
Radfmacher, H. 411
Radius, spectral 83 278
Radon, J. 469
RANGE 14 58 305
Range, numerical 335-341
Rank 17
Residual spectrum 328 337
Residue class 292
Resolution of the identity 34 50 333 343
Resolution, spectral 326
Resolvent 28-36 65-66 83-84 281-290
Resolvent, spectral representation of 32 50 342 359
Resolvent-equations 36 281-290 413
Resolvent-kernel 180-184
Reverse, revertible 279
Riccati, J. F. Count, Riccati equations 289 290
Rickart, C. E. 304
Riemann — Stieltjes integral 103
Riemann — Stieltjes integral, abstract 230-236
Riesz functionals on ![$C[a, b]$](/math_tex/e77e794b3859783600b5f8f2bfed341e82.gif) 104 104
Riesz on 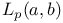 146 146
Riesz positive operation theorem 345 346
Riesz potential 474
Riesz splitting theorem 349-350
Riesz — Fischer theorem 156
Riesz, F. 55 249 322 342
Riesz, M. 464
Rijnierse, P. J. 416 436
Robin constant 469
Robin, G. 469
Rosenbaum, R., subadditive functions 385 411
Rota, G. — C., Rota — Landau — Kallman theorem 167 168
Runge, C. 258
Scalar multiplication of linear transformations 19 63
Scalar multiplication of matrices 19
Scalar multiplication of sequences 86
Scalar multiplication of vectors 2 8 52
Schaeffer, H. H. 187 330
Schmidt characteristic values 183
Schmidt — Gram-orthogonalization process 3-7 12 69
Schmidt, E. 4
Schr der, E., functional equation 426 436 464 der, E., functional equation 426 436 464
Schwartz, J. 248 304 330 361
Schwarz lemma 257
Schwarz — Bounyakovsky-inequality 139
Schwarz, H. A. 139
Sebastiao e Silva, J. 264
Semi-group, infinitesimal generator of 167
Semi-group, neutral element of 165
Semi-group, of operators 165 167 423
Semi-group, Poisson 172
Semi-module 386-400
Semi-module, angular 386
SEQUENCE 54
Sequence, Cauchy 5
Sequence, diagonal 22
Sequence, spaces 85-96
Sequence, subadditive 278 385
Series, Fourier, abstract 70-73
Series, Fourier, trigonometric 149-158
Series, gap = lacunary 157
Series, Taylor 255
Set, A-measurable 113
Set, closed, open 54
Set, compact 160
Set, conditionally, sequentially 161
Set, convex 13
Set, dense, nowhere dense 54
Set, difference 218 296
Set, dissolvent 279
Set, infimum 163
Set, lim, inf, sup 119
Set, measurable 113
Set, ordinate 123
Set, power 113
Set, product 296
Set, resolvent 65 83 96 109 277 325
Set, spectral 326
Set, sub 13
Set, sum 387
Set, supremum 163
Set, void 112
Set-function 114 253 456 459 468
simplex 452
Simplicial problem 452
Singular points 375
Singular points, rate of growth at 374 415-417
Singular points, regular, irregular 376
Sinusoid 395
Sobczyk, A., — Bohnenblust theorem 319
Space, 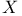 equals equals 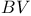 103 107 111 103 107 111
Space, 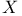 equals equals ![$C[a, b]$](/math_tex/e77e794b3859783600b5f8f2bfed341e82.gif) 96 101 96 101
Space, 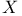 equals equals ![$C^{k}[a, b]$](/math_tex/cd58d9158fbf4f4d721a3c4b7264057682.gif) 105 105
Space, 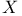 equals equals 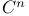 8-13 8-13
Space, 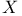 equals equals  105 105
Space, 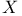 equals equals  9 9
Space, 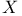 equals equals  18-28 18-28
Space, 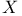 equals equals ![$\mathfrak{M}^{n}C[a, b]$](/math_tex/290994bf125ce90e3d3afa541011089682.gif) 104 104
Space, 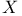 equals Lebesgue 112-156 136-149 equals Lebesgue 112-156 136-149
Space, 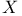 equals sequence 85-96 equals sequence 85-96
Space, abstract 51
Space, adjoint = dual 60 218
Space, Banach 51-56
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



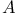 -average
-average  th power
th power  lder
lder -
- odory
odory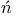 ski, J.
ski, J. -norm
-norm ![$C[a, b]$](/math_tex/e77e794b3859783600b5f8f2bfed341e82.gif)
![$L_{p}[a, b]$](/math_tex/155ce4754a361ed7e5ed95c19d3f63cc82.gif)
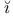 mark, M. A.
mark, M. A. 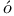 lya indicator
lya indicator  cker, J.
cker, J.  -holomorphic function
-holomorphic function 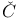 eby
eby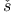 ev
ev 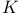
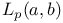
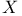 equals
equals 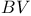
![$C^{k}[a, b]$](/math_tex/cd58d9158fbf4f4d721a3c4b7264057682.gif)
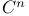



![$\mathfrak{M}^{n}C[a, b]$](/math_tex/290994bf125ce90e3d3afa541011089682.gif)