|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Riley, Hobson Ч Mathematical Methods for Physics and Engineering |
|
|
 |
| ѕредметный указатель |
Spur of a matrix 263Ч264
Spur, of a matrix see "Trace of
Square matrices 254
Square, symmetries of 942
Square-wave, Fourier series for 424 425
Stagnation points of fluid flow 727
Standard deviation  988 988
Standard deviation  of sample 1067 of sample 1067
standing waves 626
Stationary values of functions of one real variable 51Ч53
Stationary values of functions of several real variables 165Ч170
Stationary values of integrals 835
Stationary values under constraints see "Lagrange undetermined multipliers"
Statistical tests, and hypothesis testing 1120
Statistics 961 1064Ч1140
Statistics, describing data 1065Ч1072
Statistics, estimating parameters 1072Ч1097 1140
Stirling's approximation 1027 1203
Stirling's asymptotic series 1203
Stokes' equation 858
Stokes' theorem 394 412Ч415
Stokes' theorem for tensors 804
Stokes' theorem, physical applications 414
Stokes' theorem, related theorems 413
Strain tensor 802
Stratified sampling, in Monte Carlo methods 1172
Streamlines and complex potentials 727
Stress tensor 802
Stress waves 829
String, loaded 857
String, plucked 705
String, transverse vibrations of 609 848
Student's t-distribution, comparison of means 1131
Student's t-distribution, critical points table 1130
Student's t-distribution, normalisation 1128
Student's t-distribution, one/two-tailed confidence limits 1130
Student's t-distribution, plots 1129
Student's t-test 1126Ч1132
Sturm Ч Liouville equations 591Ч597
Sturm Ч Liouville equations, boundary conditions 592
Sturm Ч Liouville equations, examples 593Ч597
Sturm Ч Liouville equations, examples, associated Legendre equation 594Ч595
Sturm Ч Liouville equations, examples, Bessel equation 595
Sturm Ч Liouville equations, examples, Chebyshev equation 597
Sturm Ч Liouville equations, examples, Hermite equation 596
Sturm Ч Liouville equations, examples, hypergeometric equation 603
Sturm Ч Liouville equations, examples, Laguerre equation 596Ч597
Sturm Ч Liouville equations, examples, Legendre equation 593Ч594
Sturm Ч Liouville equations, examples, simple harmonic oscillator 595
Sturm Ч Liouville equations, manipulation to self-adjoint form 592Ч593
Sturm Ч Liouville equations, two independent variables 860
Sturm Ч Liouville equations, variational approach 849Ч854
Sturm Ч Liouville equations, weight function 849
Sturm Ч Liouville equations, zeroes of eigenfunctions 603
Subgroups 903Ч905
Subgroups, index 908
Subgroups, normal 905
Subgroups, order 903
Subgroups, order, Lagrange's theorem 907
Subgroups, proper 903
Subgroups, trivial 903
Submatrices 272Ч273
Subscripts and superscripts 111
Subscripts and superscripts, contra- and covariant 805
Subscripts and superscripts, covariant derivative 818
Subscripts and superscripts, dummy 111
Subscripts and superscripts, free 111
Subscripts and superscripts, partial derivative 818
Subscripts and superscripts, summation convention 111 804
Substitution, integration by 66Ч68
Summation convention 111 804
Summation of series 119Ч127
Summation of series, arithmetic 120
Summation of series, arithmetico-geometric 121
Summation of series, contour integration method 764Ч765
Summation of series, difference method 122Ч123
Summation of series, Fourier series method 433
Summation of series, geometric 120
Summation of series, powers of natural numbers 124Ч125
Summation of series, transformation methods 125Ч127
Summation of series, transformation methods, differentiation 125
Summation of series, transformation methods, integration 125
Summation of series, transformation methods, substitution 126
Superposition methods for ODE 581 597Ч601
Superposition methods for PDE 650Ч657
Surface integrals and divergence theorem 407
Surface integrals of scalars, vectors 395Ч402
Surface integrals, Archimedean up thrust 402 416
Surface integrals, physical examples 401
Surfaces 351Ч353
Surfaces of revolution 75Ч76
Surfaces, area of 352
Surfaces, area of, cone 75Ч76
Surfaces, area of, solid, and Pappus' theorem 198Ч200
Surfaces, area of, sphere 352
Surfaces, coordinate curves 352
Surfaces, normal to 352 356
Surfaces, parametric equations 351
Surfaces, quadratic 297
Surfaces, tangent plane 352
Symmetric functions 422
Symmetric functions and Fourier series 425 426
Symmetric functions and Fourier transforms 451
Symmetric matrices 275
Symmetric matrices, general properties see "Hermitian matrices"
Symmetric tensors 787
Symmetry operations on molecules 883
Symmetry operations, order of application 886
Symmetry, and equivalence relations 906
t substitution 66Ч67
t-test see "Student's t-test"
Tangent planes to surfaces 352
Tangent vectors to space curves 348
tanh, hyperbolic tangent see "Hyperbolic functions"
Taylor series 139Ч144
Taylor series and finite differences 1179 1186
Taylor series and Taylor's theorem 139Ч142 747
Taylor series as solution of ODE 1183Ч1184
Taylor series for functions of a complex variable 747Ч748
Taylor series for functions of several real variables 163Ч165
Taylor series, approximation errors 142Ч143
Taylor series, approximation errors, in numerical methods 1156 1166
Taylor series, remainder term 141
Taylor series, required properties 139
Taylor series, standard forms 139
Tensors see "Cartesian tensors" "Cartesian particular
Test statistic 1120
Tetrahedral group 957
Tetrahedron, mass of 197
Tetrahedron, volume of 195
Thermodynamics, first law of 179
Thermodynamics, Maxwell's relations 179Ч181
Top-hat function see "Rectangular distribution"
Torque, vector representation of 227
Torsion of space curves 348
Total derivative 157
Total differential 157
Trace of a matrix 263Ч264
Trace of a matrix and second-order tensors 788
Trace of a matrix as sum of eigenvalues 285 292
Trace of a matrix, invariance under similarity transformations 289 934
Trace of a matrix, trace formula 292
Transcendental equations 1150
Transformation matrix 288 294
Transformations, active and passive 797
Transformations, conformal 730Ч738
Transforms, integral see "Integral transforms" "Fourier "Laplace
Transients in diffusion equation 656
Transients in electric circuits 491
Transitivity, and equivalence relations 906
| Transpose of a matrix 255 260Ч261
Transpose of a matrix, product rule 261
Transverse vibrations, membrane 610 673 702
Transverse vibrations, rod 704
Transverse vibrations, string 609
Trapezium rule 1166Ч1167
Trial functions for eigenvalue estimation 852
Trial functions for particular integrals of ODE 500
Trials 961
Triangle inequality 251 586
Triangle, centroid of 220Ч221
Triangular matrices 274
Tridiagonal matrices 1162Ч1164 1190 1193
Trignometric identities 15
Trigonometric identities 10
Triple integrals see "Multiple integrals"
Uncertainty principle (Heisenberg) 441Ч443
Undetermined coefficients, method of 500
Undetermined multipliers see "Lagrange undetermined multipliers"
Uniform distribution 1036
Union 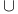 , probability for see "Probability for union" , probability for see "Probability for union"
Uniqueness theorem, Laplace equation 676
Uniqueness theorem, Poisson equation 638Ч640
Unit step function see "Heaviside function"
Unit vectors 223
Unitary, matrices 276
Unitary, matrices, eigenvalues and eigenvectors 283
Unitary, representations 928
Unitary, transformations 290
Upper triangular matrices 274
Variable end-points see "End-points for variations variable"
Variable, dummy 62
Variance  , from MGF 1005 , from MGF 1005
Variance  988 988
Variance  from PGF 1001 from PGF 1001
Variance  of dependent RV 1044 of dependent RV 1044
Variance  of sample 1067 of sample 1067
Variation of parameters 514Ч516
Variation, constrained 844Ч846
Variational principles, physical 846Ч849
Variational principles, physical, Fermat 846
Variational principles, physical, Hamilton 847
Variations, calculus of see "Calculus of variations"
Vector operators 353Ч375
Vector operators, acting on sums and products 360Ч361
Vector operators, combinations of 361Ч363
Vector operators, curl 359 374
Vector operators, del  354 354
Vector operators, del squared 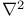 358 358
Vector operators, divergence (div) 358
Vector operators, geometrical definitions 404 406
Vector operators, gradient operator (grad) 354Ч358 373
Vector operators, identities 362 827
Vector operators, Laplacian 358 374
Vector operators, non-Cartesian 363Ч375
Vector operators, tensor forms 820Ч824
Vector operators, tensor forms, curl 823
Vector operators, tensor forms, divergence 821Ч822
Vector operators, tensor forms, gradient 821
Vector operators, tensor forms, Laplacian 822
Vector product 226Ч228
Vector product in Cartesian coordinates 228
Vector product, anticommutativity 226
Vector product, definition 226
Vector product, determinant form 228
Vector product, non-associativity 226
Vector spaces 247Ч252 955
Vector spaces of infinite dimensionality 583Ч586
Vector spaces of infinite dimensionality, associativity of addition 583
Vector spaces of infinite dimensionality, basis functions 583Ч584
Vector spaces of infinite dimensionality, commutativity of addition 583
Vector spaces of infinite dimensionality, defining properties 583
Vector spaces of infinite dimensionality, Hilbert spaces 584Ч586
Vector spaces of infinite dimensionality, inequalities: Bessel, Schwarz, triangle 586
Vector spaces, action of group on 930
Vector spaces, associativity of addition 247
Vector spaces, basis vectors 248Ч249
Vector spaces, commutativity of addition 247
Vector spaces, complex 247
Vector spaces, defining properties 247
Vector spaces, dimensionality 248
Vector spaces, inequalities: Bessel, Schwarz, triangle 251Ч252
Vector spaces, invariant 930 955
Vector spaces, matrices as an example 257
Vector spaces, parallelogram equality 252
Vector spaces, real 247
Vector spaces, span of a set of vectors in 247
Vector triple product 230
Vector triple product, identities 230
Vector triple product, non-associativity 230
Vectors as first-order tensors 781
Vectors as geometrical objects 246
Vectors, algebra of 216Ч238
Vectors, algebra of, addition and subtraction 217Ч218
Vectors, algebra of, addition and subtraction, in component form 222
Vectors, algebra of, angle between 225
Vectors, algebra of, associativity of addition and subtraction 217
Vectors, algebra of, commutativity of addition and subtraction 217
Vectors, algebra of, multiplication by a complex scalar 226
Vectors, algebra of, multiplication by a scalar 218
Vectors, algebra of, multiplication of see "Scalar product" "Vector
Vectors, algebra of, outer product 785
Vectors, applications, centroid of a triangle 220Ч221
Vectors, applications, equation of a line 230Ч231
Vectors, applications, equation of a plane 231Ч232
Vectors, applications, equation of a sphere 232
Vectors, applications, finding distance from a line to a line 235Ч236
Vectors, applications, finding distance from a line to a plane 236Ч237
Vectors, applications, finding distance from a point to a line 233Ч234
Vectors, applications, finding distance from a point to a plane 234Ч235
Vectors, applications, intersection of two planes 232
Vectors, base 342
Vectors, calculus of 340Ч375
Vectors, calculus of, differentiation 340Ч345 350
Vectors, calculus of, integration 345Ч346
Vectors, calculus of, line integrals 383Ч395
Vectors, calculus of, surface integrals 395Ч402
Vectors, calculus of, volume integrals 402 403
Vectors, column 255
Vectors, compared with scalars 216Ч217
Vectors, component form 221Ч222
Vectors, derived quantities, curl 359
Vectors, derived quantities, derivative 340
Vectors, derived quantities, differential 344 350
Vectors, derived quantities, divergence (div) 358
Vectors, derived quantities, reciprocal 237Ч238 372 804 808
Vectors, derived quantities, vector fields 353
Vectors, derived quantities, vector fields, curl 412
Vectors, derived quantities, vector fields, divergence 358
Vectors, derived quantities, vector fields, flux 401
Vectors, derived quantities, vector fields, rate of change 356
Vectors, examples of 216
Vectors, graphical representation of 216Ч217
Vectors, irrotational 359
Vectors, magnitude of 222Ч223
Vectors, non-Cartesian 342 364 368
Vectors, notation 216
Vectors, physical, acceleration 341
Vectors, physical, angular momentum 241
Vectors, physical, angular velocity 227 241 359
Vectors, physical, area 399Ч401 414
Vectors, physical, area of parallelogram 227 228
Vectors, physical, force 216 217 224
Vectors, physical, moment/torque of a force 227
Vectors, physical, velocity 341
Vectors, polar and axial 798
Vectors, solenoidal 358 395
Vectors, span of 247
Velocity vectors 341
Venn diagrams 961Ч966
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте




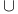 , probability for
, probability for  , from MGF
, from MGF