|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Riley, Hobson — Mathematical Methods for Physics and Engineering |
|
|
 |
| Предметный указатель |
Legendre equation, general series solution 556
Legendre functions 556
Legendre functions 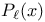 , associated Legendre functions 703 , associated Legendre functions 703
Legendre functions of second kind 557
Legendre linear equation 509
Legendre polynomials 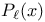 557 557
Legendre polynomials 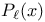 in Gaussian integration 1168 in Gaussian integration 1168
Legendre polynomials 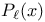 , associated Legendre functions 666 , associated Legendre functions 666
Legendre polynomials 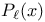 , generating function 562—564 594 , generating function 562—564 594
Legendre polynomials 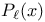 , graph of 557 , graph of 557
Legendre polynomials 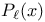 , normalisation 557 559 , normalisation 557 559
Legendre polynomials 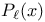 , orthogonality 560 594 668 , orthogonality 560 594 668
Legendre polynomials 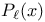 , recurrence relation 562 , recurrence relation 562
Legendre polynomials 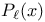 , Rodrigues' formula 559 594 , Rodrigues' formula 559 594
Leibnitz' rule for differentiation of integrals 181
Leibniz' theorem 49—51
Length of a vector 222—223
Length of plane curves 74—75 347
Length of space curves 347
Length of tensor form 831
Levi-Civita symbol see " Levi-Civita tensor" Levi-Civita tensor"
Likelihood function 1097
Limits 144—147
Limits of functions containing exponents 145
Limits of integrals 60
Limits of integrals, containing variables 191
Limits of products 144
Limits of quotients 144—147
Limits of sums 144
Limits, definition 144
Limits, L'Hopital's rule 145—147
Line charge, electrostatic potential 726 738
Line integrals and Cauchy integrals 745—747
Line integrals and Stokes' theorem 412—415
Line integrals of scalars 383—393
Line integrals of vectors 383—395
Line integrals, physical examples 387
Line integrals, round closed loop 392
Line, vector equation of 230—231
Linear dependence and independence of basis vectors 221
Linear dependence and independence, definition in a vector space 247
Linear dependence and independence, relationship with rank 272
Linear differential operator  517 551 581 517 551 581
Linear differential operator  for Sturm — Liouville equation 591—593 for Sturm — Liouville equation 591—593
Linear differential operator  , adjoint , adjoint  587 587
Linear differential operator  , eigenfunctions see "Eigenfunctions" , eigenfunctions see "Eigenfunctions"
Linear differential operator  , eigenvalues see "Eigenvalues of , eigenvalues see "Eigenvalues of
Linear differential operator  , Hermitian (self-adjoint) 583 587—591 , Hermitian (self-adjoint) 583 587—591
Linear equations, differential, first-order ODE 480
Linear equations, differential, general ODE 496—523
Linear equations, differential, ODE with constant coefficients 498—509
Linear equations, differential, ODE with variable coefficients 509—523
Linear independence of functions 497
Linear independence of functions, Wronskian test 497 538
Linear integral operator  864 864
Linear integral operator  and Schmidt — Hilbert theory 875—877 and Schmidt — Hilbert theory 875—877
Linear integral operator  , Hermitian conjugate 864 , Hermitian conjugate 864
Linear integral operator  , inverse 865 , inverse 865
Linear interpolation for algebraic equations 1152—1153
Linear least squares, method of 1114
Linear molecules, normal modes of 326—328
Linear molecules, symmetries of 919
Linear operators 252—254
Linear operators in a particular basis 253
Linear operators, associativity 254
Linear operators, distributivity over addition 254
Linear operators, eigenvalues and eigenvectors 277
Linear operators, inverse 254
Linear operators, non-commutativity 254
Linear operators, particular: identity, null/zero, singular/non-singular 254
Linear operators, properties 254
Linear vector spaces see "Vector spaces"
Liouville's theorem 747
Ln of a complex number 102—103 720
ln, Maclaurin series for 143
Log-likelihood function 1100
Longitudinal vibrations in a rod 610
Lottery (UK), and hypergeometric distribution 1016
Lower triangular matrices 274
Maclaurin series 141
Maclaurin series, standard expressions 143
Madelung constant 151
Magnetic dipole 224
Magnitude of a vector 222—223
Magnitude of a vector in terms of scalar/dot product 225
Marginal distributions 1040
Mass of non-uniform bodies 196
Matrices 246—312
Matrices as a vector space 257
Matrices as arrays of numbers 254
Matrices as representation of a linear operator 254
Matrices, algebra of 255
Matrices, algebra of, addition 256—257
Matrices, algebra of, and normal modes see "Normal modes"
Matrices, algebra of, change of basis 288—290
Matrices, algebra of, Cholesky separation 318
Matrices, algebra of, diagonalisation see "Diagonalisation of matrices"
Matrices, algebra of, multiplication 257—259
Matrices, algebra of, multiplication by a scalar 256—257
Matrices, algebra of, multiplication, and common eigenvalues 283
Matrices, algebra of, multiplication, commutator 314
Matrices, algebra of, multiplication, non-commutativity 259
Matrices, algebra of, numerical methods see "Numerical methods for simultaneous linear equations"
Matrices, algebra of, similarity transformations see "Similarity transformations"
Matrices, algebra of, simultaneous linear equations see "Simultaneous linear equations"
Matrices, algebra of, subtraction 256
Matrices, column 255
Matrices, derived, adjoint 261—263
Matrices, derived, complex conjugate 261—263
Matrices, derived, Hermitian conjugate 261—263
Matrices, derived, inverse see "Inverse matrices"
Matrices, derived, transpose 255
Matrices, elements 254
Matrices, elements, minors and cofactors 264
Matrices, identity/unit 259
Matrices, properties of, anti-Hermitian see "Anti-Hermitian matrices"
Matrices, properties of, antisymmetric/skew-symmetric 275
Matrices, properties of, determinant see "Determinants"
Matrices, properties of, diagonal 273
Matrices, properties of, eigenvalues see "Eigenvalues"
Matrices, properties of, eigenvectors see "Eigenvectors"
Matrices, properties of, Hermitian see "Hermitian matrices"
Matrices, properties of, normal see "Normal matrices"
Matrices, properties of, nullity 298
Matrices, properties of, order 254
Matrices, properties of, orthogonal 275—276
Matrices, properties of, rank 272
Matrices, properties of, square 254
Matrices, properties of, symmetric 275
Matrices, properties of, trace/spur 263
Matrices, properties of, triangular 274
Matrices, properties of, tridiagonal 1162—1164 1190
Matrices, properties of, unitary see "Unitary matrices"
Matrices, row 255
Matrices, zero/null 259
Matrix elements in quantum mechanics as integrals 945
Matrix elements in quantum mechanics, dipole 950—951 957
Maxima and minima (local) of a function of constrained variables see "Lagrange undetermined multipliers"
Maxima and minima (local) of a function of one real variable 51—53
Maxima and minima (local) of a function of one real variable, sufficient conditions 52
Maxima and minima (local) of a function of several real variables 165—170
Maxima and minima (local) of a function of several real variables, sufficient conditions 167 170
Maximum modulus theorem 756
Maximum-likelihood, method of 1097—1113
Maximum-likelihood, method of extended 1112
Maximum-likelihood, method of, bias 1102
Maximum-likelihood, method of, data modelling 1097
Maximum-likelihood, method of, estimator 1098
Maximum-likelihood, method of, log-likelihood function 1100
Maximum-likelihood, method of, parameter estimation 1097
| Maximum-likelihood, method of, transformation invariance 1102
Maxwell — Boltzmann statistics 980
Maxwell's electromagnetic equations 379 414 828
Maxwell's thermodynamic relations 179—181
Mean  from MGF 1005 from MGF 1005
Mean  from PGF 1000 from PGF 1000
Mean  of RYD 986—987 of RYD 986—987
Mean  of sample 1066 of sample 1066
Mean  of sample: geometric, harmonic, root mean square 1066 of sample: geometric, harmonic, root mean square 1066
Mean value of a function of one variable 73—74
Mean value of a function of several variables 202
Mean value theorem 57—58
Median of RVD 987
Membrane, deformed rim 658—660
Membrane, normal modes 673 954
Membrane, transverse vibrations 610 673 702 954
Method of images 639 693—699 738
Method of images, disc (section of cylinder) 699 701
Method of images, infinite plate 694
Method of images, intersecting plates in two dimensions 696
Method of images, sphere 697—698 706
Metric tensor 806—809 812
Metric tensor and Christoffel symbols 815
Metric tensor and scale factors 806 821
Metric tensor, covariant derivative of 831
Metric tensor, determinant 806 813
Metric tensor, determinant, derivative of 822
Metric tensor, length element 806
Metric tensor, raising/lowering index 808 812
Metric tensor, scalar product 807
Metric tensor, volume element 806 830
mgf see "Moment generating functions"
Milne's method 1182
Minimum-variance estimator 1075
Minor of a matrix element 264
Mixed, components of tensor 806 811 818
ML estimator 1098
ML estimators 1098
ML estimators, bias 1102
ML estimators, confidence limits 1104
ML estimators, efficiency 1103
ML estimators, transformation invariance 1102
Mod N, multiplication 891
Mode of RVD 987
MODULO see "mod N multiplication"
Modulus of a complex number 90
Modulus of a vector see "Magnitude of a vector molecules"
Molecules, bonding in 945 947—950
Molecules, dipole moments of 919—920
Molecules, symmetries of 919
Moment generating functions (MGF) 1004—1009
Moment generating functions (MGF) and central limit theorem 1037—1038
Moment generating functions (MGF) and PGF 1005
Moment generating functions (MGF), mean and variance 1005
Moment generating functions (MGF), particular distributions, binomial 1012
Moment generating functions (MGF), particular distributions, exponential 1033
Moment generating functions (MGF), particular distributions, Gaussian 1005 1027
Moment generating functions (MGF), particular distributions, Poisson 1019
Moment generating functions (MGF), properties 1005
Moments of inertia and inertia tensor 800
Moments of inertia of disc 211
Moments of inertia of rectangular lamina 201
Moments of inertia of right circular cylinder 212
Moments of inertia of sphere 208
Moments of inertia, definition 201
Moments of inertia, perpendicular axes theorem 212
Moments of RVD 989
Moments, central 990
Moments, vector representation of 227
Momentum as first-order tensor 782
Monomorphism 903
Monte Carlo methods, antithetic variates 1174
Monte Carlo methods, control variates 1173
Monte Carlo methods, crude 1172
Monte Carlo methods, hit or miss 1174
Monte Carlo methods, importance sampling 1172
Monte Carlo methods, multiple integrals 1176
Monte Carlo methods, of integration 1170—1177
Monte Carlo methods, random number generation 1177
Monte Carlo methods, stratified sampling 1172
Morera's theorem 744
Multinomial distribution 1050—1051
Multinomial distribution and multiple Poisson distribution 1060
Multiple angles, trigonometric formulae 10
Multiple integrals, application in finding, area and volume 194—196
Multiple integrals, application in finding, mass, centre of mass and centroid 196—198
Multiple integrals, application in finding, mean value of a function of several variables 202
Multiple integrals, application in finding, moments of inertia 201
Multiple integrals, change of variables, double integrals 203—207
Multiple integrals, change of variables, general properties 209—210
Multiple integrals, change of variables, triple integrals 207—209
Multiple integrals, definitions of, double integrals 190—191
Multiple integrals, definitions of, triple integrals 193
Multiple integrals, evaluation 191—193
Multiple integrals, notation 191 192 194
Multiple integrals, order of integration 191—192 194
Multiple integrals, order of integration, caveats 193
Multiplication tables for groups see "Group multiplication tables"
Multiplication theorem see "Parseval's theorem"
Multivalued functions 721—723
Multivalued functions, integration of 762—764
Multivariate distributions 1038 1049—1053
Multivariate distributions, change of variables 1048—1049
Multivariate distributions, Gaussian 1051
Multivariate distributions, multinomial 1050—1051
Mutually exclusive events 962 971
Nabla  see "Gradient operator (grad)" see "Gradient operator (grad)"
Natural logarithm see "ln" "Ln"
Natural numbers, in series 31 124—125
Natural representations 923 952
Necessary and sufficient conditions 34—35
Negative function 583
Negative vector 247
Neumann boundary conditions 635
Neumann boundary conditions, Green's functions 688 700—702
Neumann boundary conditions, method of images 700—702
Neumann boundary conditions, self-consistency 700
Neumann series 872—874
Newton — Raphson (NR) method 1154—1156
Newton — Raphson (NR) method, order of convergence 1157
Neyman — Pearson test 1122
Nodes of oscillation 626
Non-Abelian groups 894—898
Non-Abelian groups, functions 897
Non-Abelian groups, matrices 896
Non-Abelian groups, permutations 898—900
Non-Abelian groups, rotations-reflections 894
Non-Cartesian coordinates see "Curvilinear cylindrical plane "Spherical
Non-linear differential equations see "Ordinary differential equations non-linear"
Non-linear least squares, method of 1118
Norm of function 584
Norm of vector 249
Normal derivative 356
Normal distribution see "Gaussian (normal) distribution"
Normal matrices 277
Normal matrices, eigenvectors and eigenvalues 278—281
Normal matrices, eigenvectors, completeness 280
Normal matrices, eigenvectors, orthogonality 280—281
Normal modes 322—335
Normal modes, characteristic equation 325
Normal modes, coupled pendulums 335 337
Normal modes, definition 326
Normal modes, degeneracy 952—955
Normal modes, frequencies of 325
Normal modes, linear molecular system 326—328
Normal modes, membrane 673 954
Normal modes, normal coordinates 326
Normal modes, normal equations 326
Normal modes, rod-string system 323—326
Normal modes, symmetries of 328
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



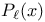 , associated Legendre functions
, associated Legendre functions



 from MGF
from MGF 