|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Riley, Hobson Ч Mathematical Methods for Physics and Engineering |
|
|
 |
| ѕредметный указатель |
Fields, gravitational see "Gravitational fields and potentials"
Fields, scalar 353
Fields, tensor 803
Fields, vector 353
Finite differences 1179Ч1180
Finite differences for differential equations 1180Ч1183
Finite differences from Taylor series 1179 1186
Finite differences, central 1179
Finite differences, forward and backward 1179
Finite differences, schemes for differential equations 1190Ч1192
Finite groups 885
First law of thermodynamics 179
First-order differential equations see "Ordinary differential equations"
Fisher distribution see "F-distribution (Fisher)"
Fisher's Inequality 1075 1076
Fluids, Archimedean up thrust 402 416
Fluids, complex velocity potential 727
Fluids, continuity equation 410
Fluids, cylinder in uniform flow 728
Fluids, flow 727Ч728
Fluids, flux 401 729
Fluids, irrotational flow 359
Fluids, sources and sinks 410Ч411 727
Fluids, stagnation points 727
Fluids, velocity potential 415 612
Fluids, vortex flow 414 728
Forward differences 1179
Fourier cosine transforms 452
Fourier series 421Ч438
Fourier series and separation of variables 652Ч655 657
Fourier series, coefficients 423Ч425 431
Fourier series, complex 430Ч431
Fourier series, differentiation 430
Fourier series, Dirichlet conditions 421Ч422
Fourier series, discontinuous functions 426 428
Fourier series, error term 436Ч437
Fourier series, examples, 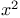 428Ч429 428Ч429
Fourier series, examples, 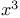 430 430
Fourier series, examples, square-wave 424 425
Fourier series, examples, x 430 431
Fourier series, integration 430
Fourier series, non-periodic functions 428Ч430
Fourier series, orthogonality of terms 423
Fourier series, orthogonality of terms, complex case 431
Fourier series, Parseval's theorem 432Ч433
Fourier series, raison d'etre 421
Fourier series, standard form 423
Fourier series, summation of series 433
Fourier series, symmetry considerations 425 426
Fourier sine transforms 451
Fourier transforms 439Ч459
Fourier transforms as generalisation of Fourier series 439Ч441
Fourier transforms for integral equations 868Ч871
Fourier transforms for PDE 683Ч686
Fourier transforms in higher dimensions 457Ч459
Fourier transforms, convolution 452Ч455
Fourier transforms, convolution theorem 454
Fourier transforms, convolution, and the Dirac  -function 453 -function 453
Fourier transforms, convolution, associativity, commutativity, distributivity 453
Fourier transforms, convolution, definition 453
Fourier transforms, convolution, resolution function 452
Fourier transforms, correlation functions 455Ч457
Fourier transforms, cosine transforms 452
Fourier transforms, deconvolution 455
Fourier transforms, definition 441
Fourier transforms, discrete 468
Fourier transforms, evaluation using convolution theorem 454
Fourier transforms, examples, convolution 454
Fourier transforms, examples, damped harmonic oscillator 457
Fourier transforms, examples, Dirac  -function 449 -function 449
Fourier transforms, examples, exponential decay function 441
Fourier transforms, examples, Gaussian (normal) distribution 441
Fourier transforms, examples, rectangular distribution 448
Fourier transforms, examples, spherically symmetric functions 458
Fourier transforms, examples, two narrow slits 454
Fourier transforms, examples, two wide slits 444 454
Fourier transforms, Fourier-related (conjugate) variables 442
Fourier transforms, inverse, definition 441
Fourier transforms, odd and even functions 451
Fourier transforms, Parseval's theorem 456Ч457
Fourier transforms, properties: differentiation, exponential multiplication, integration, scaling, translation 450
Fourier transforms, relation to Dirac  -function 448 449 -function 448 449
Fourier transforms, sine transforms 451
Fourier's inversion theorem 441
Fraunhofer diffraction 443Ч445
Fraunhofer diffraction, diffraction grating 467
Fraunhofer diffraction, two narrow slits 454
Fraunhofer diffraction, two wide slits 444 454
Fredholm integral equations 864
Fredholm integral equations with separable kernel 866Ч867
Fredholm integral equations, eigenvalues 867
Fredholm integral equations, operator form 865
Fredholm theory 874Ч875
Frenet Ч Serret formulae 349
Frobenius series 545
Fuch's theorem 544
Function of a matrix 260
Functional 835
Functions of a complex variable 711Ч725 747Ч752
Functions of a complex variable, analyticity 712
Functions of a complex variable, behaviour at infinity 725
Functions of a complex variable, branch points 721
Functions of a complex variable, Cauchy Ч Riemann relations 713Ч716
Functions of a complex variable, Cauchy's integrals 745Ч747
Functions of a complex variable, conformal transformations 730Ч738
Functions of a Complex variable, derivative 711
Functions of a complex variable, differentiation 711Ч716
Functions of a complex variable, identity theorem 748
Functions of a complex variable, Laplace equation 715 725
Functions of a complex variable, Laurent expansion 749Ч752
Functions of a complex variable, multivalued and branch cuts 721Ч723 766
Functions of a complex variable, particular functions 718Ч721
Functions of a complex variable, poles 724
Functions of a complex variable, power series 716Ч718
Functions of a complex variable, real and imaginary parts 711 716
Functions of a complex variable, singularities 712 723Ч725
Functions of a complex variable, Taylor expansion 747Ч748
Functions of a complex variable, zeroes 725 754Ч758
Functions of one real variable, decomposition into even and odd functions 422
Functions of one real variable, differentiation of 42Ч51
Functions of one real variable, Fourier series see "Fourier series"
Functions of one real variable, integration of 60Ч73
Functions of one real variable, limits see "Limits"
Functions of one real variable, maxima and minima of 51Ч53
Functions of one real variable, stationary values of 51Ч53
Functions of one real variable, Taylor series see "Taylor series"
Functions of several real variables, chain rule 160Ч161
Functions of several real variables, differentiation of 154Ч182
Functions of several real variables, integration of see "Multiple integrals evaluation"
Functions of several real variables, maxima and minima 165Ч170
Functions of several real variables, points of inflection 165Ч170
Functions of several real variables, rates of change 156Ч158
Functions of several real variables, saddle points 165Ч170
Functions of several real variables, stationary values 165Ч170
Functions of several real variables, Taylor series 163Ч165
Fundamental solution 691Ч693
Fundamental theorem of algebra 86 88 770
Fundamental theorem of calculus 62Ч63
Fundamental theorem of complex numbers see "de Moivre's theorem"
Gamma ,function definition and properties 1201
Gamma function as general factorial function 1202
Gauss Ч Seidel iteration 1160Ч1162
Gauss's theorem 700
Gaussian (normal) distribution 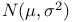 1021Ч1031 1021Ч1031
Gaussian (normal) distribution 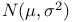 and Binomial distribution 1027 and Binomial distribution 1027
Gaussian (normal) distribution 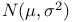 and central limit theorem 1037 and central limit theorem 1037
Gaussian (normal) distribution 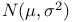 and Poisson distribution 1029Ч1030 and Poisson distribution 1029Ч1030
Gaussian (normal) distribution 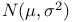 , continuity correction 1028 , continuity correction 1028
Gaussian (normal) distribution 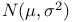 , CPF 1023 , CPF 1023
Gaussian (normal) distribution 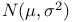 , CPF, tabulation 1024 , CPF, tabulation 1024
| Gaussian (normal) distribution 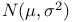 , cumulative probability function 1178 , cumulative probability function 1178
Gaussian (normal) distribution 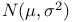 , Fourier transform 441 , Fourier transform 441
Gaussian (normal) distribution 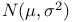 , integration with infinite limits 205 207 , integration with infinite limits 205 207
Gaussian (normal) distribution 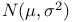 , mean and variance 1022Ч1026 , mean and variance 1022Ч1026
Gaussian (normal) distribution 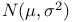 , MGF 1027 1030 , MGF 1027 1030
Gaussian (normal) distribution 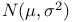 , multiple 1030Ч1031 , multiple 1030Ч1031
Gaussian (normal) distribution 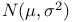 , multivariate 1051 , multivariate 1051
Gaussian (normal) distribution 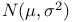 , random number generation 1178 , random number generation 1178
Gaussian (normal) distribution 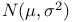 , sigma limits 1025 , sigma limits 1025
Gaussian (normal) distribution 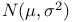 , standard variable 1022 , standard variable 1022
Gaussian elimination with interchange 1159Ч1160
Gaussian integration 1168Ч1170
General Properties see "Anti-Hermitian matrices"
General tensors, algebra 787Ч790
General tensors, contraction 788
General tensors, contravariant 810
General tensors, covariant 810
General tensors, dual 798Ч799
General tensors, metric 806Ч809
General tensors, physical applications 806Ч809 825Ч826
General tensors, pseudotensors 813
General tensors, tensor densities 813
Generalised likelihood ratio 1124
Generating functions, associated Legendre polynomials 594
Generating functions, Bessel functions 573 595
Generating functions, Chebyshev polynomials 597
Generating functions, Hermite polynomials 578 596
Generating functions, Laguerre polynomials 597
Generating functions, Legendre polynomials 562Ч564 594
Generating functions, probability 999Ч1009 see "Probability
Geodesies 825Ч826 831 856
Geometric distribution 1001
Geometric series 120
Gibbs' free energy 181
Gibbs' phenonmenon 427
Gradient of a function of one variable 43
Gradient of a function of several real variables 156Ч158
Gradient of scalar 354Ч358
Gradient of scalar, tensor form 821
Gradient of vector 785 818
Gradient operator (grad) 354
Gradient operator (grad) as integral 404
Gradient operator (grad) in curvilinear coordinates 373
Gradient operator (grad) in cylindrical polars 366
Gradient operator (grad) in spherical polars 368
Gradient operator (grad), tensor form 821
Gram Ч Schmidt orthogonalisation of eigenfunctions of Hermitian operators 589Ч590
Gram Ч Schmidt orthogonalisation of eigenvectors of Hermitian matrices 282
Gram Ч Schmidt orthogonalisation of eigenvectors of normal matrices 280
Gram Ч Schmidt orthogonalisation of functions in a Hilbert space 584Ч586
Gravitational fields and potentials, Laplace equation 612
Gravitational fields and potentials, Newton's law 345
Gravitational fields and potentials, Poisson equation 612 678
Gravitational fields and potentials, uniform disc 706
Gravitational fields and potentials, uniform ring 676
Green's functions 597Ч601 686Ч702
Green's functions and boundary conditions 518 520
Green's functions and Dirac  -function 517 -function 517
Green's functions and partial differential operators 687
Green's functions and Wronskian 533
Green's functions for ODE 188 517Ч522
Green's functions, diffusion equation 684
Green's functions, Dirichlet problems 690Ч699
Green's functions, Neumann problems 700Ч702
Green's functions, particular integrals from 520
Green's functions, Poisson's equation 689
Green's theorems in a plane 390Ч393 413
Green's theorems in three dimensions 408
Green's theorems, applications 639 689 743
Ground-state energy, harmonic oscillator 855
Ground-state energy, hydrogen atom 860
Group multiplication tables 892
Group multiplication tables, order five 904
Group multiplication tables, order four 892 894 903
Group multiplication tables, order six 897 903
Group multiplication tables, order three 904
Grouping terms as a test for convergence 132
Groups, Abelian 886
Groups, associative law 885
Groups, cancellation law 888
Groups, centre 911
Groups, closure 885
Groups, cyclic 903
Groups, definition 885Ч888
Groups, direct product 914
Groups, division axiom 888
Groups, elements 885
Groups, elements, order 889
Groups, examples, 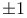 under multiplication 885 under multiplication 885
Groups, examples, alternating 958
Groups, examples, functions 897
Groups, examples, general linear 914
Groups, examples, integers under addition 885
Groups, examples, integers under multiplication (mod N) 891Ч893
Groups, examples, matrices 896
Groups, examples, permutations 898Ч900
Groups, examples, quaternion 915
Groups, examples, rotation matrices 890
Groups, examples, symmetries of an equilateral triangle 889
Groups, finite 885
Groups, identity element 885Ч888
Groups, inverse 885 888
Groups, isomorphic 893
Groups, mappings between 901Ч903
Groups, mappings between, homomorphic 901Ч903
Groups, mappings between, image 901
Groups, mappings between, isomorphic 901
Groups, nomenclature 944Ч945
Groups, non-Abelian 894Ч898
Groups, order 885 923 924 936 939 942
Groups, permutation law 889
Groups, subgroups see "Subgroups"
Hamilton's principle 847
Hamiltonian 855
Hankel transforms 465
Harmonic oscillators, damped 243 457
Harmonic oscillators, ground-state energy 855
Harmonic oscillators, Schroedinger equation 855
Heat flow in bar 656Ч657 683 705
Heat flow in thin sheet 631
Heat flow, diffusion equation 611 629 656
Heaviside function 447
Heaviside function, relation to Dirac  -function 447 -function 447
Heisenberg's uncertainty principle 441Ч443
Helmholtz equation 671Ч676
Helmholtz equation, cylindrical polars 673
Helmholtz equation, plane polars 672Ч673
Helmholtz equation, spherical polars 674Ч676
Helmholtz potential 180
Hemisphere, centre of mass and centroid 198
Hermite equation 541 593 596
Hermite polynomials 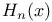 , generating function 578 596 , generating function 578 596
Hermite polynomials 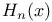 , orthogonality 596 , orthogonality 596
Hermite polynomials 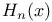 , Rodrigues' formula 596 , Rodrigues' formula 596
Hermitian conjugate 261Ч263
Hermitian conjugate and inner product 263
Hermitian conjugate, product rule 262
Hermitian forms 293Ч297
Hermitian forms, positive definite and semi-definite 295
Hermitian forms, stationary properties of eigenvectors 295Ч296
Hermitian kernel see "Kernel of integral equations Hermitian"
Hermitian matrices 276
Hermitian matrices, eigenvalues 281Ч283
Hermitian matrices, eigenvalues, reality 281Ч282
Hermitian matrices, eigenvectors 281Ч283
Hermitian matrices, eigenvectors, orthogonality 282
Hermitian operators 587Ч591
Hermitian operators in Sturm Ч Liouville equations 591Ч592
Hermitian operators, boundary condition for simple harmonic oscillators 587Ч588
Hermitian operators, eigenfunctions, completeness 588
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



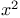
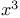
 -function
-function 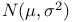
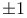 under multiplication
under multiplication 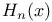 , generating function
, generating function