|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Sutton R.S., Barto A.G. Ч Reinforcement Learning |
|
|
 |
| ѕредметный указатель |
"Steps Toward Artificial Intelligence" paper (Minsky) 18 21 22
 -return 170Ч113 189Ч190 191 198 -return 170Ч113 189Ч190 191 198
 -return algorithm 171Ч112 176Ч180 -return algorithm 171Ч112 176Ч180
Absorbing slate 60
Access-control queuing example 154Ч155 157 160
Accumulating traces or Accumulate-trace methods 173 176 see
Accumulating traces vs. replacing traces 186Ч189 221(fig.)
Acrobot: case study 270Ч274
Action nodes 68
Action preferences 152 185
Action preferences in the n-armed bandit problem 41Ч12 43 44
Action values 69 72Ч14 116
Action values in the n-armed bandit problem 26 27Ч28 48
Action-value functions 69 84 257
Action-value functions and function approximation 210Ч211
Action-value functions and Monte Carlo methods 116Ч118
Action-value functions and TD learning 145Ч146 148 152 154
Action-value functions, optimal 75 78 84
Action-value methods 27Ч30
Actions 51Ч52
Actions in the n-armed bandit problem 26
Actor-critic methods 22 41 151Ч153 159Ч160
Actor-critic methods and Dyna 237(fig.)
Actor-critic methods, eligibility traces for 185Ч186 192
Afterstates 156Ч157
Agent 5 51Ч55
AI see "Artificial intelligence"
Andreae, John 19 84 109
Animal learning psychology see "Psychology and reinforcement learning"
Approximation 80Ч81
Artificial intelligence (AI) 3 5
Artificial intelligence (AI) and DP 109
Artificial intelligence (AI) and reinforcement learning 15 18Ч23 83
Associative learning 18
Associative memory network 225
Associative reinforcement learning 49
Associative reward-penalty algorithm 226
Associative search 45Ч46 49
Asynchronous dynamic programming 103Ч104 107Ч108 110 254
Average-reward case see "Undiscounted continuing tasks"
Averagers 219
Backgammon: program for see "TD-Gammon"
Backup diagrams 71 191
Backup diagrams for DP 70Ч71 76Ч77
Backup diagrams for half-backups 74
Backup diagrams for Monte Carlo methods 115 117
Backup diagrams for n-step TD methods 165
Backup diagrams for one-step methods 243
Backup diagrams for one-step Q-learning 150
Backup diagrams for Q( ) 183 185 ) 183 185
Backup diagrams for Samuel's checker player 269
Backup diagrams for Sarsa( ) 180 ) 180
Backup diagrams for TD( ) 170 ) 170
Backup diagrams for TD(0) 135
Backup diagrams, complex 169
Backups 12 71
Backups in dynamic programming 91
Backups in heuristic search 251Ч253
Backups in Samuel's checker player 268Ч269
Backups, distribution of 195Ч196 201 216Ч218 246Ч249 251 252 254
Backups, full vs. sample 242Ч246
Backups, function approximation and 194Ч195 196 201
Backups, n-step 164Ч165 166 169Ч173
Backups, prioritized sweeping and 239Ч240
Backups, trajectory sampling and 248Ч250
Backward view of eligibility traces 163 175(fig.) 191 192
Backward view of eligibility traces, equivalence with forward view 176Ч179
Backward view of eligibility traces, in Q( ) 182 ) 182
Backward view of eligibility traces, in TD( ) 173Ч178 ) 173Ч178
Backward view of eligibility traces, with function approximation 199 211
Baird's counterexample 216 218 220 224
Bandit problems 48 128 see
Batch updating or Batch training 141Ч144 159
Bellman equations 16 85 90
Bellman equations and backups 108
Bellman equations and DP 101 108
Bellman equations for 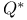 76 76
Bellman equations for 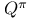 72 72
Bellman equations for 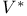 76 76
Bellman equations for 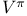 70 70
Bellman equations, solving the 77Ч80
Bellman error 219Ч220 224
Bellman, Richard 16 21 48 49 85 109
Binary bandit tasks 33Ч36 46 49
Binary features 202 205
Binary features vs. radial basis functions 208
Bioreactor: example 54 83
Blackjack: examples 112Ч114 121 131
Blocking maze: example 236Ч237
Boltzmann distribution 30
Bootstrapping 109
Bootstrapping, and DP 109
Bootstrapping, and eligibility traces 220Ч221
Bootstrapping, and function approximation 195 199 201 216Ч222 222Ч223
Bootstrapping, and Monte Carlo methods 115
Bootstrapping, and TD learning 134 138
Bootstrapping, assessment of 139Ч142 220Ч223 224
Boxes 19 131 223
Branching factor 245
Breakfast: example 6Ч7 23
Bucket brigade 159
Car rental: example 98Ч100 157
Cellular telephones: dynamic channel allocation in 279Ч283
Certainty-equivalence estimate 144Ч145 159
Checkers 56 62 251Ч252 267Ч270
Checkers player: Samuel's 109 225 261 267Ч270
Chess 6Ч7 21 56 80 84 156 226
Classical conditioning models 22
Classifier systems 20 22 225
Cliff walking: example 149 150(fig.)
CMAC see "Tile coding"
Coarse coding 202Ч205 208
Complete knowledge 17 82
Complex backups 169
Contingency space 34(fig.) 49
Continuing tasks 58 60Ч61 83
Continuous action 89 153 193 211 226
Continuous state 63 85 89 109 193 202 205 215
Continuous time 52 85 275 276Ч277
Credit assignment 18 163 192
Critic 20 151Ч152 159
Curse of dimensionality 16 107 207
Decision-tree methods 197 226
Delayed reward 4 87 191
Direct reinforcement learning (Direct RL) 230Ч234 254
Dirichlet problem 131
Discount-rate parameter 58 277
Discounting 58Ч59 61 257
Distribution models 227Ч228 244
DP see "Dynamic programming"
Draw poker: example 64Ч65
Driving home: example 135Ч138
Driving: example 55
Dual control 48
Dyna agents 230Ч238 254 258
Dyna agents vs. prioritized sweeping 240Ч241
Dyna agents, architecture 232
Dyna agents, Dyna-AC 257 244
Dyna agents, Dyna-Q 230Ч237
Dyna agents, Dyna-Q+ 237 238
Dyna maze 233Ч235 241
Dynamic channel allocation: in cellular telephone systems 279Ч283
Dynamic programming (DP) 16Ч17 49 89Ч110
Dynamic programming (DP) and artificial intelligence 109
Dynamic programming (DP) vs. Monte Carlo methods 111Ч119 129Ч131 133 256
Dynamic programming (DP), backup diagrams for 70Ч71 76Ч77
Dynamic programming (DP), efficiency of 107Ч108
Dynamic programming (DP), function approximation and 194 216Ч219 222 224 225
Dynamic programming (DP), incremental 109
Dynamic programming (DP), reinforcement learning and 9 16Ч17 23 89 109
| Dynamic programming (DP), temporal-difference learning and 133Ч135 138 159 256
Elevator dispatching: case study 274Ч279
Eligibility traces 163Ч192 see "Replacing
Eligibility traces and Q-learning 182Ч185 192
Eligibility traces and Sarsa 179Ч181 192
Eligibility traces for actor-critic methods 185Ч186 192
Eligibility traces with variable  189Ч190 192 189Ч190 192
Eligibility traces, performance with 221(fig.)
Environment 3 51
Environment and agent 51Ч44
Environment, Markov property and 63
Environment, models of 227
Episodes, episodic tasks 58Ч61 83
Error reduction property 166
Estimator algorithms 48
Evaluation vs. instruction 25 31Ч36
Evaluative feedback 259
Evolution 9 18
Evolutionary methods 9 11 13 20 225 228
Experience 111 228
Experience replay 287
Exploration-exploitation dilemma 4Ч5 130 145 236Ч238
Exploration-exploitation dilemma in the n-armed bandit problem 26Ч27 30 46Ч48 49
Exploratory moves or actions 11 12(fig.) 15 182Ч184
Exploring starts 117 120 122 130
Farley and Clark 18 224
features 200Ч213 225
Forward view of eligibility traces 163 171(fig.) 191
Forward view of eligibility traces in Q( ) 182Ч185 ) 182Ч185
Forward view of eligibility traces in TD( ) 169Ч173 ) 169Ч173
Forward view of eligibility traces with function approximation 198Ч199
Forward view of eligibility traces with variable  190 190
Forward view of eligibility traces, equivalence with backward view 176Ч179 192
full backups 91 108 242Ч246 255Ч256
Function approximation 193Ч225 259
Function approximation, control with 210Ч215
Function approximation, counterexamples to, with off-policy bootstrapping 216Ч220
Function approximation, gradient-descent methods for 197Ч200
Function approximation, linear methods for 200Ч210
Gambler's problem 101Ч103
Gauss Ч Seidel-style algorithm 110
Gazelle calf: example 6Ч7
Generalization 193Ч225
Generalized policy iteration (GPI) 105Ч107 108 210 211 255
Generalized policy iteration (GPI) and Monte Carlo methods 118 122 126 130
Generalized policy iteration (GPI) and TD learning 145 154 157Ч158
Generalized reinforcement 22
Genetic algorithms 8 11 20 48 225
Gibbs distribution 30Ч31
Gittins indices 48 49
Global optimum 196
Goal state 239
goals 4 6 56Ч51
Golf: example 72Ч73 75Ч76 80
GPI see "Generalized policy iteration"
Gradient-descent methods 197Ч201 210Ч213 222 223Ч225
Greedy actions 26
Greedy or e-greedy action selection methods 28Ч30 48
Greedy policies 77 96 119
Greedy policies,  -greedy policies 122 -greedy policies 122
Grid tasks or Gridworld examples, and DP 92Ч94
Grid tasks or Gridworld examples, and eligibility traces 190Ч181
Grid tasks or Gridworld examples, and value functions 71Ч12 78Ч79
Grid tasks or Gridworld examples, cliff walking 149
Grid tasks or Gridworld examples, windy 146Ч148
Hamilton, William 16 84
Hamiton Ч Jacobi Ч Bellman equation 85
Hamming distance 210
Hashing 207 224
Heuristic dynamic programming 109
Heuristic search 250Ч253 256
Heuristic search as expanding Bellman equations 79
Heuristic search as sequence of backups 252Ч253(fig.)
Heuristic search in TD-Gammon 266
Hierarchy and modularity 259
History of reinforcement learning 16Ч23
Holland, John 20 22 48 158Ч159 225
In-place algorithms 91 110
Incomplete knowledge 82
Indirect reinforcement learning 230Ч231 254
Information state 47 49
Instruction vs. evaluation 25 31Ч36
Interaction 6
Interaction, agent-environment 52
Interaction, learning from 3
Interval estimation methods 47 49
Jack's car rental: example 98Ч100 157
Job-shop scheduling: case study 283Ч290
Kanerva coding 209Ч210 224
Klopf, Harry 20Ч22 158 192
Law of effect 17Ч18 49
Learning automata 20 34Ч35 48 49
Learning, and planning 9 227Ч254 259Ч260
Learning, from examples see "Supervised learning"
Learning, from interaction 3 9 13
Least-mean-square (LMS) algorithm 20 223
Linear methods, function approximation using 200Ч210
Linear methods, function approximation using, bound on prediction error 201
Linear methods, function approximation using, convergence of 201 223Ч224
LMS see "Least-mean-square algorithm"
Local optimum 196 198Ч199 201
Lookup tables see "Tabular methods"
Machine learning 3 4 23
Machine learning, special journal issues on reinforcement learning 23
Markov decision processes (MDPs) 16 17 23 66Ч67 82 83Ч84 see "Semi-Markov
Markov property 61Ч65 82 130 258Ч259
Maximum-likelihood estimate 144
Maze examples 233Ч235 236 238 240
MC methods see also "Monte Carlo methods"
MC methods, constant- 134 136 139Ч142 144 171 134 136 139Ч142 144 171
MC methods, every-visit 112 117 131 188
MC methods, first-visit 112Ч113 117 131 188
MDPs see "Markov decision processes"
Mean-squared error (MSE) 195Ч196 201
MENACE (Matchbox Educable Naughts and Crosses Engine) 19 84
Michie, Donald 19Ч20 83 84 131 223
minimax 10 268Ч269
Minsky, Marvin 18 21 22 109
Model-learning 230Ч238 254
Modelfree methods see "Direct RL"
Models (of the environment) 9 82 227Ч228
Models (of the environment) and planning 9 227Ч235
Models (of the environment), incorrect 235Ч238
Models (of the environment), types of 227Ч228
Modified policy iteration 110
Modified Q-learning 159
Monte Carlo methods 111Ч131 see
Monte Carlo methods and control 118Ч121
Monte Carlo methods and DP methods 111Ч112 129Ч131
Monte Carlo methods and TD learning 133Ч145 169 175
Monte Carlo methods, advantages of 129Ч131
Monte Carlo methods, backup diagrams for 115 117
Monte Carlo methods, convergence of 112 120Ч121 124
Monte Carlo methods, eligibility traces and 163 172 188 190Ч191 192
Monte Carlo methods, incremental implementation of 128Ч129
Monte Carlo methods, n-step backups and 164Ч166 170Ч171 172
Monte Carlo methods, off-policy control by 126Ч128
Monte Carlo methods, on-policy control by 122Ч124
Monte Carlo with Exploring Starts (Monte Carlo ES) 120Ч121
Mountain-car task 214Ч215
MSE see "Mean-squared error"
N-armed bandit problem 20 26Ч27 48
N-armed bandit problem, action-value methods and 27Ч31
N-armed bandit problem, associative search and 45Ч46
N-armed bandit problem, evaluation vs. instruction in 31Ч36
N-armed bandit problem, initial action-value estimates and 39Ч41
N-armed bandit problem, Monte Carlo methods and 128
N-armed bandit problem, nonstationary environments and 38Ч39
N-armed bandit problem, pursuit methods for 43Ч45
N-armed bandit problem, reinforcement comparison methods for 41Ч43
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -return
-return 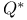
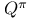
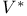
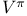
 -greedy policies
-greedy policies 