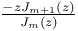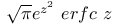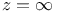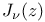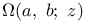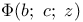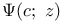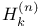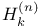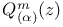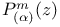|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Джоунс У., Трон В. — Непрерывные дроби. Аналитическая теория и приложения |
|
|
 |
| Предметный указатель |
 -дробь 305 -дробь 305
 -дробь, граница ошибки аппроксимации 306—307 -дробь, граница ошибки аппроксимации 306—307
(M, N)-нормальный ФСР 232
BR-алгоритм см. "Обратный рекуррентный алгоритм"
C-дробь 26 32 137 370
C-дробь правильная модифицированная 321 371
C-дробь, соответствие 161—162
FG-алгоритмы 259—267
FG-алгоритмы вычисления нулей и полюсов функций 265—267
FG-алгоритмы вычисления, последовательного столбцов FG-таблицы 261
FG-алгоритмы вычисления, последовательного строк FG-таблицы 262
FG-таблица 261
FR-алгоритм см. "Прямой рекуррентный алгоритм"
G-дробь 322 373
g-дробь, граница ошибки аппроксимации 306—307
g-дробь, сходимость 146
g-таблица 325
H-дробь 322 371
J-дробь 32 138 236 372
J-дробь, связь с ортогональными полиномами 245—249
J-дробь, связь с присоединенной непрерывной дробью 236—237 244
k-я обращенная разность функции 376
M-дробь 138 374
n-й знаменатель непрерывной дроби 39
n-й числитель непрерывной дроби 39
n-я подходящая дробь 31 37
P-дробь 161 164 194 373
P-дробь, связь с таблицей Поде 194 373—374
P-дробь, соответствие 164
QD-Алгоритм см. "Алгоритм частных и разностей"
QD-схема 224—225
RITZ-дробь 371
S-дробь 137 370
S-дробь модифицированная 321 371
S-дробь, границы ошибки аппроксимации 300—302
S-дробь, представление функции, 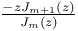 347—348 347—348
S-дробь, представление функции, 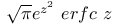 348 348
S-дробь, представление функции, z arc tg z 347
S-дробь, сходимость 144
S-дробь, численная устойчивость BR-алгоритма 346—348
S-дробь, эквивалентные формы 303
SITZ-дробь 371
T-дробь 138 250 251 374
T-дробь соответствующая рациональной функции 363—365
T-дробь, разложение модифицированное функции 362
T-дробь, разложение семейств ограниченных, функций 361—363
Абрамовиц (Abramowitz, M.) 166 171 172 198 214 215 334 382 386
Абсолютная сходимость непрерывной дроби 134
Айне (Ince, E.) 198 252 386
Алгоритм, задающий непрерывную дробь 37
Андерсон (Anderson, Chr.) 231 386
Аппроксимации Ньютона — Паде 196 376
Аппроксимации Паде 35 189
Армс (Arms, R.J.) 35 219 233 234 386
Армса — Эдрея теорема 233—234
Асимптотические разложения непрерывных дробей 325—329
Асимптотическое разложение функции в точке 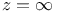 317 317
Асимптотическое разложение функции в точке z=0 320
Аски (Askey, R.A.) 19 198 386
Ахиезер, Н.И. 320 386
Бандемер (Bandemer, H.) 231 386
Банкир (Bankier, J.D.) 63 386
Барнсли (Barnsley, M.) 197 386
Баскервилл (Baskervill, M.) 338 393
Бауэр (Bauer, F.L.) 35 231 236 386
Бейкер (Baker, G.A., Jr.) 17 155 186 197 287 307 308 386 387
Бейтмен (Bateman, H.) 400
Бернулли (Bernoulli, D.) 63 387
Бернштейн (Bernstein, F.) 24 387
Бесселя функция 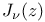 166 166
Бесселя функция 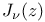 , анализ ошибок аппроксимации 293—294 , анализ ошибок аппроксимации 293—294
Бесселя функция 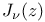 , соответствие непрерывной дроби 166 , соответствие непрерывной дроби 166
Бесселя функция 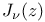 , сходимость 170—171 185 , сходимость 170—171 185
Бета-функция неполная 213—214
Бине функция J(z) 335
Бланш (Blanch, G.) 287 296 338 387
Блюменталь (Blumenthal, O.) 29
Бомбелли (Bombelli, R.) 7 21 387
Борель (Borel, E.) 24 387
Брезински (Brezinski, C.) 17 186 249 387
Броункер (Brouncker, W.) 7 22
Валлис (Wallis, J.) 8 22 23 387
Ван Флек (Van Vleck, E.B.) 29 30 33 76 102 104 125 140 387
Ван Флека теорема 30 102
Варга (Varga, R.S.) 17 186 395
Ватсон (Watson, G.N.) 27 171 387
Ветцел (Wetzel, M.) 29 33 117 125 396
Вещественная J-дробь 138 322 373
Вещественная J-дробь границы ошибки аппроксимации 313—314
Включения область 286—288
Включения область наилучшая 288
Воделанд (Waadeland, H.) 19 36 250 287 316 318 329 361—363 387 390 396
Ворпицкий (Worpitsky, J.) 30 33 76 107 108 387
Ворпицкого теорема 30 107
Вполне положительная последовательность 232
Вуйтак (Wuytack, L.) 17 19 35 186 196 388
Вырожденная гипергеометрическая функция 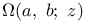 209—210 209—210
Вырожденная гипергеометрическая функция 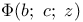 204—205 204—205
Вырожденная гипергеометрическая функция 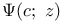 207—208 207—208
Галлучи (Gallucci, M.A.) 196 197 388
Галуа (Galois, E.) 8 23 32 33 63 388
Галуа теоремы обобщение 71—72
Гамма-функция 335—337
Гамма-функция неполная 207 214—215 334
Гаммел (Gammel, J.L.) 17 186 386
Ганкеля определители 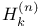 220 220
Ганкеля определители 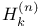 , связь с определителями , связь с определителями  222 222
Ганкеля определители 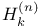 254 254
Гаргантини (Gargantini, I.) 231 388
Гаусс (Gauss, C.F.) 8 11 23 25 26 35 153 388
Гаусса непрерывная дробь 200
Гаучи (Gautschi, W.) 18 19 35 154 167 170 171 198 212—215 243 252 388
Гейне (Heine, H.E.) 8 26
Гершель (Herschel, J.F.W.) 39 388
Гилберт (Gilbert, H.E.) 387
Гилевич (Gilewicz, J.) 17 186 388
Гилл (Gill, J.) 79 287 315 388
Гильберт (Hilbert, D.) 29
Гипергеометрическая функция F(a, b; c; z) 199
Гипергеометрическая функция F(a, b; c; z), представление непрерывной дробью 199—201
Гипергеометрический ряд 25
Глейшер (Glaisher, J.W.L.) 287 315 388
Гранди (Grundy, R.E.) 252 388
Грегг (Gragg, W.B.) 35 186 189 190 194 197 233 242 243 245 287 305—308 389
Грейвс-Моррис (Graves-Morris, P.R.) 17 186 197 387 389
Громмер (Grommer, J.) 29 318 389
Гурвиц (Hurwitz, A.) 24 274 389
Гурвица критерий устойчивости 285
Гурвица полином 274
Гюйгенс (Huygens, Chr.) 8 21—23 389
Гюнтер (Guenther, S.) 63 389
Дарбу (Darboux, J.C.) 8
Двойственная непрерывная дробь 32 72
Двойственная последовательность 72
Двухточечная аппроксимация Паде 197 375
де Брёйн (de Bruin, M.G.) 198 387
Де При (De Pree, J.D.) 79 389
Девис (Davis, P.J.) 249 389
Деннис (Dennis, J.J.) 125 389
Джефферсон (Jefferson, T.H., Jr.) 250 287 304 364 389
Джонсон (Johnson, G.D.) 197 389
Джордан (Jordan, J.Q.) 133 389
Джоунс (Jones, W.B.) 17 29 33 35 36 76 79 84 85 95 108 111 112 116—118 125 133 135 153 183 186 196 197 250 251 255 264—266 287 291 293 294 296 297 300 310 312 318 329 338 340 343 349 353 366 388—390 397
Дисперсионная функция для плазмы 216
Доминирующее решение трехчленных рекуррентных соотношений 167
Донован (Donovan, A.F.) 243 395
Дополнительная функция ошибок 215—216 335
Доу (Dow, J.D.) 197 399
Доусон (Dawson, D.F.) 134 136 390
Доусона интеграл 206 273
| Дробно-линейное преобразование (ДЛП) 31 46
Дробно-линейное преобразование (ДЛП) гиперболическое 68
Дробно-линейное преобразование (ДЛП) двойственное 72
Дробно-линейное преобразование (ДЛП) идемпотентное 85
Дробно-линейное преобразование (ДЛП) локсодромическое 68
Дробно-линейное преобразование (ДЛП) параболического типа 66
Дробно-линейное преобразование (ДЛП) эллиптическое 68
Дробно-линейное преобразование (ДЛП), классификация 65—68
Дрью (Drew, D.M.) 252 390
Задача об очереди 358
Зейдель (Seidel, L.) 30 101 390
Зейделя — Штерна теорема 101
Знаменатель непрерывной дроби n-й 39
Знаменатель непрерывной дроби частный 37
Иенсен (Jensen, J.L.W.V.) 104 390
Измаил (Ismail, M.E.H.) 198 386
Интеграл Доусона 206 273
Интеграл от функции ошибок 215—216
Интегралы Френеля 207 273 382
Интерполяция Эрмита 34 187
Исихара (Isihara, A.) 197 390
Кабаннес (Cabannes, H.) 17 186 390
Казаку (Cazacu, C.A.) 139 390
Каллас (Callas, N.P.) 367 368 390
Каль (Kahl, E.) 63 390
Каратеодори (Caratheodory, C.) 46 390
Карлемана критерий (условие) 302 330
Карлин (Karlin, S.) 349 391
Карлссон (Karlsson, J.) 197 391
Каталди (Cataldi, P.) 21 391
Квадратуры Гаусса 249—250
Кеджори (Cajori, F.) 39 391
Кихара (Chihara, T. S.) 18 249 391
Классенс (Claessens, G.) 19 35 196 197 391
Клаузен (Clausen, Th.) 63 391
Клейн (Klein, F.) 29
Коди (Cody, W.J.) 198 391
Коммон (Common, A.K.) 287 308 391
Конте (Conte, S.D.) 216 398
Копп (Copp, G.) 133 391
Копсон (Copson, E.T.) 166 171 391
Коулинг (Cowling, V.F.) 125 132 391
Кох (von Koch) 135
Коэффициент сходимости 287
Кристоффель (Christoffel, E.B.) 28 391
Кристоффеля числа 249 250
Критические точки 295
Кулона волновая функция 213
Куммера функция 205
Лагерр (Laguerre, E.) 8 26 28 391
Лагранж (Lagrange, J.L.) 8 23 25 391
Ламберт (Lambert, J.H.) 8 25 391
Ланге (Lange, L.J.) 33 125 132 287 311 391 392
Ландсберг (Landsberg, G.) 63 392
Лаплас (Laplace, P.S.) 8 26
Лапласа преобразование 350
Лапласа преобразование обратное 353
Ларкин (Larkin, F.W.) 196 392
Левинсон (Levinson, N.) 274 392
Лежандр (Legendre, A.M.) 8 23 26 392
Лежандра функции второго рода 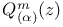 203 203
Лежандра функции второго рода 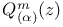 , представление непрерывной дробью 204 , представление непрерывной дробью 204
Лежандра функции первого рода 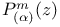 212 212
Лежандра функции первого рода 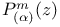 , представление непрерывной дробью 212 , представление непрерывной дробью 212
Лейн (Lane, R.E.) 29 63 83 134 392
Лейтон (Leighton, W.) 18 33 63 91 111 125 132 133 142 161 183 366 386 389 391 392
Лемер (Lehmer, D.H.) 42
Ленер (Lehner, J.) 46 392
Лиувилль (Liouville, J.) 23 392
Локализация особых точек аналитических функций 365—368
Люк (Luke, Y.L.) 198 287 392
Магнус (Magnus, A.) 19 29 36 79 161 194 264—266 349 353 374 389 392
Магнус (Magnus, W.) 400
Мак-Грегор (McGregor, J.L.) 349 391
Мак-Кейб (McCabe, J.H.) 35 138 197 198 251 252 255 259 260 392
Малль (Mall, J.) 104 392
Манделл (Mandell, M.) 79 392
Марков, А.А. 28 330 392
Маркова теорема 250 330—331
Маркушевич, А.И. 46
Маурер (Maurer, G.V.) 198 252 393
Машинная постоянная 340—341
Мейкон (Macon, N.) 338 393
Меркес (Merkes, E.P.) 29 63 287 290 296 369 393 398
Мероморфная в D функция 139
Мероморфная функция 139
Метрическая теория непрерывных дробей 24
Механические квадратуры 25 27
Мёбиуса преобразование 46
Мёрфи (Murphy, J.A.) 35 36 138 197 198 218 251 252 255 259 260 349 360 390 392 393
Миллер (Miller, S.C.) 198 393
Минимальное решение трехчленных рекуррентных соотношений 167 379
Минимальное решение трехчленных рекуррентных соотношений, численная неустойчивость 170—171 379
Модифицированная правильная C-дробь 321 371
Модифицированная правильная S-дробь 321 371
Модифицированное разложение в T-дробь голоморфной функции 362
Моментов проблема в форме Стилтьеса 318
Моментов проблема в форме Стилтьеса сильная 329—331
Моментов проблема в форме Стилтьеса, решение 329—331
Моментов проблема в форме Хамбургера 318—319
Моментов проблема в форме Хамбургера, решение 328—331
Моментов теория 28
Монтессус де Баллор (de Montessus de Ballore, R.) 194 393
Монтессуса де Баллора теорема 194—195
Монтролл (Montroll, E.W.) 197 390
Наилучшая область включения 288
Наилучшая последовательность областей значений 81
Наилучшая последовательность областей элементов 81
Необходимые условия сходимости 93
Неподвижная точка нейтральная 68
Неподвижная точка отталкивающая 68
Неподвижная точка притягивающая 68
Неполная бета-функция 213—214
Неполная гамма-функция 207 214—215 334
Непрерывная дробь бесконечная (неограниченная) 37
Непрерывная дробь двойственная 32 72
Непрерывная дробь конечная (ограниченная) 37
Непрерывная дробь над нормированным полем 41
Непрерывная дробь периодическая 32 63
Непрерывная дробь, значение 39
Непрерывная дробь, определение 37
Непрерывная дробь, сходимость 39
Неравенства фундаментальные 134
Нечетная часть непрерывной дроби 60
Нёрлунд (Noerlund, N.E.) 19 197 393
Норма 41
Нормальная таблица Паде 190
Нормальные аппроксимации Паде 190
Нормальный ФСР 190
Нормированное поле 40
Ньютона — Паде аппроксимации 196 376
Ньютона — Паде аппроксимации нормальные 196
О'Донохоу (O'Donohoe, M.R.) 36 198 218 349 360 393
Оберхеттингер (Oberhettinger, F.) 400
Области сходимости парные 33 см.
Область включения 286—288
Область значений 80
Область сходимости 33
Область сходимости кардиодная 33
Область сходимости круговая приближенная 33
Область сходимости параболическая 33
Область сходимости простая 93
Область сходимости условной простая 94
Область элементов 80
Область элементов параболическая 92
Обратный рекуррентный алгоритм (BR-алгоритм) 45 338—339
Обратный рекуррентный алгоритм (BR-алгоритм) устойчивость 339—341
Общая T-дробь 32 138 251 374
Общая T-дробь, представление функций 268—273
Общая T-дробь, связь с FG-алгоритмом 259—375
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -дробь
-дробь