Авторизация
Поиск по указателям
Oprea J. — Differential Geometry and Its Applications
Обсудите книгу на научном форуме Нашли опечатку?
Название: Differential Geometry and Its ApplicationsАвтор: Oprea J. Аннотация: Differential geometry has a long, wonderful history it has found relevance in areas ranging from machinery design of the classification of four-manifolds to the creation of theories of natures fundamental forces to the study of DNA. This book studies the differential geometry of surfaces with the goal of helping students make the transition from the compartmentalized courses in a standard university curriculum to a type of mathematics that is a unified whole, it mixes geometry, calculus, linear algebra, differential equations, complex variables, the calculus of variations, and notions from the sciences. Differential geometry is not just for mathematics majors, it is also for students in engineering and the sciences. Into the mix of these ideas comes the opportunity to visualize concepts through the use of computer algebra systems such as Maple. The book emphasizes that this visualization goes hand-in-hand with the understanding of the mathematics behind the computer construction. Students will not only see geodesics on surfaces, but they will also see the effect that an abstract result such as the Clairaut relation can have on geodesics. Furthermore, the book shows how the equations of motion of particles constrained to surfaces are actually types of geodesics. Students will also see how particles move under constraints. The book is rich in results and exercises that form a continuous spectrum, from those that depend on calculation to proofs that are quite abstract.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 2nd editionГод издания: 2007Количество страниц: 469Добавлена в каталог: 11.12.2011Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
397 1-forms 430 2-body problem 360 2-cell embedding 291 2-forms 432 2-independent variable EL equation 316 326 2-variable EL equation 315 2-variable first integral 316 Acceleration components 210 Acceleration formulas 125 Acceleration vector 3 Action integral 326 358 Adjoint 193 Adjoint of minimal surface 193 Adjoint to Henneberg's surface 193 Alexandrov's Theorem 176 Almost complex structure J 230 Angle excess theorem 289 301 Arclength 4 214 222 Arclength of geodesic on cone 248 Arclength parametrization 14 Area 414 Area minimization and Maple 203 Area minimization implies minimal 172 416 Area of bugle surface 277 Area of pseudosphere 277 Area of sphere 276 Area of surface 164 276 277 Area of torus 277 Area variation 171 Associated family of minimal surfaces 193 Astroid 10 11 33 Astroid evolute 33 Asymptotic curve 166 Banked highway 29 BAT 207 Bending energy 347 bernoulli 324 Bernoulli's principle 330 Bernstein's theorem 197 Bianchi identity 419 Binormal 19 Bonnet's theorem 304 Bonnet's theorem, converse 305 Book Cover 207 Brachistochrone problem 322 Brachistoclirone 341 Bracket 403 Buckled column 330 Bump lemma 314 Cantilevered beam 332 Catalan's surface 168 Catalan's surface, via Maple 198 Catalan's surface, WE representation 190 Catalan's theorem 167 Catenary 12 13 173 349 Catenary evolute 33 Catenoid 73 120 132 325 370 Catenoid, associated family 193 Catenoid, via Maple 197 201 Catenoid, WE representation 190 Catenoid-helicoid deformation 240 Cauchy - Riemann equations 183 Christoffel symbols 125 409 Christoffel symbols, determined by metric 410 circle 8 14 16 20 24 350 Circle, characterization of 24 Circle, osculating 26 Circular helix 35 36 Clairaut geodesic equations 220 Clairaut parametrization 219 Clairaut relation 218 222 224 225 353 Clairaut relation, on torus 219 Clairaut relation, physical viewpoint 223 Closed 129 Co-state equations 368 369 Codazzi - Mainardi equations 127 Column, buckled 330 Compact 128 complete 225 Complex analytic 182 Complex conjugate 183 Complex differentiable 182 Complex integral 184 Cone 75 117 Cone unrolling 236 Cone unrolling, via Maple 249 Conformal Gauss map 193-195 Conformal map 194 240 241 Conformal metric 227 360 Conformal metric, scaling factor 227 Conformality factor 194 Conjugate point 302 303 344 Connected 69 Connection 1-forms 431 Constant Gauss curvature 112 121 123 Constant Gauss curvature, via Maple 153 Constant mean curvature 112 134 136 137 366 Constant precession curve 21 Constant speed relation 216 Constrained problem 346 347 349 365 382 Contraction 422 Contraction of metric 422 Coordinate chart 397 Covariant derivative 82 278 286 402 423 431 Covariant derivative, properties of 279 402 Cross product 18 CrossProduct 43 Curvature of curve 17 23 29 43 329 347 Curvature of involute 31 Curvature of plane curve 17 Curvature, 2-form 434 Curvature, average normal 109 Curvature, constant Gauss 112 121 123 Curvature, constant mean 112 134 137 Curvature, Einstein 425 Curvature, Gauss 107 109 Curvature, geodesic 210 Curvature, line of 93 Curvature, mean 107 109 181 Curvature, nonnegative Gauss 305 Curvature, normal 92 Curvature, principal 93 109 Curvature, Ricci 420 Curvature, Riemann 417 Curvature, scalar 421 Curvature, sectional 418 Curvature, total Gauss 110 277 Curve 1 Curve of constant precession 21 63 Curve, arclength of 4 Curve, characterization of 38 Curve, closed 38 69 Curve, cusp 3 Curve, differentiable 1 Curve, evolute of 31 Curve, non-unit speed 27 Curve, rectifying 36 Curve, regular 3 Curve, simple 39 Curve, smooth 1 Curve, speed of 3 Curve, torsion of 20 Curve, total torsion of 22 Cycloid 9 51 324 Cylinder 75 94 117 Cylinder unrolling 237 249 Cylinder, twisted 105 Cylindrical helix 34 36 Cylindrical helix, characterization of 34 D'Alembert's principle 223 350 Darboux vector 21 36 Delaunay surface 133 137 365 Delaunay theorem 137 Derivative map 89 Developable surface 117 263 Direction vector 2 Directional derivative 81 Directrix 75 Dirichlet integral 326 Divergence 426 Divergence of metric 426 Divergence of Ricci curvature 427 Dot product 5 DotProduct 43 Double pendulum 363 Doubly ruled 75 Douglas - Rado theorem 171 Eigenvalue 86 Einstein curvature 425 Einstein manifold 428 Elastic rod 348 ellipse 14 16 30 Ellipse evolute 33 Ellipse, arclength of 140 Elliptic E correction xv 145 393 Elliptic functions 138 Elliptic integral 138 Endpoint-curve problem 318 Enneper's surface 74 97 112 170 Enneper's surface, via Maple 198 Enneper's surface, WE representation 191 Euler - Lagrange equation 314-316 319 328 347 355 358 367 380 412 Euler characteristic 291 292 Euler's formula 96 Euler's spiral 38 348 Evolute 31 48 Evolute of astroid 33 49 Evolute of catenary 33 49 Evolute of ellipse 33 48 Evolute of parabola 32 Exterior derivative 432 Extremal 315 334 356 Extremize 315 356 Fermat's principle 324 Feynman quote 284 Field of extremals 334 345 Final time fixed 317 First Bianchi identity 419 First integral 316 358 381 First structure equation 432 Fixed endpoint problem 312 316 341 Flat 417 Flat surface 110 Flat surface of revolution 133 Flat surfaces of revolution via Maple 201 Flat torus 229 230 Foucault pendulum 284 Foucault vector field 285 Frame 278 Frame field 278 420 434 Frenet formulas 20 28 Frenet frame 19 fundamental frequency 365 Fundamental theorem of space curves 38 Gauss - Bonnet theorem 291 Gauss curvature 107 109 227 418 434 Gauss curvature of 114 126 Gauss curvature of Enneper's surface 114 Gauss curvature of minimal surface 193 Gauss curvature of surface of revolution 119 121 Gauss curvature, depends only on metric 124 Gauss curvature, nonnegative 305 Gauss curvature, sign of 108 Gauss curvature, via Maple 150 Gauss map 90 110 193 194 Gauss map, area of 110 Gauss map, for catenoid 91 Gauss map, for cone 90 Gauss map, for cylinder 90 Gauss map, for Enneper 91 Gauss map, from WE representation 195 Gauss's lemma 298 Geodesic 212 238 352 356 369 411 Geodesic constant speed relation 216 Geodesic curvature 210 231 281 358 Geodesic curvature, depends only on metric 211 Geodesic equations 216 369 413 Geodesic equations, Clairaut 220 Geodesic equations, via Maple 242 Geodesic has constant speed 212 Geodesic in conformal metric 256 Geodesic on cone 222 Geodesic on cone, via Maple 247 Geodesic on cylinder 214 216 Geodesic on hyperbolic plane 233 239 Geodesic on hyperboloid of 1-sheet 225 293 Geodesic on paraboloid 224 Geodesic on plane 222 Geodesic on Poincare plane 232 Geodesic on sphere 213 216 Geodesic on sphere, via Frenet formulas 214 Geodesic on stereographic plane 234 256 Geodesic on stereographic sphere 234 Geodesic on surface of revolution 221 Geodesic on torus 218 Geodesic on unduloid 251 Geodesic on whirling witch of Agnesi 222 Geodesic parameter curve 221 Geodesic plane curves 216 Geodesic polar coordinates 214 297 Geodesic torsion 281 282 Geodesic via Maple 243 Geodesic, as length minimizer 214 Geodesic, as line of curvature 214 Geodesic, existence of 216 Geodesically complete 225 Geodesics 353 Geographical coordinates 70 Goldschmidt discontinuous solution 173 Great circle 213 Green's theorem 39 287 Hadamard's Theorem 296 Hamilton's principle 312 326 Hamiltonian 368 369 Harmonic conjugate 183 Harmonic function 179 Helicoid 74 75 116 166 Helicoid isometry 236 Helicoid, WE representation 190 Helicoid-catenoid animation 199 Helix 11 16 44 Helix, circular 35 56 Helix, curvature of 22 Helix, cylindrical 34 Helix, hyperbolic 31 Helix, involute of 17 Henneberg's surface 168 Henneberg's surface adjoint 193 Henneberg's surface, WE representation 191 Higher-order Euler - Lagrange equation 329 Hilbert's invariant integral 337 Hilbert's Lemma 132 Holomorphic 182 Holonomic constraints 350 Holonomy 281 283 Holonomy, as total Gauss curvature 288 Holonomy, on cone 284 308 Holonomy, on Poincar 287 Holonomy, on sphere 282
Реклама
-patch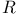 
-sphere 
plane 
|
|
О проекте