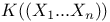|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Jensen C.U., Lenzing H. — Model Theoretic Algebra with particular emphasis on Fields, Rings, Modules |
|
|
 |
| Предметный указатель |
 -simple 199 -simple 199
 -algebraically compact indecompos-able module 245 -algebraically compact indecompos-able module 245
 -algebraically compact module 160—161 163—164 169—171 193—195 216 245 -algebraically compact module 160—161 163—164 169—171 193—195 216 245
 -algebraically compact ring 281 -algebraically compact ring 281
 -injective module 122 239 245 -injective module 122 239 245
 -pure-injective module 161 -pure-injective module 161
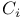 -field 19 30—32 -field 19 30—32
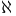 -coherent ring 142 152 142 -coherent ring 142 152 142
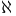 -compact module 144 146 155 141 -compact module 144 146 155 141
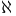 -complete filter 140 152 -complete filter 140 152
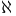 -generated module 136 -generated module 136
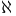 -injective functor 142—144 150—151 -injective functor 142—144 150—151
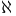 -injective module 141 -injective module 141
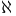 -presented module 136 -presented module 136
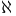 -projective module 152 -projective module 152
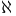 -pure-exact sequence 139 -pure-exact sequence 139
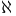 -pure-injective module 141 -pure-injective module 141
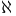 -saturated 12 -saturated 12
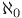 -compact module 157 -compact module 157
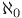 -complete ultrafilter 156 -complete ultrafilter 156
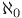 -incomplete ultrafilter 156 -incomplete ultrafilter 156
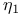 -ordered field 23 41 43 -ordered field 23 41 43
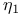 -set 23 173 -set 23 173
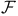 -product 140 -product 140
(m,n)-presented module 228
Abelian category 381
Absolutely irreducible polynomial 6
Absolutely pure module 577
Additive category 379
Additive functor 319
Adic completion 118 190
Adic topology 118
Admissible field 77
Affine algebraic group 312
Affine group scheme 315
Affine k-algebra 310
Affine n-space 310
Affine scheme 313
Affine scheme, defined over the integers 316
Affine variety 310
Affine variety of modules 317
Algebraic compactness, of reduced power 154
Algebraic compactness, of ultrapower 287
Algebraic compactness, of ultraproduct 293
Algebraic number field 13 24 29
Algebraically closed field 5 13 16—17 19—21 23 30—31 40 43 49 58—59 306 309
Algebraically closed relatively 4
Algebraically compact module 125 128 130—131 144 154 157 165 171
Algebraically compact module, indecomposable 159 126 375
Algebraically compact module, over a Dedekind domain 205
Algebraically compact ring 281 285 287—288 323
Almost all 2
Almost-disjoint 195 175
Almost-split sequence 332
Amitsur's theorem 273
Amitsur-Levitzki's theorem 273
Anderson, F. W. 234 247
Annihilator of subfunctor 132
Archimedean field 41 48
Aronszajn, N. 207—208
Artin algebra 325 401
Artin-Schreier's theorem 21—23
Artinian module 401
Artinian ring 226 232 234—237 241 245 401
Atomic formula 307
Auslander's test 331
Auslander, M. 166 336 356
Auslander-Reiten quiver 336
Auslander-Reiten translate 333
Automorphism group of field 63
Ax and Kochen's theorem 31 69
Ax, J. 31 37 57
Ax-Kochen's theorem 31 60
Axiomatizability for Artinian rings 226 250
Axiomatizability for Ci-fields 32
Axiomatizability, for finite dimensional algebras 325
Axiomatizability, for finitistic projective dimension 263
Axiomatizability, for flat modules of rank n 244
Axiomatizability, for fp-injective modules 239
Axiomatizability, for fp-self-injective rings 278
Axiomatizability, for global dimension 262
Axiomatizability, for Goldie dimension 238
Axiomatizability, for infinite projective dimension 235
Axiomatizability, for infinite representation type 339
Axiomatizability, for n -generated flat modules 244
Axiomatizability, for self-injective dimension 278
Axiomatizability, for semifirs 256—257
Axiomatizability, for semihereditary rings 256—257
Axiomatizability, for semiperfect rings 252
Axiomatizability, for semiprimary rings 252
Axiomatizability, for uniformly coherent rings 254
Axiomatizability, for universally admissible fields 79
Axiomatizability, for weak global dimension 258—259
Axiomatizability, for weak global dimension one 256—257
Axiomatizable class 15—16 32
Axiomatizable class, of 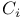 -fields 19 -fields 19
Axiomatizable class, of algebraically closed fields 17
Axiomatizable class, of fields of characteristic zero 16
Axiomatizable class, of fields with trivial Brauer group 20
Axiomatizable class, of flat modules 122
Axiomatizable class, of formally real fields 21
Axiomatizable class, of Hilbertian fields 75
Axiomatizable class, of injective modules 122
Axiomatizable class, of Peano fields 61
Axiomatizable class, of Peano rings 61
Axiomatizable class, of projective modules 122
Axiomatizable class, of real closed fields 22
Axiomatizable class, of separably closed fields 17
Back-and-forth construction 39
Baer's test for injectivity 239 368
Baer, D. 126 163 209 245 293 297 299 356
Baer, R. 239 368
Barwise, J. 1 11 39 69 156—157 172 309
Base change 316
Bass's theorem 165—166 332
Bass, H. 122 165 232 234 251—252 263 271
Baur, W. 91—92 100 158 219
Bautista, R. 340—341
Bauval, A. 68 268
Bell, J. L. 1 5 12 16 20 61 159
Bergman, G. 268
Bernstein, I. N. 169 207
Bezout Domain 119 249 279 401
Bjork, J. -E. 251
Bongartz, K. 340 342
Boolean algebra free 261
Bound for coherence 229—230 232 254
Bounded representation type 165
Bourbaki, N. 52 114—115 229 231 257 305
Brauer group 20
Brauer group, trivial 20
Brauer-Thrall conjecture first 166
Brune, H. 291 297 299 356
Cancellation law, for function fields 30 35 57—58 70
Cancellation law, for polynomial rings 34 71 259 262
Cancellation law, for power series fields 30 56
Cancellation law, for power series rings 269—270 278
Cartan, H. 123 231 234 256
Cassels, J. W. S. 25—26 28
Category, abelian 381
Category, additive 379
Category, of additive functors 384
Category, path 405
Chang, C. C. 1 11—12 15 24 31 46 57 69
Characteristic transfer principle 6
Chase, S. U. 122 163 229 260
Cherlin, G. L. 23
Chevalley's Theorem 311 317
Chevalley, C. 313
Class, axiomatizable 15—16
| Class, elementarily closed 13
Class, finitely axiomatizable 15
Closed subscheme 314 345
Cogenerator 401
Cohen, I. S. 232
Coherent module 237
Coherent ring 97 99 106 108 122 124 229 231—232 236—237 253 255 258—259 264—265 278—279 377 401
Cohn, P. M. 184 257
Colliot-Thelene, J. L. 28
Commutative Noetherian ring 113 115—122
Compact module 158
Compactness Theorem 3 16
Complete local ring 56
Completion-adic 29 59
Complex number field 23
Constructible set 311
Constructible subscheme 315 342
Continuum Hypothesis 24 172 293—294
Continuum hypothesis, generalized 12
Coordinate algebra 310
Coordinate ring 313
Countable ring 157 235—236 239
Crawley-Johnsson-Warfield theorem 234
Cubically closed field 55
Curtis, C. W. 324
Cyclically presented module 97
Dedekind domain 98 109 115 168 170 182 190 201 216 218 232 250—251 265 291 402
Dedekind, R. 249
Definable subfunctor 135
Definable subgroup 125 161 171
Delon, F. 57 60 74
Demazure, M. 313
Dense functor 380
Descending chain condition, for closed subsets 311
Descending chain condition, for submodules 401
Descending chain condition, on finitely generated ideals 251
Descending chain condition, on principal ideals 235 251
Descent infinite 35 51
Diagonal embedding 2 4
Diagonal mapping 2 125
Diagram, expansion 308
Diagram, language 308
Dieudonne, J. 207
Dimension, embedding 265
Dimension, finitistic global 313
Dimension, flat 369
Dimension, fp-injective 264 377
Dimension, Gelfand-Kirillov 275 277—278
Dimension, global 278 369
Dimension, Goldie 238
Dimension, injective 369
Dimension, Krull 117—118 121 123 254 271 276—278 313 378
Dimension, local 313
Dimension, of topological'space 272
Dimension, projective 234 369
Dimension, pure-global 155 291—292 375
Dimension, pure-injective 155 375
Dimension, pure-projective 291—292
Dimension, weak global 370
Dimension, weak homological 231 369
Discrete valuation ring 56
Dlab, V. 209
Domain, factorial 50 378
Domain, principal ideal 406
Domanov, O. I. 268
Douady, A. 77
Dries, L. van den 29 77 307
Dugas, M. 63
Dynkin diagram 169
Eakin, P. 270
Eilenberg, S. 123 231 234 256
Eklof, P. C. 37 122
Elementarily closed class 13
Elementarily closed class, of algebraically closed fields 13
Elementarily closed class, of flat modules 122
Elementarily closed class, of projective modules 122
Elementary class of representation-finite rings 301
Elementary definability 33
Elementary definability, in field of quotients 61—62
Elementary definability, in number field 66
Elementary definability, of ![$K[[{X}_{1},...,{X}_{n}]]\;in\;K\;(({X}_{1},...,{X}_{n}))$](/math_tex/e583579c6ee1e8f6ddaba56e43d4b92d82.gif) 50 50
Elementary definability, of field in function field 34
Elementary definability, of Henselian ring in quotient field 50 56
Elementary definability, of integers in polynomial ring 36
Elementary definability, of Q in polynomial ring 36
Elementary definability, of ring in field of quotients 56
Elementary descent 229—230 235 237 240 244
Elementary descent, for  -algebraically compact modules 239 -algebraically compact modules 239
Elementary descent, for  -algebraically compact rings 287 -algebraically compact rings 287
Elementary descent, for  -injective modules 239 -injective modules 239
Elementary descent, for algebraically compact modules 239
Elementary descent, for algebraically compact rings 285
Elementary descent, for Artinian modules 237
Elementary descent, for Artinian rings 237
Elementary descent, for coherent rings 255
Elementary descent, for Dedekind domains 251
Elementary descent, for flat modules 229
Elementary descent, for free modules 235
Elementary descent, for GK-dimension 276—277
Elementary descent, for global dimension 260 262
Elementary descent, for injective modules 239—240
Elementary descent, for Krull dimension 276
Elementary descent, for locally coherent modules 237
Elementary descent, for locally coherent rings 237
Elementary descent, for maximum condition 244
Elementary descent, for minimum condition 244
Elementary descent, for Noetherian modules 237
Elementary descent, for Noetherian rings 237 251
Elementary descent, for perfect rings 253
Elementary descent, for primitive rings 268
Elementary descent, for principal ideal domains 251
Elementary descent, for projective modules 235
Elementary descent, for pure-projective modules 235
Elementary descent, for regular local rings 262
Elementary descent, for transcendency degree 277
Elementary descent, for weak global dimension 259
Elementary embedding 4
Elementary equivalence 11 15
Elementary equivalence of fields 32
Elementary equivalence of Henselian fields 31
Elementary equivalence of power series fields 31
Elementary equivalence, for algebraically closed fields 5
Elementary equivalence, for embedding dimension 266
Elementary equivalence, for fields 13—14
Elementary equivalence, for flat modules 106 115—119 229
Elementary equivalence, for fp-injective dimension 240
Elementary equivalence, for fp-injective modules 108
Elementary equivalence, for fp-self-injective rings 265
Elementary equivalence, for free algebras 266
Elementary equivalence, for function fields 14 28 30 43 47—49 57—58 70
Elementary equivalence, for global dimension 261
Elementary equivalence, for injective dimension 240
Elementary equivalence, for injective modules 120
Elementary equivalence, for injective modules over commutative Noetherian rings 121
Elementary equivalence, for Krull dimension 276
Elementary equivalence, for localizations 112—113
Elementary equivalence, for matrix rings 238 274
Elementary equivalence, for modules over Z[X] 115
Elementary equivalence, for Noetherian rings 251
Elementary equivalence, for number fields 13
Elementary equivalence, for polynomial rings 36—37 39 43 71 259 262
Elementary equivalence, for power series fields 31 56—57
Elementary equivalence, for power series fields 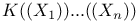 30 30
Elementary equivalence, for power series fields 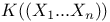 31 31
Elementary equivalence, for power series rings 43 269—270 278
Elementary equivalence, for R-modules 100 107
Elementary equivalence, for rational function fields 28
Elementary equivalence, for real closed fields 9 23 41—42
Elementary equivalence, for rings of continuous functions 272
Elementary equivalence, for self-injective rings 265
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -simple
-simple  -algebraically compact indecompos-able module
-algebraically compact indecompos-able module 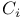 -field
-field 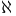 -coherent ring
-coherent ring 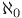 -compact module
-compact module 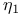 -ordered field
-ordered field 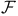 -product
-product ![$K[[{X}_{1},...,{X}_{n}]]\;in\;K\;(({X}_{1},...,{X}_{n}))$](/math_tex/e583579c6ee1e8f6ddaba56e43d4b92d82.gif)