|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Chvatal V. — Linear programming |
|
|
 |
| Предметный указатель |
Farm planning example 177—182
Feasible dictionary 19
Feasible flow 370
Feasible origin 28
Feasible region see "Region of feasibility"
Feasible solution 6
Feasible tree solution 296 354
Feinstein, A. 371
Fermat, P. 251
Fiala, F. xiii
File, backward 408
File, eta 110—112
File, forward 408
Fill-in 78 409—410
Finals 195
Finite basis theorem 244
Finite Basis Theorem, converse of 245
First-fit decreasing (FFD) 208
First-labeled, first-scanned 380
Floating-point arithmetic 74
Flow 369
Flow problems see "Upper-bounded transshipment problems"
Flow, blocking 383
Flow, feassible 370
Flow, volume of 370
Ford, L. R. Jr. 367 371 374 378 390 391
Forestry, case study in 171—176
Forrest — Tomlin method 410—412
Forrest, J. J. H. 406 410—411
Forsythe, G. 77
Forward arc 300 361
Forward error analysis 75
Forward file 408
Forward transformation (FTRAN) 111 114 406
Fourier — Motzkin method 241—242
Fourier, J. B. J. 8 227 241—242 254
Fox, K. 171 177
Free variable 119 132—133 138
Free variable, treatment of 132—133
Fulkerson, D. R. 339 341 367 371 374 390 391 435
Full row rank 133 227
Function, linear 6
Function, objective 6
Fundamental Theorem of Linear Programming 42 133—134
Gacs, P. xiii 451
Gaddum, J. W. 324
Gale, D. 57 68 228 273 364 366
Galil, Z. 380
Galileo, G. 251
Game of Cheap, Middling or Dear 239
Game of Morra 228—230 232 237 238
Game of poker 235—237 238—239
Game theory 228—239
Game theory, equivalence with linear programming 232 239
Game, fair 233
Game, matrix 230
Game, symmetric 233
Game, value of 233
Gantmacher, F. R. 444
Garey, M. R. 51 336
Garfinkel, R. S. 207
Gasoline blending example 10—11 69 70
Gass, S. I. 9 163
Gassner, B. J. 303
Gauss — Jordan elimination xii 79
Gauss, C. F. 74 227
Gaussian distribution 220
Gaussian elimination xii 71—79 272 277 443—444
Gaussian elimination, accuracy of 74—77
Gaussian elimination, matrix description of 84—88
Gaussian elimination, speed of 77—78
Gay, D. M. 414
General form of linear programming problems 119 137—138
Generalized upper bounding (GUB) 415—424
Geometric interpretation of the simplex method 253—255
Gilmore, P. C. 198 206 209—211
Givens, W. 75
Glassey, C. R. 347
Glover, F. 391
Goldfarb, D. 115 457
Goldstine, H. H. 75
Golub, G. H. 406
Gomory, R. E. 198 206 209—211
Goodness of fit 213 216—221
Gordan, P. 248
Graph 331
Graph, bipartite 332 372 388
Graphic method x 260—261
Grattan-Guiness, I. 227
Greene, J. H. 10
Groetschel, M. 451
Gruenbaum, B. 267
Gupta, V. K. 347
Hahn, G. xiii
Half-ellipsoid 446
Half-simplex 452
Half-space 252
Hall's theorem 337
Hall, P. 337
Halmos, P. ix
Hammersley, J. M. 330
Hanssmann, F. 193
Harris, P. M. J. 115
Hashing tables 282
Hawkins, T. 81
Head of an arc 292
Heap 402
Hellerman — Rarick procedure 91—92
Hellerman, E. 91
Helly, E. 266
Hess, S. W. 193
Heuristic, FIRST-FIT DECREASING 208
Higham, P. xiii
Hirshfeld, D. M. 416
History of linear programming 7—9
Hitchcock transportation problem 345
Hitchcock, F. L. 345
Ho, J. K. 194 441
Hochbaum, D. xiii
Hoffman, A. J. xiii 33 193 330
Hopcroft, J. E. 282
Hotelling, H. 75
Hull see "Convex hull"
Hungarian method: Primal-dual method (so named by H. W. Kuhn in recognition of work, by J. Egervary and D. Koenig) see "Assigment problem"
I-Ching 74
Identity matrix 81
implementations see "Computer implementations"
Incidence matrix of a network 294
Incidence matrix of a network, truncated 295
Incoming variable see "Entering variable"
Incomplete information at the center 436
Inconsistent system of linear inequalities 144
Inequality constraints in transshipment problems 320—322
Inequality, linear 6
Inequality, redundant 242 247
Infeasibility form 129
Infeasible, linear programming problem 7 143
Infeasible, upper-bounded transshipment problem 364
Initialization of the Dantzig — Wolfe decomposition algorithm 432—434
Initialization of the network simplex method 303—306
Initialization of the primal-dual method 393 398—399
Initialization of the simplex method 42 125—129
Inner product see "Scalar product"
Integer linear programming problems (ILP problems) 328
Integral flow theorem 371
Integrality theorem 327 365
Intermediate node 292 369
Inventory scheduling 188—193 322—323
Inverse of a matrix xii 94
Inverse of the basis xi 117
| Inverse of the basis in the product form xi 105 117
Ishii, M. xiii
Iterations, number of in the Dantzig — Wolfe decomposition algorithm 441
Iterations, number of in the network simplex method 311 335
Iterations, number of in the primal-dual method 398 400
Iterations, number of in the simplex method 45—51
Jacobs, W. 193 324
Jeroslow, R. G. 50
Jewell, W. S. 435
Johnson, D. B. 392
Johnson, D. S. 51 208 336
Join 309
Jordan, W. 79
Judin, D. B. 9 451
k-heap 402
Kantorovich, L. V. 8
Karp, R. M. 380 391 400
Kepler, J. 251
Khachian, L. G. 9 52 444 451
Kirchberger, P. 267 269
Kirchhof's law see "Conversation law"
Klee — Minty problems 47—49 53 255—258
Klee, V. xiii 47 267
Klincewicz, J. G. 303
Knapsack problem 200—207
Knuth, D. E. 282
Koenig — Egervary theorem 334
Koenig's Theorem 328
Koenig, D. 328 330 334
Kohler, D. A. 241 254
Koopmans, T. C. 8
Kotiah, T. C. T. 33
Kotzig, A. 371
Kubat, P. xiii
Kuhn's simplified poker 235—237 238—239
Kuhn, H. W. xiii 43 46 57 144 228 235 238 242 374 390 400
Labeling method see "Augmenting path method"
Landau, H. G. 366
Laplace, P. S. 227
Large-scale problems 113 416
Largest-coefficient rule 46 50
Largest-increase rule 50
Lau, H. T. xiii
Lawler, E. L. 336
Layered network see "Core "in Dinic's algorithm)
Least squares approximation (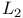 approximation) see " approximation) see "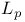 -approximation" -approximation"
Leaving arc 300
Leaving column 102
Leaving variable 21 29 123 124
Legendre, A. M. 74 227
Leibniz, G. W. 251
Lemke, C. E. 152
Length of a path 391
Length of a vector 82
Levin, A. Ju. 451 452
Levin, L. A. xiii 452
Lexicographic method 34—37
Linder, R. E. 214
Line 276
linear combination 55 138
Linear constraints 6
Linear equation 6
Linear equation, systems of 71—79 82 93—94 272 443—444
Linear function 6
Linear graph see "Graph"
Linear inequality 6
Linear inequality, strict 43 448—451
Linear inequality, systems of 143—146 240—249 444—454
Linking constraints 435
Logical variable see "Artifical variable; Slack variable"
Loute, E. 441
Lovasz, L. 451
Lower triangular matrix 83
Lower-bounds on individual variables 119
LU-Decomposition 88
M Method see "Big M method"
MacLagan, R. C. 239
Magee, J. R. 193
Maheshwari, S. N. 384
Malhotra — Kumar — Maheshwari procedure 384—386 388 389
Malhotra, V. M. 384
Mandelbrot, B. 221
Manne, A. S. 194
Marginal value 66 see
Markowitz's pivoting strategy 89
Markowitz, H. M. 78
Marriage theorem see "Koenig's Theorem"
Marshall, K. T. 33
Martin, M. S. xiii
Master problem 426 440—441
Masuda, S. 12
Matching 331 372
Matrix 81—84 92—94
Matrix description of dictionaries 98—100
Matrix game 230 see
Matrix representation of systems of linear equations 82
Matrix, algebra of matrices 84
Matrix, basis matrix 100
Matrix, block-angular 434—435
Matrix, block-diagonal 435
Matrix, block-triangular 412
Matrix, doubly stochastic 329
Matrix, entry of 81
Matrix, eta 83
Matrix, identity 81
Matrix, incidence 294
Matrix, inverse of 94
Matrix, lower triangular 83
Matrix, node-arc see "Matrix incidence"
Matrix, nonsingular 93
Matrix, operations on 79—82 84
Matrix, packed 82—83
Matrix, payoff 230
Matrix, permutation 83 86—87 90—91 406—407
Matrix, product 81
Matrix, regular see "Matrix nonsingular"
Matrix, singular 93
Matrix, sparse 82
Matrix, storing 82—83
Matrix, sum 84
Matrix, transpose of 84
Matrix, triangular 83
Matrix, truncated incidence 295
Matrix, upper-triangular 83
Matrix, zero-one 366
Mattheis, T. H. 282
Mauldon, J. C. 330
Max-flow min-cut theorem 370
Maximum-flow problem 370
Maximum-flow problem, applications of 372—373
McMullen, P. 272—273
Mean 219
Meat-packing example 10 69 70 352
Median 219
Median method 210
Memory of a computer 113—115 406 408
Merrill, A. L. 184
Midrange 219
Mill, J. S. 251
Minimax theorem 233 234 239
Minimum cost network flow problem see "Upper-bounded transshipment problems"
Minimum cut see "Max-flow Min-cut Theorem"
Minkowski — Farkas lemma see "Farkas's lemma"
Minkowski, H. 245 262
Minty, G. J. 47
Mixed strategy 231
Models of economy 68
Molecular absorptivity 214
Moler, C. 77
Morra 288—230 232 233 237 238
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



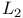 approximation)
approximation) 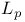 -approximation"
-approximation"