|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dauns J. Ч A Concrete Approach to Division Rings |
|
|
 |
| ѕредметный указатель |
A.C.C. = ascending chain condition 296
Albert, A.A. xii xvi 30 32 35 42 46 118 120Ч124 128 129Ч131 294 316 323Ч324 327 333 339
Algebraic closed field 117 182
Algebraic closed ring 366 370
Algebraic extension 60 99 117 213
Algebraic number field 32 117
Alternative ring 334Ч335
Amitsur Ч Levitsky theorem 160
Amitsur, S.A. xiii 32 133 135 153 164Ч165
Amitsur, S.A. and Saltman, D. 124
Anti-automorphism 4
Anti-homomorphism 4
Anti-isomorphism 4
Artin, E. xiv 44 47 56 60 170 327
Artin, E. and Nesbitt, C.J. and Thrall, R. 25 33 82 84 87 97 98 116Ч117
Associates 347
atom 345 364
Automorphism 27 222
Automorphism, extension 36 179
Automorphism, inner 37 84 96Ч98 175Ч176 180 229 231 232
Behrend, F. 333
Benard, M. 153
Benard, M. and Schacher, M. 153
Bezout, right 350
Bezout, weak domain 351Ч354 356
Bilinear inner product 337
Binomial extension 245 264 285Ч286 288
Birkhoff, G. and von Neumann, J. 333
Blaschke, W. xii
Bokut, L.A. xv
Bott, R. and Milnor, J. 333
Bowtell, A.J. xv
Brauer group 114Ч115 152
Brauer, R. xii 32 114Ч115 123Ч124 152
Bruck, R.H. 342
Caley Ч Dickson algebra 338
Caley Ч Dickson process 338Ч339
Cancellative semigroup 297
Cayley algebra 333 337Ч339
Cayley, A. xi
Cecioni, F. 123
Center nonassociative ring 334
Center ring 102 159 232 235
Central polynomial 155
Central simple algebra 33 93 95 97
centralizer 322 362Ч363
Centrally finite division algebra 30
Change of coordinates 219Ч222
Cohn, P.M. xiii xvЧxvi 184 221 238 240Ч241 263 271 312 319 347 351 356 362Ч363
Commutation polynomials 268
Commutator element 218
Commutator ring, A-commutator 46 97Ч98
Commutator ring, D-commutator 76
Commutator ring, R-commutator 93
Conjugate element 19
Conjugate roots 361 363
Conrad, P. 295 305 316
Conrad, P. and Dauns, J. 294
Conway, A.W. xii
Coprime 346
Coxeter, H.S.M. xii
Cozzens, J.H. 370
Cozzens, J.H. and Faith, C. 224
Crossed product 58 61 64Ч65 67 83 85 103 138Ч153 see "Wedderburn
Crossed product, cyclic 71
Crossed product, cyclic division ring 86 119Ч122
Crossed product, noncyclic 124 182
Cyclic algebra 46 71Ч73 86Ч87 176
Cyclic division ring 58 119
Cyclic field 45 121
D.C.C. = descending chain condition 94 98
Dauns, J. 295 305 309 312 352
Deavours, C.A. xii
Degree of algebra 116Ч117 124
Derivation 189 218 333 see "Lie
Derivation, (S,T)-derivation 270Ч274
Derivation, inner 194 270Ч271 284 287 288
Derivation, inner right 194 271
Derivation, left 189
Derivation, nilpotent 275Ч293
Derivation, outer 194
Derivation, right 189 265 267 275 284
Derivation, surjective 218
Deuring, M. xvi 4
Dickson, L.E. xiЧxiii xvi 32 51 123 131
Differential basis 277 286 289 292Ч293
Differential polynomial 223
Differentially closed 370
Dimension finite 366
Dirac, P.A.M. xii
Disjoint 296
Division algebra or ring xix see
Division algebra or ring, centrally finite 30
Division algebra or ring, criterion for 22 42 87 118Ч122
Division algebra or ring, nonassociative 333
Division algebra or ring, noncrossed product finite 164 168 172
Division algorithm 194Ч196
Division ring component 96 99
Divisor see also "HCLF"
Divisor, greatest common 199
Divisor, greatest common left 198
Dot product 7
Duval, P. xii
Edmonds, J.D. xii
Endomorphism 35Ч36 200 208 363 368
Euler, L. 342
EXPONENT 116 119Ч121 122Ч123
Extension, derivations 208Ч211 212
Extension, endomorphisms 36 39Ч40 208Ч211
Extension, iterated 23Ч24
Extension, ring 19
Extension, theorem 96Ч97
Factor set 31 60Ч61 65 71 136 138
Factor set, equivalent 66Ч67 70 74
Factor set, normalized 68
Faith, C. 242
Faithful 77Ч78
Fein, B. and Schacher, M. 58 153 165
Field xix see "Purely
Field extension see also "Field" "Maximal
Field extension, algebraic 60 99 213
Field extension, finite, normal, separable 46 60 72 83 86 103 121 134 161 219
Field extension, maximal separable 100 102
Field extension, nonseparable 89
Field extension, purely inseparable 100
Field extension, separable 89 99 102Ч104 161
Field extension, transcendental 49 55 89 124 164
Field, constants 277
Field, cyclic 45
Field, Differentially Closed 370
Field, formally real 117 124Ч125 143Ч144
Field, perfect 369
Field, real closed 117
Field, subfield: separable, normal, maximal 172
Fields, K. 153
Fields, K. and Herstein, I. 153
Flexible 335 339
Ford, C. 133Ч134 136 149 153
Ford, C. and Janusz, G.J. 149
Formal power series ring see "Power series one "Semigroup
Formally real 117 124 143Ч144
Formanek, E. 155
Free algebra 154 344 351
Free ring 319
Frobenius theorem 2 324Ч326
Frobenius, G. 2 325 326
Fuchs, L. 309 316
Galois group 44 46 64 136 161 322 324 332
Galois group, cyclic 332
Generalized quaternion algebra 20 127
| Generator 243
Generic ring 157
Glassmire, W. 32
Goldie, A.W. 186
Graves, J.T. xi
Greatest comnon divisor = gcd 345Ч346
Group, finite 44
Group, finite multiplicative 135
Group, generalized quaternion 136
Group, rotation 10
Group, semidirect product 134
Group, special orthogonal 10
Hall, M. 136
Hamilton, W.R. xi 1 16
Harris, B. 218
Hasse, H. xii 32 124
HCLF = highest common left factor 346
Herstein, I.N. 84 87 97 116 122 132Ч133 136 214 325 368
Hilbert, D. xiii
Homomorphism 200 208 see
Hopf, H. 333
Idealizer 362
Idempotent 98 110
Inner automorphism 19 84 97Ч98 176 178 229 231 232
Inner product 7 337
Inseparable element 99
Integral domain 345
Involution 5 8 20Ч21 336 338
Irreducible element 198 345
Isbell, J.R. 118 294
Jacobson, N. xvi 18 58 120Ч121 153Ч154 155Ч156 159 162 165 166 171 182 214 269 333
Janusz, G.J. 153
Jategaonkar, A.V. 238 312
Johnson, R.E. 309
Jordan algebra, commutative 335
Jordan algebra, noncommutative 335
Jordan algebra, special 335
Klein, A.A. xv
Kleinfeld, E. 339
Koh, K. xv
Kothe, G. 18 24 89
Kuzmin, E.N. 342
Kyrala, A. xii
L-homomorphism 298Ч299
L-ring 298
Lanczos, C. xii
Lang, S. 47 60 104 150 161 369
Lattice ordered, division ring 318
Lattice ordered, ring 298 304Ч305
Laurent series division ring 161 174
Laurent series field 172Ч174 179
LCRM = least common right multiple 346
Least common multiple = lcm 50 345 348 353 354
Left regular representation 5
Leibniz rule 187Ч188 191 205 209 213Ч214 245Ч251 264 266
Length 61
Length reduction argument 63
Lex, W. xi 333 339Ч340 342
Lie algebra 333 335
Linearly disjoint 173 179 181
Linearly ordered 296
Malcev, A.I. xiv 309
Maximal subfield 75 77Ч78 79Ч82 88Ч91 95 96 162 171 173 175 179 180Ч182
Maximal subfield, nonseparable 89Ч91
Maximal subfield, normal, separable 168Ч169 181
Maximal subfield, separable 89Ч91 95
McCarthy, P.J. 44 56
McHaffey, R. 294
Minimal polynomial 45 49 52 56Ч57 97 133Ч134 170 213 338
Monic 199
Naturally ordered 352
Neumann, B. xiv 294 309 319
Nilpotent derivation 275Ч293
Noether, E. xii 32 124
Noetherian 183 186Ч188 215
Nonassociative division ring 333
Noncrossed product 164Ч165 168Ч169 171Ч172
Noncyclic crossed product 123Ч130
Nonseparable field extension 89
Norm 8 44Ч45
Norm, 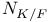 44Ч45 53Ч55 58 44Ч45 53Ч55 58
Norm, nondegenerate 336
Norm, nonsingular 336 337
Normal subfield see "Field extension"
Nucleus 334
o-homomorphism 298Ч299 304
o-isomorphism 298Ч299 304
Octonions 338Ч339
Opposite group 3Ч4 15
Opposite ring 3Ч4 93
Ordered, disjoint 296
Ordered, linearly 296
Ordered, naturally 352
Ordered, positive cone 298
Ore, 0. xiii
Ore, left 197
Ore, right condition 185 316
Ore, right domain 191 215
Ore, right quotient ring 186 191 263 267
Osborn, J.M. 342
Partially ordered ring 298
Partially ordered semigroup 297
Perfect field 369
Po-ring 298
Po-semigroup 297
Po-set = Partially ordered set 296
Polynomial identity 155 159
Polynomial ring, left skew 197
Polynomial ring, skew 183Ч184 189 192Ч193 199 263 302 357 361
Polynomial ring, twisted 227 237 344 345 369Ч370
Polynomial ring, twisted skew 366
Positive cone 298
Power associative 334
Power series, one variable see also "Semigroup power series"
Power series, one variable, division ring 200Ч202
Power series, one variable, Laurent 202 205 206 211
Power series, one variable, ring 200 204Ч205 207 210 352
Prime algebra, ring 158Ч160
Prime element, invariant 347
Prime element, left 347
Primitive root of unity 133 137 150 161 264 285 361Ч362
Principal right ideal 187
Principal right ideal, domain = PRID 188 215Ч216 313Ч315 344 346 350Ч352
Principal right ideal, ring 187
Procesi, C. 153Ч154 155
Pseudo linear extension 242
Purely inseparable 100
pЧAlgebra 124
Quadratic algebra 335
Quadratic algebra, nonassociative 337
Quadratic form 11
Quadratic ring extension 40 288 322
Quartic extension 18
Quartic field 125 237 327Ч332
Quaternionic extension 20
Quaternions 1 49Ч51
Quaternions, generalized 20
Quaternions, real 6 49Ч51
Rational function field 89Ч90 118
Real closed 117
Relatively prime 53 345
Representation 4 21 25Ч26 89Ч90 135
Representation, right regular 5
Rinehart, G. 215
Root, left 362
Root, noncommutative polynomial 360
Root, right 362
Rotation group 10Ч17
Scalar product 7
Schacher, M. xiii 153
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте