|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Thompson W.J. — Computing for Scientists and Engineers: A Workbook of Analysis, Numerics, and Applications |
|
|
 |
| Предметный указатель |
Fourier series, generalized sawtooth 350-353
Fourier series, generalized sawtooth properties 352
Fourier series, in complex-exponential form 335
Fourier series, in cosine and sine form 335
Fourier series, interpreting coefficients 336
Fourier series, overview 317
Fourier series, program for 340-343
Fourier series, sawtooth function 347-349
Fourier series, sawtooth related to square pulse 347
Fourier series, square-pulse function 338-340
Fourier series, wedge function 343-345
Fourier series, wedge related to square pulse 345
Fourier series, window function 345-347
Fourier series, window related to square pulse 346
Fourier transform of 325
Free motion, critical damping 263
Free motion, damping parameter for 262
Free motion, natural frequency for 262
Free motion, second-order differential equations for 261
Full Width at Half Maximum (FWHM) 183
Function in C language,  310 310
Function in C language,  310 310
Function in C language,  251 290 297 251 290 297
Function in C language,  for Schr for Schr dinger equation 301 dinger equation 301
Function in C language,  363 363
Function in C language,  22 22
Function in C language,  26 26
Function in C language,  22 22
Function in C language,  26 26
Function in C language,  22 22
Function in C language,  400 400
Function in C language,  68 68
Function in C language,  22 22
Function in C language,  109 109
Function in C language,  109 109
Function in C language,  110 110
Function in C language,  110 110
Function in C language,  109 109
Function in C language,  233 233
Function in C language,  415 415
Function in C language,  362 362
Function in C language,  342 342
Function in C language,  341 341
Function in C language,  341 341
Function in C language,  342 342
Function in C language,  251 290 296 251 290 296
Function in C language,  for Schr for Schr dinger eguation 301 dinger eguation 301
Function in C language,  310 310
Function in C language,  310 310
Function in C language,  120 120
Function in C language,  109 109
Function in C language,  416 416
Function in C language,  166 166
Function in C language,  105 105
Function in C language,  417 417
Function in C language,  416 416
Function in C language,  416 416
Function in C language,  216 216
Function in C language,  48 48
Function in C language,  48 48
Function in C language,  206 206
Function in C language,  95 95
Function in C language,  96 96
Function in C language,  94 94
Function in C language,  94 94
Function in C language,  96 96
Function in C language,  95 95
Function in C language,  138 149 138 149
Function in C language,  69 69
Function in C language,  163 163
Function in C language,  165 165
Function in C language,  165 165
Function in C language, 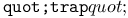 417 417
Function in C language,  138 149 138 149
Function in C language,  150 150
Function in C language,  139 150 139 150
Function in C language,  166 166
Function in C language,  for spline 166 for spline 166
Function in C language,  for trapezoid and Simpson 139 for trapezoid and Simpson 139
Functions, index of 429-430
Fundamental frequency in Fourier series 336
Fusion-energy devices and Voigt profile 419
FWHM, additivity for Lorentzian convolutions 404
FWHM, of Gaussian distribution 183
FWHM, of Lorentzian function 389
Galilei, Galileo 273 279 313
Gauss plane see Complex plane
Gauss, C. F. 182
Gaussian distribution 182-183 210 386
Gaussian distribution, and Heisenberg Uncertainty Relations 388
Gaussian distribution, and maximum likelihood 182
Gaussian distribution, as Dirac delta distribution 389
Gaussian distribution, compared with Lorentzian function 390
Gaussian distribution, convolution of 402
Gaussian distribution, convolution with Lorentzian 406-411
Gaussian distribution, FFT of discretized 387
Gaussian distribution, Fourier integral transform of 386-389
Gaussian distribution, fourth moment of 212
Gaussian elimination in spline fits 158
Gaussian quadrature 144
Gear, C. W. 312 313
Gehani, N. 8 15 423
Generalized logistic equation 239
Generalized logistic growth 239-241
Generalized logistic growth, curves of 240
Generalized sawtooth, Fourier series for 350-353
Geometric series 52-56
Geometric series, definition and properties 52
Geometric series, for deriving DFT 3 19
Geometric series, for DFT of general exponential 323
Geometric series, integral to derive logarithm series 57
Geometric series, program for 53
Gibbs phenomenon see Wilbraham — Gibbs overshoot
Gibbs, J. W. 349 376
Gilbert, D. 277 313
Gleick. J. 239 255
Gould, H. 3 14
Graphics 11-12
Graphics, and Mathematica 12
Great Fire of London and rebuilding St. Paul's 279
Haberman, R. 239 255 264 313
Hamming, R. W. 375 376 397 420
Harbison, S. P. 8 15
Harmonic analyzer 349
Harmonic expansion see Fourier series harmonic oscillation discrete
Harmonic oscillation, Fourier integral transform 382
Harmonics in Fourier series 336
Hartley transform 334
Harvesting effects on logistic growth 238
Hasse, R. W. 236 255
Heisenberg uncertainty relations 388
Hermite polynomials 300
Hofstadter, D. R. 85 98
Homer polynomial, algorithm for 103
Homer polynomial, for cosine and sine 67
Homer polynomial, for spline integration 176
Homer polynomial, of limited use for series 105
Homer polynomial, program for 104
Homogeneous differential equation 224
Honig, E. 278 279 313
Hooke's law 259
Hooke, Robert 279
Hosmer, D. W. 241 255
Huygens, Christian 279
Hyperbolic functions 34-37
Hyperbolic functions, Cosh 34
Hyperbolic functions, graphs of 371
Hyperbolic functions, sign rule and circular functions 35
Hyperbolic functions, Sinh 34
Hyperbolic functions, Tanh 36
| Hyperbolic functions, Taylor series for 71
Imaginary number 18 19
Independent diagonal weighting model (IDWM) 192 193 196 197
Independent diagonal weighting model (IDWM), with constant weights (IDWMC) 192
Induction, and recurrence 84
Induction, for convolution of Gaussians 403
Induction, for convolution of Lorentzians 405
Induction, for convolution of Voigt profiles 408
Induction, geometric series by 52
Induction, Taylor's theorem proof by 59
infinite loop see Loop infinite
Ingard, K. U. 43 49 269 313 386 420
Initial conditions of differential equations 223
Integrals, analytical, by Mathematica 99
Integrals, numerical 133-144
Integrals, numerical, comparison of trapezoid and Simpson rules 142
Integrals, numerical, for potential from a charged wire 145
Integrals, numerical, higher-order methods 144
Integrals, numerical, Simpson formula 140
Integrals, numerical, testing with cosines 143
Integrals, numerical, trapezoid formula 135
Integrals, numerical, with constant stepsize 134-135
Integration by splines see Spline integration
Interpolation by splines see Spline interpolation
Inverse circular functions, Taylor series for 70
Isobe 199 218
Iteration 84
Jaffe, A. J. 181 218
Jain, M. K. 247 255 304 312 313
K rner, T. W. 318 350 376 rner, T. W. 318 350 376
Keller model of world-record sprints 226
Keller, J. B. 226 255
Kellison, S. G. 83 98
Kemighan, B. W. 11 15 85 98
Kerrigan, J. F. 8 15 423
Kinematics of sprinting see World-record sprints
Kinsella, A. 218
Kirchhoffs second law 260
Knot see Spline
Koenig, A. 8 15
Koonin, S. E. 3 14
Kronecker delta and Dirac delta distributions 380
L'H pital's rule, used for DFT of exponential decay 323 pital's rule, used for DFT of exponential decay 323
L'H pital's rule, used for DFT of harmonic oscillation 325 pital's rule, used for DFT of harmonic oscillation 325
Lancaster, P. 178 179
Lanczos filter 373-375
Landau, R. H. 421 422
Language, and Fortran 7
Language, and Mathematica 10
Language, and Numerical Recipes 10
Language, and Pascal 6
Language, exit function 9
Language, for Fortran programmers 8
Language, for Pascal programmers 8
Language, learning to program in 7 16
Language, portability of 7
Language, simple program (geometric series) 55
Language, translating between Fortran and C 423-428
Language, translating between Pascal and C 423-428
Language, translating to Fortran from 8
Language, translating to Pascal from 8
Language, workstations and C 7
Least squares, least-squares fitting, and maximum likelihood 182
Least squares, linear least squares, and discrete Fourier transforms 3 19
Least-squares criterion 182-185
Least-squares fitting see also Linear
Least-squares fitting, combined with splines 218
Least-squares fitting, compared to splines 181
Least-squares fitting, disadvantages of 184
Least-squares fitting, outlier influence 184
Least-squares fitting, weights in 185
Least-squares normalization factors see Normalization factors by least squares
Legendre and least-squares criterion 182
Legendre polynomials 187
Lewis, Carl 233
Lichten, W. 181 218
Lichtenberg, D. B. 235 255
Lindstrom, P. A. 83 98
Linear least squares see also Straight-line
Linear least squares, and orthogonal functions 185 188
Linear least squares, equations for coefficients 188
Links between chapters 13
Logarithm functions, programming series for 90
Logarithm functions, Taylor series for 72-75
Logarithmic transformation and parameter bias 214
Logarithmic transformation, of Lorentzian function 393
Logarithmic transformation, parameter bias in 208
Logistic distribution, logistic growth 235-241
Logistic distribution, logistic growth, and ecology 235
Logistic distribution, logistic growth, curve of 236
Logistic distribution, logistic growth, differential equation for 235
Logistic distribution, logistic growth, dimensionless form 237
Logistic distribution, logistic growth, equilibrium condition 236
Logistic distribution, logistic growth, generalized 239-241
Logistic distribution, logistic growth, graphs of 237
Logistic distribution, logistic growth, harvesting effects 238
Logistic distribution, logistic growth, origins of 235
Logistic distribution, logistic growth, point of inflexion 238
Logistic distribution, logistic growth, predicting extinction 239
Logistic distribution, logistic growth, properties of 238-239
Logistic distribution, logistic growth, stability and chaos 239
Logistic distribution, logistic growth, various terms for 236
loop, infinite see Infinite loop
Lorentzian function for resonance 268
Lorentzian functions 389-393
Lorentzian functions, binning effects on 396
Lorentzian functions, compared with Gaussian distribution 390
Lorentzian functions, convolution of 403
Lorentzian functions, convolution with Gaussian 406411
Lorentzian functions, convolution with window function 394
Lorentzian functions, definition of 389
Lorentzian functions, Fourier integral transform of 391-393
Lorentzian functions, FWHM of 389
Lorentzian functions, normalized 405
Lorentzian functions, resonance frequency 389
Lorentzian trajectory in complex plane 39
Lumped-parameter analysis of world-record sprints 226
Lyons, L. 181 219
M ldner 8 15 423 ldner 8 15 423
Macdonald, J. R. 190 191 219
Maclaurin series see Taylor series
Madelung transformation for stiff differential equations 311
Mandala for FFT algorithm 330
Maron, M. J. 117 144 151
Mathematica 5 20 49 52 421
Mathematica, for ordinary differential equations 224
Mathematical modeling 2
Maximum likelihood and least-squares fitting 182 185
Mechanical-electrical analogs 259-261
Menai Strait 277
Meredith, D. C. 3 14
Mesterton — Gibbons 2 14
Meyer, W. J. 2 14
Michelson, Albert 349
Mihalas, D. 404 419 420
Miller, W. 69 98
Modi, J. J. 5 14
Modulus, program for 25
Moment of inertia and least-squares straight line 190
Monte Carlo simulation, for error estimating 218
Monte Carlo simulation, for parameter bias 214
Nakamura, S. 3 14 144 151 304 313
Natural frequency for free motion 262
Natural spline see also Spline
Natural spline, compared to exact endpoint conditions 161
Natural spline, endpoint conditions 160-161
Natural spline, minimal curvature property of 160
Negative feedback and logistic growth 235
Newton's equation as pair of first-order equations 258
Newton, Isaac, and uniform-density catenary 279
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте






 dinger equation
dinger equation 














































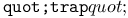




 for spline
for spline  for trapezoid and Simpson
for trapezoid and Simpson  pital's rule, used for DFT of exponential decay
pital's rule, used for DFT of exponential decay  ldner
ldner