|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Penrose R., Rindler W. — Spinors and space-time. Spinor and twistor methods in space-time geometry |
|
|
 |
| Предметный указатель |
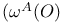 , , 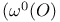 (values at origin) 48 (values at origin) 48
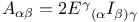 (angular momentum twistor) 71 (angular momentum twistor) 71
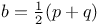 (boost-weight) 29 (boost-weight) 29
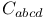 (Weyl tensor) 20 (Weyl tensor) 20
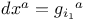 437 437
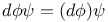 , , 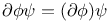 etc. 16 etc. 16
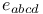 (alternating tensor) 10 11 (alternating tensor) 10 11
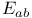 (source for linear gravity) 38 (source for linear gravity) 38
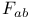 , , 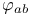 , , 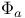 , , 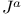 , , 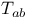 (Maxwell theory) 32 (Maxwell theory) 32
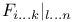 (restriction) 159 (restriction) 159
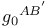 etc. (translation symbols) 8 etc. (translation symbols) 8
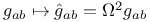 35 35
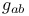 (metric tensor) 5 (metric tensor) 5
![$I^{+}[\Sigma], I^{-}[\Sigma]$](/math_tex/da7821c751304c6d1e298c8a0e8d22dd82.gif) (future-, past-set) 296 (future-, past-set) 296
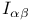 , , 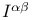 (infinity twistors) 66 (infinity twistors) 66
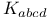 (linearized curvature) 38 (linearized curvature) 38
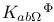 , , 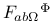 , , 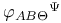 , , 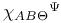 (bundle curvature) 34 35 (bundle curvature) 34 35
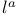 , , 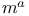 , , 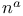 (null tetrad) 6 (null tetrad) 6
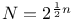 or or 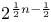 (spin-space dimension) 440 (spin-space dimension) 440
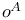 , , 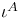 (spinor basis) 6 (spinor basis) 6
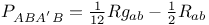 122 122
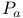 , , 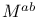 (momentum, angular momentum) 68 (momentum, angular momentum) 68
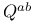 (spin-lowering tensor) 77 (spin-lowering tensor) 77
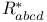 , , 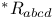 , , 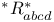 19 19
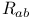 , R 20 , R 20
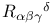 (curvature tensor) 15 19 (curvature tensor) 15 19
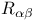 (dual of (dual of 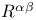 ) 65 ) 65
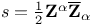 (helicity) 56 (helicity) 56
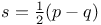 (spin-weight) 29 (spin-weight) 29
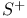 (anti-celestial sphere) 1 380 (anti-celestial sphere) 1 380
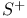 (anti-celestial sphere) and general symmetric spinor 265 (anti-celestial sphere) and general symmetric spinor 265
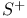 (anti-celestial sphere) and Weyl spinor 226 249 (anti-celestial sphere) and Weyl spinor 226 249
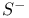 (celestial sphere) 2 (celestial sphere) 2
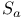 (Pauli — Lubanski) 69 (Pauli — Lubanski) 69
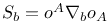 174 174
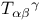 (torsion tensor) 15 (torsion tensor) 15
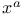 (Minkowski coordinates) 1 46 (Minkowski coordinates) 1 46
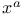 (position vector) 45 (position vector) 45
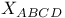 , , 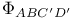 , ,  (curvature spinors) 19 (curvature spinors) 19
![$[^{1}_{0}]$](/math_tex/7e5cb3ef29d19dc61866eea946da117282.gif) , , ![$[^{0}_{1}],..., [^{p}_{q}]$](/math_tex/63301f00ec8eccc96d4d27286b9d125682.gif) (twistor valence) 46 48 51 (twistor valence) 46 48 51
![$[^{r}_{p} {}^{s}_{q}]$](/math_tex/eee456d033271740c93de2ddee32aac482.gif) (spinor valence symbol) 10 (spinor valence symbol) 10
 -plane description of twistors 64 -plane description of twistors 64
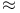 (weak equality) 354 (weak equality) 354
 (Sparling 3-form) 434 (Sparling 3-form) 434
 -plane description of dual twistors 64 -plane description of dual twistors 64
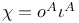 6 6
![$\chi...(...)...,\chi...[...]...,\chi...|...|...$](/math_tex/eefaec1d0d3c525b6690893c954d7bef82.gif) 9 9
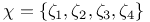 (cross-ratio) 2 (cross-ratio) 2
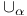 , , 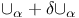 (neighbouring null twistors) 181 (neighbouring null twistors) 181
 (coboundary operator) 161 (coboundary operator) 161
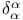 , , 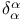 (basis vectors) 4 (basis vectors) 4
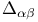 (derivative commutator) 15 (derivative commutator) 15
 (correction factor) 402 (correction factor) 402
 (ray) 358 (ray) 358
![$\gamma_{ab...d} = \gamma_{[a}\gamma_{b}...\gamma_{d]}$](/math_tex/f65b043eb1dd4a1b62eb28394f046bdc82.gif) , , 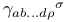 444 445 444 445
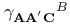 (spin-coefficients) 18 (spin-coefficients) 18
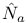 (normal to (normal to 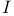 ) 352 ) 352
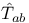 (trace-reversed (trace-reversed 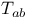 ) 11 ) 11
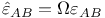 35 35
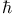 (Planck's constant/ (Planck's constant/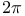 ) 142 ) 142
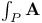 (integral of p-form) 17 (integral of p-form) 17
 (spin-vector) 2 3 (spin-vector) 2 3
 (cosmological constant) 20 (cosmological constant) 20
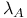 (Witten spinor) 430 (Witten spinor) 430
 (= complexified) 64 (= complexified) 64
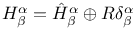 (Hermitian twistors) 95 (Hermitian twistors) 95
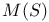 , , 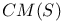 (associated Minkowski spaces) 418 (associated Minkowski spaces) 418
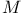 (Minkowski space) 1 (Minkowski space) 1
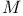 (compactified (compactified 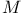 ) 298 ) 298
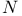 , , 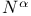 , , 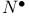 , , 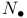 (space of rays in (space of rays in 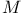 ) 207 ) 207
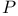 (= projective) 56 57 (= projective) 56 57
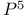 300 300
 (real locus) 266 (real locus) 266
![$\mathbb{R}^{[\alpha,\beta]}$](/math_tex/d1bc7a88c97a2bbb63a4fac378c7e00e82.gif) (twistor-real) 95 (twistor-real) 95
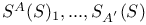 (asymptotic twistor spin-spaces) 417 (asymptotic twistor spin-spaces) 417
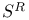 , , 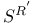 (reduced spin-spaces) 443 (reduced spin-spaces) 443
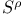 (spin-space for n dimensions) 441 (spin-space for n dimensions) 441
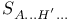 (constant spinors) 30 (constant spinors) 30
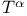 ( (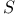 ) (2-surface twistor space) 399 ) (2-surface twistor space) 399
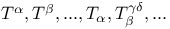 (twistor spaces) 46 47 (twistor spaces) 46 47
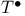 , , 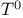 = = 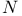 , , 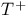 , , 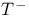 , , 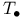 etc. 56 (57) etc. 56 (57)
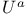 , , 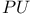 (hyperplane) 456 (hyperplane) 456
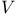 (Minkowski vector space) 1 (Minkowski vector space) 1
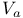 (n-dimensional vector space) 441 (n-dimensional vector space) 441
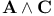 (exterior product) 16 (exterior product) 16
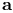 , , 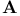 , , 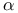 , , 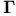 (bold upright indices: numerical) 4 (bold upright indices: numerical) 4
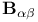 , , 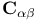 , , 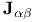 (bang, crunch etc.) 343 344 (bang, crunch etc.) 343 344
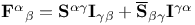 (Killing vector twistor) 87 (Killing vector twistor) 87
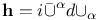 , , 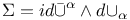 209 209
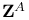 , , 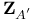 (spinor parts) 47 (spinor parts) 47
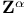 , , ![$[\omega^{A}]$](/math_tex/570c895cf98a1481c0d980f3bae2a70882.gif) , , 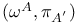 (twistor) 46 47 (twistor) 46 47
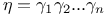 442 442
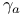 , , 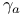 , , 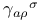 , , 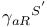 ( ( -matrices) 441 443 -matrices) 441 443
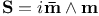 (surface-area 2-form) 27 (surface-area 2-form) 27
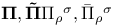 (projections to reduced spaces) 443 (projections to reduced spaces) 443
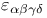 (alternating twistor) 54 (alternating twistor) 54
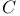 (Clifford algebra) 442 (Clifford algebra) 442
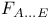 , , 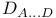 (spinor sheaves) 117 (spinor sheaves) 117
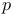 (th), (th), 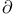 (eth), (eth), 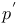 , , 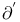 23 23
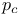 , , 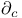 , , 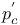 , , 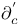 (conformally invariant: notation change from volume 1!) 36 (conformally invariant: notation change from volume 1!) 36
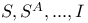 4 4
![$\mathfrak{\sigma^{\mathscr{A}}}[P]$](/math_tex/c35882b63f27cd3b10259873d9c3c78182.gif) , , ![$\mathfrak{\sigma^{\mathscr{A}}}[\mathscr{U}]$](/math_tex/c4d1e37b68cb51325a3a0b8c02e3b97e82.gif) 5 5
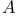 (anti-Einstein) 333 (anti-Einstein) 333
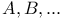 (clumped indices) 4 (clumped indices) 4
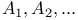 (similarly clumped indices) 5 (similarly clumped indices) 5
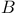 (BMS group) 381 (BMS group) 381
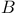 (spin-vector bundle) 437 (spin-vector bundle) 437
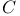 (complex conjugation) 313 459 (complex conjugation) 313 459
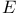 (Einstein cylinder) 294 (Einstein cylinder) 294
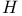 (hypersurface) 215 (hypersurface) 215
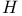 -space (Newman's 'Heaven') 129 389 -space (Newman's 'Heaven') 129 389
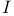 ('scri'), ('scri'), 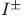 , , 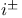 , , 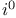 291 291
 (null cone in (null cone in 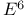 ) 301 ) 301
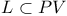 (quadric in projective space) 452 (quadric in projective space) 452
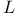 (labelling set) 4 (labelling set) 4
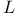 (Lorentz group) 383 (Lorentz group) 383
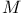 (manifold, space-time) 3 (manifold, space-time) 3
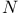 (null volume 3-form) 28 (null volume 3-form) 28
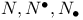 (space of rays in (space of rays in 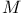 ) 208 ) 208
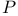 (Poincare group) 384 (Poincare group) 384
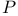 , , 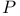 (Minkowski 3-space) 187 188 (Minkowski 3-space) 187 188
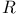 (Lorentz rotations) 382 (Lorentz rotations) 382
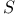 (spacelike 2-surface) 26 398 (spacelike 2-surface) 26 398
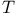 (translations) 381 (translations) 381
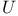 (super translations) 381 (super translations) 381
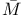 (manifold-with-boundary) 291 (manifold-with-boundary) 291
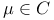 (ray of null congruence) 169 (ray of null congruence) 169
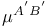 (angular momentum spinor) 71 (angular momentum spinor) 71
 (covariant derivative) 15 (covariant derivative) 15
 (function on (function on 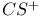 ), ),  266 266
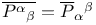 56 56
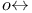 (origin-dependent correspondence) 47 (origin-dependent correspondence) 47
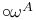 , , 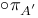 (constant spinors) 46 (constant spinors) 46
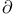 (boundary) 17 (boundary) 17
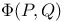 (squared interval) 1 (squared interval) 1
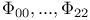 (Ricci spinor components) 22 (Ricci spinor components) 22
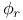 (components of massless field) 26 (components of massless field) 26
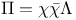 22 22
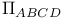 (Plebanski spinor) 265 (Plebanski spinor) 265
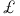 (Lie derivative) 16 (Lie derivative) 16
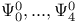 (Weyl components at (Weyl components at 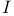 ) 364 ) 364
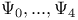 (Weyl spinor components) 22 (Weyl spinor components) 22
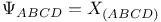 (Weyl spinor) 20 (Weyl spinor) 20
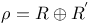 (spinor abstract indices reduced) 443 (spinor abstract indices reduced) 443
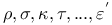 (spin coefficients) 18 (spin coefficients) 18
 (symplectic invariant) 184 (symplectic invariant) 184
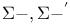 generator (on generator (on 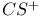 ) 267 ) 267
![$\sigma...(...)...,\sigma...[...]...$](/math_tex/f4b9e2800800dac11e7e8955a1aba45d82.gif) 9 9
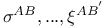 ,... (primary parts) 55 ,... (primary parts) 55
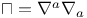 (D'Alembertian) 39 (D'Alembertian) 39
| 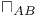 , , 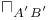 (spinor commutator) 21 (spinor commutator) 21
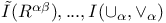 (infinity functions) 341 (infinity functions) 341
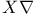 (directional derivative) 17 (directional derivative) 17
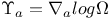 35 35
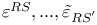 449 449
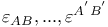 5 5
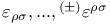 , , 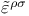 447 448 447 448
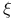 (holomorphic coordinate for (holomorphic coordinate for 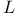 ) 27 ) 27
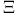 (Witten 2-form) 430 (Witten 2-form) 430
 (complex stereographic coordinate) 1 31 (complex stereographic coordinate) 1 31
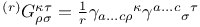 454 454
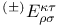 , , 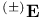 445 445
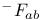 , , 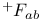 12 12
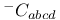 , , 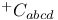 , , 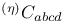 21 21
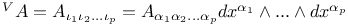 (p-form) 16 17 (p-form) 16 17
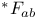 , , 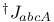 , , 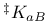 (duals) 11 (duals) 11
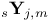 (basis for harmonics) 31 (basis for harmonics) 31
'Copies' of spin-space in odd dimension (440) 458 459
(...)' 19
(p, q)-curve 267
A (scaling at 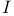 ) 355 371 ) 355 371
a = AA', b = BB', etc. 5
a, A,  , ,  (lightface sloping indices: abstract) 4 (lightface sloping indices: abstract) 4
Abreastness in twistor terms 181 182
Abreastness of non-abreast rays 185
Abreastness of rays 173 176 183 207 215 216
Abstract-index formalism 3
Abstract-index formalism for TV-dimensional spinors 441
Achronal hypersurface 431
Adams, J.F. 441 461
Addition of twistors 47
ADM (Arnowitt — Deser — Misner) mass 404 433
Advanced time coordinate 292 348 356
Affine parameter 170 292
Affine parameter in compacted formalism (182)
Affine parameter under conformal rescaling 360
Affine parametrization of ray (null geodesic) 170 172
Aitken, A.C. (285)
Algebraically special 190 191 205 206
Almost complex manifold 213 214
Alpha-curve 218 390
Alpha-plane (surface) 64 164 309
Alpha-plane (surface), higher-dimensional 453 457 458 460 461
Alternating tensor 10 11
Alternating tensor, n-dimensional 442
Alternating twistor 54 65 (328)
Alternating twistor for 2-surface twistors 408 418 419
Alternative law 462
Ambitwistor (164) 462
Analyticity (real-analytic) 128 (191) 201 215 (351) see
Angular momentum (moment, kinematic) twistor 71 73 85 401
Angular momentum at 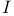 420 420
Angular momentum for asymptotically flat space 44 392 420
Angular momentum for linear gravity 75 395
Angular momentum in general relativity 395
Angular momentum of Kerr solution 109 204 205
Angular momentum of Kerr space-time 109 205
Angular momentum, (anti)-self-dual 419
Angular momentum, Quantized 144
Angular momentum, tensor 68
Angular momentum, total 110
Angular momentum, twistor 71 85 92
Angular momentum, twistor and Kerr's theorem 203 204
Angular momentum, twistor, apparent paradox 77 88 93
Angular momentum, twistor, quantized 144 148
Angular momentum, twistor, quasi-local version 402
Angular momentum, twistor, twistor version (149)
Anti-celestial sphere 1
Anti-de Sitter space 336
Anti-Einstein universe 333
Anti-Grgin behaviour of massless free field 330
Anti-self-dual 12 242 452
Anti-self-dual, Weyl curvature 21 129 164 390
Anti-self-dual, Yang — Mills curvature 35 164
Anti-symmetric (skew) tensor 11 12 14 see form"
Anti-symmetric (skew) tensor, simple 14 247 451 452
Arnol'd, V.I. 211
Arnowitt — Deser — Misner (ADM) mass 404 429 433
Arnowitt, R. 404 429
Aronson, B. 389
Ashtekar — Hansen angular momentum 404
Ashtekar, A. (353) 404 429
Astigmatism of curvature 230 (231)
Asymptotic Einstein condition 352 354 363
Asymptotic Einstein condition eliminates logarithms 362
Asymptotic Einstein condition, strong 357 367 409
Asymptotic flatness 350 see conformal"
Asymptotic simplicity 292 347 351 see conformal"
Asymptotic simplicity, future 353 367 408
Asymptotic simplicity, weak 351 353
Asymptotic spin space 411 417
Asymptotic symmetry group 366
Asymptotic symmetry group for FRW (Friedmann — Robertson — Walker) models 366
Asymptotic twistors 212 389 390
Asymptotically plane wave front 377 378
Atiyah — Singer index (theorem) 399 454
Atiyah, M.F. 44 (129) 390 434 464
Bach tensor 127 (133) 137
Bach, R. 127
Backward tube 316
Bad cut 384
Bailey, T.N. (149) 152
Bang twistor 342
Bardeen, J.M. 350 428
Basis 4
Basis 1-forms in abstract-index formalism 17 437 438
Basis for twistors 48
Basis, 2-spinor basis 6
Basis, n-dimensional (spinor) basis 442
Basis, twistor basis 48
Basis, twistor basis, dual 50
Bateman, H. (139)
Bel — Robinson tensor (85)
Bel, L. (85)
Bergmann, P.G. 77
Beta-curve 217 219 390 406
Beta-plane 64 217 309
Beta-plane, higher-dimensional 453 457 458 460 461
Bianchi identity 22 121 196 356
Bianchi identity in compacted spin-coefficient (GHP) 25 26
Bianchi identity in terms of 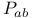 123 387 123 387
Bianchi identity, linearized 38
Bianchi identity, spin-coefficient form (compacted) 25 26 424
Bianchi identity, spinor form 22 424
Bianchi identity, spinor form of Yang — Mills theory 35
Bianchi identity, spinor form, Einstein — Maxwell case 34
big bang 335 343 345
Big crunch 335 336 343
Bivectors 11 242
Bivectors, simple 14
Black and white regions on 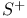 (anti-celestial sphere) 275 (anti-celestial sphere) 275
Black hole 204 351
BMS (Bondi — Metzner — Sachs) group 366 369
BMS (Bondi — Metzner — Sachs) group and (super-) translations 381
BMS (Bondi — Metzner — Sachs) group and Lorentz rotations 382
BMS (Bondi — Metzner — Sachs) group for 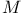 380 381 380 381
Bocher, M. 298
Bondi (retarded) time coordinate 373 380 393
Bondi parameter 367 368
Bondi parameter for infinity (conformal) 367 373
Bondi system 386
Bondi time coordinate for infinity (conformal) 373 380 393
Bondi — Metzner — Sachs group 369 370 see
Bondi — Sachs mass, momentum 44 392 396 (406) 415 423 431 see
Bondi — Sachs mass, momentum from Hawking expression 416
Bondi — Sachs mass, momentum, mass loss theorem 424
Bondi — Sachs mass, momentum, positivity 429
Bondi — Sachs metrics 350
Bondi — Sachs news function 386 425
Bondi, H. 179 185 336 350 (396) 415 (424)
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



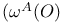 ,
, 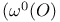 (values at origin)
(values at origin) 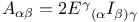 (angular momentum twistor)
(angular momentum twistor) 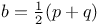 (boost-weight)
(boost-weight) 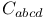 (Weyl tensor)
(Weyl tensor) 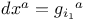
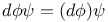 ,
, 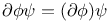 etc.
etc. 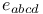 (alternating tensor)
(alternating tensor) 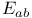 (source for linear gravity)
(source for linear gravity) 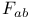 ,
, 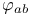 ,
, 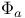 ,
, 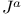 ,
, 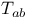 (Maxwell theory)
(Maxwell theory) 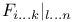 (restriction)
(restriction) 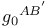 etc. (translation symbols)
etc. (translation symbols) 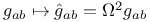
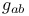 (metric tensor)
(metric tensor) ![$I^{+}[\Sigma], I^{-}[\Sigma]$](/math_tex/da7821c751304c6d1e298c8a0e8d22dd82.gif) (future-, past-set)
(future-, past-set) 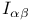 ,
, 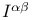 (infinity twistors)
(infinity twistors) 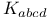 (linearized curvature)
(linearized curvature) 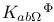 ,
, 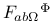 ,
, 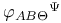 ,
, 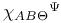 (bundle curvature)
(bundle curvature) 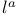 ,
, 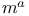 ,
, 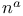 (null tetrad)
(null tetrad) 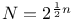 or
or 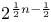 (spin-space dimension)
(spin-space dimension) 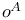 ,
, 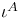 (spinor basis)
(spinor basis) 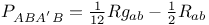
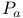 ,
, 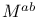 (momentum, angular momentum)
(momentum, angular momentum) 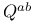 (spin-lowering tensor)
(spin-lowering tensor) 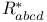 ,
, 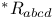 ,
, 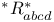
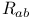 , R
, R 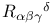 (curvature tensor)
(curvature tensor) 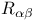 (dual of
(dual of 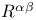 )
) 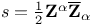 (helicity)
(helicity) 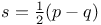 (spin-weight)
(spin-weight) 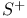 (anti-celestial sphere)
(anti-celestial sphere) 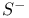 (celestial sphere)
(celestial sphere) 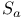 (Pauli — Lubanski)
(Pauli — Lubanski) 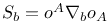
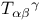 (torsion tensor)
(torsion tensor) 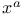 (Minkowski coordinates)
(Minkowski coordinates) 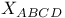 ,
, 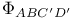 ,
,  (curvature spinors)
(curvature spinors) ![$[^{1}_{0}]$](/math_tex/7e5cb3ef29d19dc61866eea946da117282.gif) ,
, ![$[^{0}_{1}],..., [^{p}_{q}]$](/math_tex/63301f00ec8eccc96d4d27286b9d125682.gif) (twistor valence)
(twistor valence) ![$[^{r}_{p} {}^{s}_{q}]$](/math_tex/eee456d033271740c93de2ddee32aac482.gif) (spinor valence symbol)
(spinor valence symbol)  -plane description of twistors
-plane description of twistors 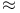 (weak equality)
(weak equality)  (Sparling 3-form)
(Sparling 3-form) 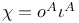
![$\chi...(...)...,\chi...[...]...,\chi...|...|...$](/math_tex/eefaec1d0d3c525b6690893c954d7bef82.gif)
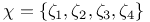 (cross-ratio)
(cross-ratio) 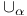 ,
, 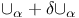 (neighbouring null twistors)
(neighbouring null twistors)  (coboundary operator)
(coboundary operator) 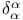 ,
, 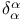 (basis vectors)
(basis vectors) 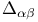 (derivative commutator)
(derivative commutator)  (correction factor)
(correction factor)  (ray)
(ray) ![$\gamma_{ab...d} = \gamma_{[a}\gamma_{b}...\gamma_{d]}$](/math_tex/f65b043eb1dd4a1b62eb28394f046bdc82.gif) ,
, 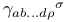
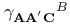 (spin-coefficients)
(spin-coefficients) 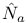 (normal to
(normal to 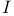 )
) 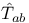 (trace-reversed
(trace-reversed 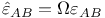
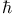 (Planck's constant/
(Planck's constant/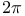 )
) 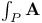 (integral of p-form)
(integral of p-form)  (spin-vector)
(spin-vector)  (cosmological constant)
(cosmological constant) 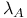 (Witten spinor)
(Witten spinor)  (= complexified)
(= complexified) 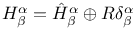 (Hermitian twistors)
(Hermitian twistors) 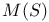 ,
, 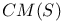 (associated Minkowski spaces)
(associated Minkowski spaces) 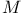 (Minkowski space)
(Minkowski space) 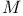 (compactified
(compactified 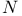 ,
, 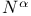 ,
, 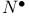 ,
, 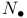 (space of rays in
(space of rays in 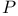 (= projective)
(= projective) 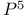
 (real locus)
(real locus) ![$\mathbb{R}^{[\alpha,\beta]}$](/math_tex/d1bc7a88c97a2bbb63a4fac378c7e00e82.gif) (twistor-real)
(twistor-real) 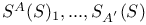 (asymptotic twistor spin-spaces)
(asymptotic twistor spin-spaces) 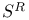 ,
, 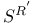 (reduced spin-spaces)
(reduced spin-spaces) 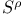 (spin-space for n dimensions)
(spin-space for n dimensions) 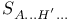 (constant spinors)
(constant spinors) 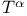 (
(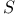 ) (2-surface twistor space)
) (2-surface twistor space) 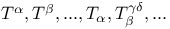 (twistor spaces)
(twistor spaces) 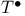 ,
, 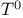 =
= 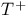 ,
, 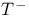 ,
, 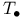 etc.
etc. 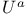 ,
, 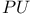 (hyperplane)
(hyperplane) 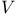 (Minkowski vector space)
(Minkowski vector space) 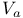 (n-dimensional vector space)
(n-dimensional vector space) 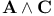 (exterior product)
(exterior product) 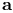 ,
, 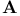 ,
, 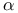 ,
, 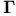 (bold upright indices: numerical)
(bold upright indices: numerical) 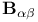 ,
, 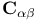 ,
, 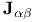 (bang, crunch etc.)
(bang, crunch etc.) 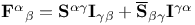 (Killing vector twistor)
(Killing vector twistor) 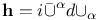 ,
, 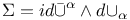
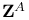 ,
, 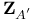 (spinor parts)
(spinor parts) 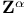 ,
, ![$[\omega^{A}]$](/math_tex/570c895cf98a1481c0d980f3bae2a70882.gif) ,
, 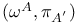 (twistor)
(twistor) 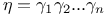
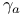 ,
, 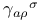 ,
, 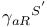 (
(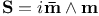 (surface-area 2-form)
(surface-area 2-form) 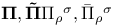 (projections to reduced spaces)
(projections to reduced spaces) 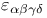 (alternating twistor)
(alternating twistor) 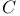 (Clifford algebra)
(Clifford algebra) 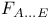 ,
, 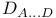 (spinor sheaves)
(spinor sheaves) 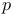 (th),
(th), 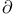 (eth),
(eth), 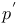 ,
, 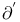
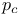 ,
, 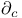 ,
, 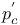 ,
, 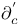 (conformally invariant: notation change from volume 1!)
(conformally invariant: notation change from volume 1!) 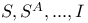
![$\mathfrak{\sigma^{\mathscr{A}}}[P]$](/math_tex/c35882b63f27cd3b10259873d9c3c78182.gif) ,
, ![$\mathfrak{\sigma^{\mathscr{A}}}[\mathscr{U}]$](/math_tex/c4d1e37b68cb51325a3a0b8c02e3b97e82.gif)
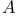 (anti-Einstein)
(anti-Einstein) 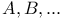 (clumped indices)
(clumped indices) 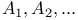 (similarly clumped indices)
(similarly clumped indices) 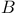 (BMS group)
(BMS group) 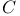 (complex conjugation)
(complex conjugation) 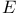 (Einstein cylinder)
(Einstein cylinder) 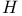 (hypersurface)
(hypersurface) 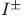 ,
, 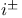 ,
, 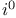
 (null cone in
(null cone in 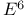 )
) 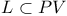 (quadric in projective space)
(quadric in projective space) 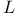 (labelling set)
(labelling set) 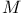 (manifold, space-time)
(manifold, space-time) 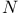 (null volume 3-form)
(null volume 3-form) 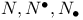 (space of rays in
(space of rays in 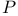 (Poincare group)
(Poincare group) 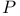 (Minkowski 3-space)
(Minkowski 3-space) 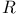 (Lorentz rotations)
(Lorentz rotations) 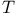 (translations)
(translations) 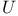 (super translations)
(super translations) 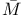 (manifold-with-boundary)
(manifold-with-boundary) 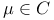 (ray of null congruence)
(ray of null congruence) 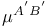 (angular momentum spinor)
(angular momentum spinor)  (covariant derivative)
(covariant derivative)  (function on
(function on 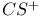 ),
), 
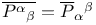
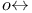 (origin-dependent correspondence)
(origin-dependent correspondence) 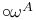 ,
, 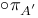 (constant spinors)
(constant spinors) 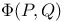 (squared interval)
(squared interval) 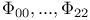 (Ricci spinor components)
(Ricci spinor components) 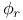 (components of massless field)
(components of massless field) 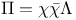
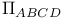 (Plebanski spinor)
(Plebanski spinor) 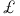 (Lie derivative)
(Lie derivative) 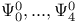 (Weyl components at
(Weyl components at 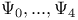 (Weyl spinor components)
(Weyl spinor components) 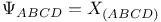 (Weyl spinor)
(Weyl spinor) 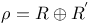 (spinor abstract indices reduced)
(spinor abstract indices reduced) 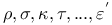 (spin coefficients)
(spin coefficients)  (symplectic invariant)
(symplectic invariant) 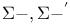 generator (on
generator (on ![$\sigma...(...)...,\sigma...[...]...$](/math_tex/f4b9e2800800dac11e7e8955a1aba45d82.gif)
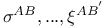 ,... (primary parts)
,... (primary parts) 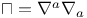 (D'Alembertian)
(D'Alembertian) 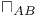 ,
, 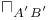 (spinor commutator)
(spinor commutator) 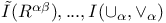 (infinity functions)
(infinity functions) 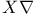 (directional derivative)
(directional derivative) 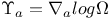
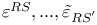
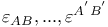
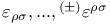 ,
, 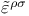
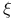 (holomorphic coordinate for
(holomorphic coordinate for 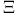 (Witten 2-form)
(Witten 2-form)  (complex stereographic coordinate)
(complex stereographic coordinate) 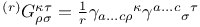
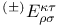 ,
, 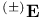
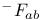 ,
, 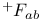
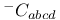 ,
, 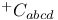 ,
, 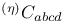
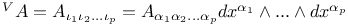 (p-form)
(p-form) 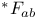 ,
, 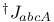 ,
, 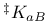 (duals)
(duals) 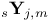 (basis for harmonics)
(basis for harmonics)  (lightface sloping indices: abstract)
(lightface sloping indices: abstract)