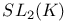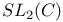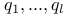|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Carter R.W. — Simple groups of Lie type |
|
|
 |
| Предметный указатель |
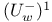 , the subgroup , the subgroup 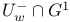 of a twisted group of a twisted group 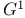 229 229
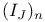 , the set of homogeneous polynomials in , the set of homogeneous polynomials in 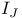 of degree n 140 of degree n 140
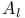 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
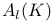 , the Chevalley group of type , the Chevalley group of type 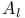 over K 64 over K 64
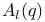 , the Chevalley group of type , the Chevalley group of type 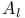 over GF(q) 121 over GF(q) 121
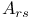 , the Cartan integer associated with a pair of roots 38 , the Cartan integer associated with a pair of roots 38
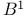 , the subgroup , the subgroup 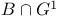 of a twisted group of a twisted group 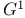 230 230
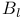 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
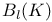 , the Chevalley group of type , the Chevalley group of type 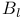 over K 64 over K 64
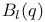 , the Chevalley group of type , the Chevalley group of type 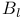 over GF(q) 121 over GF(q) 121
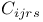 , the constants occurring in Chevalley's commutator formula 77 , the constants occurring in Chevalley's commutator formula 77
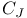 , the element of the Coxeter complex associated with a set J of fundamental roots 31 , the element of the Coxeter complex associated with a set J of fundamental roots 31
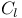 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
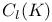 , the Chevalley group of type , the Chevalley group of type 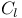 over K 64 over K 64
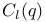 , the Chevalley group of type , the Chevalley group of type 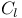 over GF(q) 121 over GF(q) 121
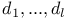 , the degrees of the basic polynomial invariants of W 130 , the degrees of the basic polynomial invariants of W 130
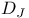 , the set of distinguished coset representatives of , the set of distinguished coset representatives of 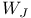 in W 29 in W 29
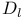 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
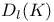 , the Chevalley group of type , the Chevalley group of type 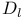 over K 64 over K 64
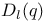 , the Chevalley group of type , the Chevalley group of type 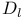 over GF(q) 121 over GF(q) 121
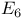 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
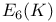 , the Chevalley group of type , the Chevalley group of type 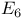 over K 64 over K 64
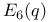 , the Chevalley group of type , the Chevalley group of type 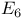 over GF(q) 121 over GF(q) 121
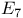 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
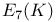 , the Chevalley group of type , the Chevalley group of type 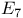 over K 64 over K 64
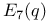 , the Chevalley group of type , the Chevalley group of type 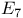 over GF(q) 121 over GF(q) 121
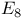 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
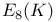 , the Chevalley group of type , the Chevalley group of type 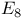 over K 64 over K 64
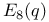 , the Chevalley group of type , the Chevalley group of type 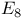 over GF(q) 121 over GF(q) 121
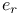 , a root vector in a simple Lie algebra 51 , a root vector in a simple Lie algebra 51
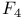 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
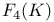 , the Chevalley group of type , the Chevalley group of type 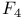 over K 64 over K 64
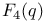 , the Chevalley group of type , the Chevalley group of type 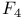 over GF(q) 121 over GF(q) 121
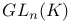 , the general linear group of degree n over K 2 , the general linear group of degree n over K 2
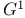 , a twisted group 226 , a twisted group 226
 , the type of a simple Lie algebra over , the type of a simple Lie algebra over  43 43
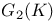 , the Chevalley group of type , the Chevalley group of type  over over 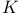 64 64
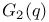 , the Chevalley group of type , the Chevalley group of type  over GF(q) 121 over GF(q) 121
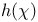 , the automorphism of the Lie algebra , the automorphism of the Lie algebra 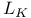 determined by a K-character determined by a K-character  of P 98 of P 98
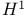 , the diagonal subgroup , the diagonal subgroup 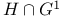 of a twisted group of a twisted group 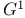 226 226
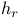 , the co-root associated to a root r 42 , the co-root associated to a root r 42
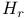 , the hyperplane orthogonal to a root r 20 , the hyperplane orthogonal to a root r 20
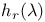 , the element of H associated with a root r and an element , the element of H associated with a root r and an element  of K 92 of K 92
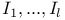 , a set of basic polynomial invariants of the Weyl group W 126 , a set of basic polynomial invariants of the Weyl group W 126
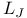 , a Levi subgroup of a parabolic subgroup , a Levi subgroup of a parabolic subgroup 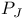 119 119
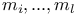 the exponents of the Weyl group 155 the exponents of the Weyl group 155
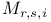 , the integer , the integer 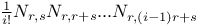 61 61
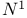 , the monomial subgroup , the monomial subgroup 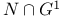 of a twisted group of a twisted group 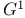 226 226
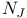 , the inverse image in N of the subgroup , the inverse image in N of the subgroup 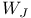 of W 108 of W 108
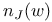 , the number of elements fixed by w in the W-orbit containing , the number of elements fixed by w in the W-orbit containing 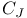 of the Coxeter complex 136 of the Coxeter complex 136
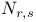 , the structure constant of a simple Lie algebra determined by a pair of roots 52 , the structure constant of a simple Lie algebra determined by a pair of roots 52
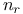 , the generator , the generator 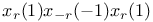 of N 93 of N 93
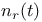 , the element , the element 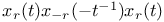 of N 96 of N 96
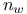 , an element of N mapping to w in W 115 , an element of N mapping to w in W 115
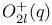 , the orthogonal group of degree 2l over GF(q) leaving invariant a quadratic form of index l 6 , the orthogonal group of degree 2l over GF(q) leaving invariant a quadratic form of index l 6
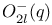 , the orthogonal group of degree 2l over GF(q) leaving invariant a quadratic form of index l-1 6 , the orthogonal group of degree 2l over GF(q) leaving invariant a quadratic form of index l-1 6
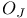 , the number of , the number of  -orbits in a -orbits in a  -invariant set J of fundamental roots 254 -invariant set J of fundamental roots 254
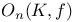 , the orthogonal group of degree n over K leaving invariant the quadratic form f 4 , the orthogonal group of degree n over K leaving invariant the quadratic form f 4
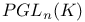 , the projective general linear group of degree n over K 2 , the projective general linear group of degree n over K 2
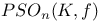 , the projective special orthogonal group of degree n over K leaving invariant the quadratic form f 5 , the projective special orthogonal group of degree n over K leaving invariant the quadratic form f 5
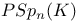 , the projective symplectic group of degree n over K 4 , the projective symplectic group of degree n over K 4
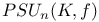 , the projective special unitary group of degree n over K leaving invariant the Hermitian form f 7 , the projective special unitary group of degree n over K leaving invariant the Hermitian form f 7
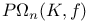 , the projective group of the commutator subgroup , the projective group of the commutator subgroup 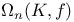 of of 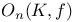 5 5
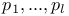 , a system of fundamental roots 38 , a system of fundamental roots 38
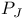 , the parabolic subgroup , the parabolic subgroup 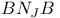 associated with a set J of fundamental roots 108 associated with a set J of fundamental roots 108
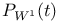 , the polynomial , the polynomial 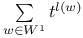 254 254
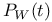 , the polynomial , the polynomial 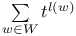 135 135
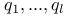 , the fundamental weights of a simple Lie algebra 98 , the fundamental weights of a simple Lie algebra 98
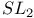 67 81 87 88 67 81 87 88
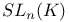 , the special linear group of degree n over K 2 , the special linear group of degree n over K 2
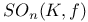 , the special orthogonal group of degree n over K leaving invariant the quadratic form f 5 , the special orthogonal group of degree n over K leaving invariant the quadratic form f 5
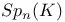 , the symplectic group of degree n over K 2 , the symplectic group of degree n over K 2
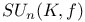 , the special unitary group of degree n over K leaving invariant the Hermitian form f 7 , the special unitary group of degree n over K leaving invariant the Hermitian form f 7
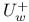 , the product of the root subgroups corresponding to positive roots transformed by w into positive roots 115 , the product of the root subgroups corresponding to positive roots transformed by w into positive roots 115
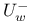 , the product of the root subgroups corresponding to positive roots transformed by w into negative roots 115 , the product of the root subgroups corresponding to positive roots transformed by w into negative roots 115
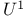 , the unipotent subgroup , the unipotent subgroup 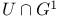 of a twisted group of a twisted group 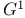 226 226
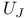 , the unipotent radical of the parabolic subgroup , the unipotent radical of the parabolic subgroup 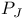 119 119
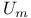 , the subgroup of U generated by the root subgroups corresponding to roots of height at least m 78 , the subgroup of U generated by the root subgroups corresponding to roots of height at least m 78
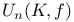 , the unitary group of degree n over K leaving invariant the Hermitian form f 7 , the unitary group of degree n over K leaving invariant the Hermitian form f 7
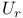 , the product of the root subgroups corresponding to positive roots other than r 104 , the product of the root subgroups corresponding to positive roots other than r 104
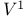 , the unipotent subgroup , the unipotent subgroup 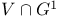 of a twisted group of a twisted group 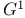 226 226
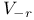 , the product of the root subgroups corresponding to negative roots other than -r 105 , the product of the root subgroups corresponding to negative roots other than -r 105
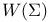 , the group of type-preserving automorphisms of the abstract Coxeter group , the group of type-preserving automorphisms of the abstract Coxeter group  284 284
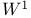 , the subgroup of elements of W commuting with the isometry , the subgroup of elements of W commuting with the isometry  217 217
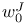 , the element of , the element of 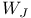 which transforms every positive root in which transforms every positive root in 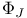 to a negative root 218 to a negative root 218
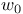 , the element of W which transforms each positive root to a negative root 20 , the element of W which transforms each positive root to a negative root 20
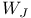 , the subgroup of W generated by the fundamental reflections , the subgroup of W generated by the fundamental reflections 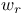 for r in J 27 for r in J 27
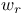 , the reflection in the hyperplane orthogonal to the root r 12 , the reflection in the hyperplane orthogonal to the root r 12
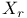 , the root subgroup of a Chevalley group corresponding to the root r 68 , the root subgroup of a Chevalley group corresponding to the root r 68
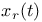 , the generator exp (t ad , the generator exp (t ad 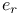 ) of a Chevalley group 64 ) of a Chevalley group 64
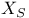 , the subgroup of a Chevalley group generated by the root subgroups corresponding to roots in S 227 , the subgroup of a Chevalley group generated by the root subgroups corresponding to roots in S 227
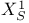 , the root subgroup , the root subgroup 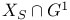 of a twisted group of a twisted group 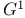 227 227
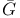 , the universal Chevalley group associated with G 190 , the universal Chevalley group associated with G 190
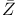 , the centre of the universal Chevalley group , the centre of the universal Chevalley group 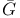 190 190
 , a K-character of P 97 , a K-character of P 97
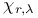 , the K-character of P taking value , the K-character of P taking value 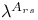 at the root s 48 at the root s 48
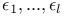 , the eigenvalues of , the eigenvalues of  with eigenvectors with eigenvectors 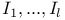 254 254
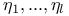 , the eigenvalues of the isometry , the eigenvalues of the isometry  of of 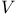 251 251
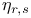 , the integer , the integer 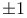 defined by defined by 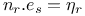 , , 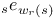 93 93
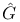 , the extension of G by its group of diagonal automorphisms 118 , the extension of G by its group of diagonal automorphisms 118
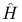 , the group of automorphisms , the group of automorphisms 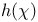 of of 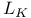 98 98
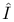 , the set of alternating polynomials on , the set of alternating polynomials on 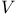 139 139
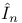 , the set of homogeneous alternating polynomials of degree n 140 , the set of homogeneous alternating polynomials of degree n 140
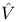 , the dual space of , the dual space of 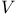 123 123
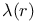 , an integer which takes value 1 if r is a short root and 2 or 3 if r is a long root 204 206 , an integer which takes value 1 if r is a short root and 2 or 3 if r is a long root 204 206
 , the complex field 34 , the complex field 34
 , the field of rationals 153 , the field of rationals 153
 , the real number field 12 , the real number field 12
 , the ring of rational integers 50 , the ring of rational integers 50
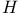 , a Cartan subalgebra of a simple Lie algebra 35 , a Cartan subalgebra of a simple Lie algebra 35
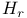 , the 1-dimensional subspace of , the 1-dimensional subspace of 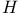 containing containing 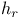 83 83
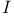 , the ring of polynomial invariants of a Weyl group W 124 , the ring of polynomial invariants of a Weyl group W 124
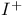 , the set of polynomials in , the set of polynomials in 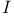 with no constant term 125 with no constant term 125
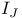 , the set of polynomials on , the set of polynomials on 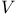 invariant under invariant under 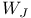 140 140
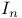 , the set of homogeneous polynomials in , the set of homogeneous polynomials in 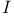 of degree n 132 of degree n 132
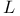 , a Lie algebra, usually simple over , a Lie algebra, usually simple over  33 33
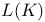 , the Chevalley group of type , the Chevalley group of type 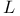 over K 64 over K 64
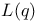 , the Chevalley group of type , the Chevalley group of type 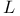 over GF(q) 121 over GF(q) 121
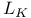 , the Lie algebra over K constructed from the simple Lie algebra , the Lie algebra over K constructed from the simple Lie algebra 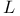 over over  62 62
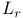 , the 1-dimensional subspace of , the 1-dimensional subspace of 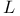 corresponding to the root r 36 corresponding to the root r 36
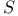 , the algebra of polynomial functions on , the algebra of polynomial functions on 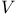 123 123
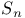 , the set of homogeneous polynomials in , the set of homogeneous polynomials in 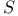 of degree n 132 of degree n 132
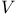 , a vector space 2 , a vector space 2
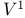 , the set of elements of , the set of elements of 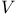 invariant under the isometry invariant under the isometry  217 217
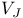 , the subspace of , the subspace of 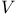 spanned by a set J of fundamental roots 27 spanned by a set J of fundamental roots 27
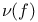 , the Witt index of a form f 5 , the Witt index of a form f 5
 , a building 292 , a building 292
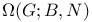 , the building associated with a group G with (B, N)-pair 293 , the building associated with a group G with (B, N)-pair 293
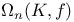 , the commutator subgroup of the orthogonal group , the commutator subgroup of the orthogonal group 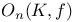 5 5
 , a root system 12 , a root system 12
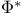 , the set of co-roots of roots in , the set of co-roots of roots in  49 49
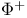 , the set of positive roots in , the set of positive roots in  14 14
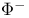 , the set of negative roots in , the set of negative roots in  16 16
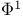 , the set of projections on to , the set of projections on to 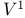 of roots in of roots in  219 219
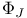 , the set of roots in , the set of roots in  which lie in the subspace which lie in the subspace 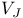 27 27
 , a fundamental system of roots 13 , a fundamental system of roots 13
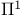 , the set of projections on to , the set of projections on to 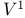 of roots in of roots in  219 219
 , a symmetry of the Dynkin diagram 200 , a symmetry of the Dynkin diagram 200
 , an abstract Coxeter complex 281 , an abstract Coxeter complex 281
 , an automorphism of a Chevalley group obtained by combining a graph and a field automorphism 225 , an automorphism of a Chevalley group obtained by combining a graph and a field automorphism 225
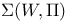 , the abstract Coxeter complex associated with a Weyl group W and fundamental system , the abstract Coxeter complex associated with a Weyl group W and fundamental system  288 288
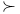 , a total order relation on , a total order relation on 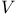 13 13
 , the isometry of , the isometry of 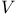 determined by a symmetry determined by a symmetry  of the Dynkin diagram 201 217 of the Dynkin diagram 201 217
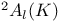 , the twisted group of type , the twisted group of type 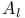 over K 251 over K 251
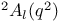 , the twisted group of type , the twisted group of type 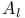 over over 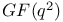 251 251
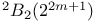 , the twisted Suzuki group of type , the twisted Suzuki group of type 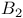 over over 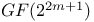 251 251
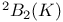 , the twisted Suzuki group of type , the twisted Suzuki group of type 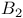 over K 251 over K 251
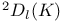 , the twisted orthogonal group of type , the twisted orthogonal group of type 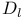 over K 251 over K 251
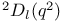 , the twisted orthogonal group of type , the twisted orthogonal group of type 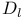 over over 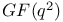 251 251
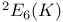 , the twisted group of type , the twisted group of type 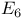 over K 251 over K 251
| 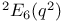 , the twisted group of type , the twisted group of type 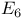 over over 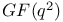 251 251
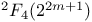 , the twisted Ree group of type , the twisted Ree group of type 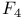 over over 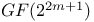 251 251
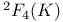 , the twisted Ree group of type , the twisted Ree group of type 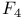 over K 251 over K 251
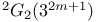 , the twisted Ree group of type , the twisted Ree group of type  over over 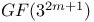 251 251
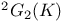 , the twisted Ree group of type , the twisted Ree group of type  over K 251 over K 251
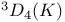 , the triality twisted group of type , the triality twisted group of type 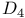 over K 251 over K 251
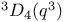 , the triality twisted group of type , the triality twisted group of type 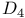 over over 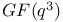 251 251
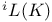 , the twisted group constructed from a Chevalley group , the twisted group constructed from a Chevalley group 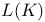 by means of a symmetry of order i 251 by means of a symmetry of order i 251
(B,N)-pair 107—114 294
(B,N)-pair in twisted groups 227 230
(B,N)-pair, operating on a building 299 302
A, the rational group algebra of e(Q) 148
Abstract Coxeter complex 281 284 288 291 296
ad x, the adjoint map of left multiplication by the element x in a Lie algebra 34
Adjacent chambers 276
Adjoint Chevalley group 198
Alternating elements 148
Alternating polynomials 139
apartments 292 296
Automorphisms, of Chevalley groups 199 211
Automorphisms, of simple Lie algebras 60 63
B, the subgroup UH of a Chevalley group 104
Basic polynomial invariants 128 129
Betti numbers 169
Borel subgroup 104
Bruhat decomposition 104 106 109
Building 292 296 302
Building, associated with a group with (B,N)-pair 293
C, a chamber 21
Canonical form, for elements of a Chevalley group 115 117
Canonical form, for elements of a twisted group 229
Canonical form, for elements of a unipotent subgroup 78
Cartan decomposition 35
Cartan matrix 43—45 99 122
Central series of unipotent group 78
Chamber 21—23 275
Chamber complex 275
Chevalley basis 56
Chevalley group, definition 64
Chevalley's theorems, on commutator formula 76
Chevalley's theorems, on existence of integral basis 56
Chevalley's theorems, on polynomial invariants 128
Classification of simple Lie algebras 43
Closed set of roots 114
Co-roots 49
Coleman's theorem 166
Commutator formula 76
COMPLEX 274
Conway groups 308
Coxeter complex 30—32 136 137 255 288
Coxeter element 156
Coxeter group 25 284 286 292
Coxeter's theorem 156
Degrees of basic invariants 130—133 145 155
Derivations 34 61
Diagonal automorphism 200
Diagonal subgroup H, of a Chevalley group 97 99 117
Diagonal subgroup H, of a twisted group 238 244
Dihedral subgroup of Weyl group 158 161
Distinguished coset representatives 30 138
Double coset decomposition 109 110
Dual root system 49 50
Duality of exponents 156 168
Dynkin diagram, of a simple Lie algebra 40
Dynkin diagram, of the twisted groups 224
e(Q), a multiplicative group isomorphic to the additive group Q 148
Eigenvalues of Coxeter element 165 166 168
Elementary symmetric polynomials 124
Existence theorem for simple Lie algebras 42
Exponential map 60 66
Exponents of Weyl group 169
Extraspecial pair of roots 58
Factorization of the polynomial 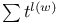 , in Chevalley groups 135 , in Chevalley groups 135
Factorization of the polynomial 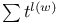 , in twisted groups 254 , in twisted groups 254
Field automorphism 200
Finite Chevalley groups 120—122
Finite twisted groups 251
Fischer groups 309
Folding 277
Frobenius — Perron theorem 162
Fundamental group 99
Fundamental reflection 17
Fundamental system of roots 13 19 21
Fundamental weights 98 146 148
G', the commutator subgroup (derived group) of G 170
G, a group, usually a Chevalley group 68
gallery 276
Generators and relations, for Chevalley group 190
Generators and relations, for Weyl group 23 25
GF(q), the Galois field with q elements 2
Graph automorphism, of the group 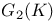 206 206
Graph automorphism, of the groups 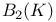 , , 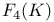 204 204
h(r), the height of a root r 16
H, the diagonal subgroup of a Chevalley group G 97
Height of a root 16 77 153—155
Held group 306
Higman — Sims group 307
Homomorphism, from 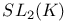 88 88
Homomorphism, from 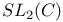 87 87
Ideal of Lie algebra 33
Induced character 136
Isomorphism theorem for simple Lie algebras 42
J, a subset of the set  of fundamental roots 27 of fundamental roots 27
Jacobi identity 33
Jacobian 134 166
Janko groups 305
K*, the multiplicative group of non-zero elements of K 97
K, a field 2
K-character 97 99 121 199
K-character, self-conjugate 238
Killing form 34
l(w), the length of an element w of the Weyl group 18
l, the rank of a simple Lie algebra 35
Leech lattice 308
Lefshetz fixed point formula 169
length function 18 136
Levi decomposition 118
Levi subgroup 119
Lie algebra, definition 33
Linear groups 2 184 185
Lyons group 306
Macdonald's theorem 151
Mathieu groups 303
Matsumoto's Theorem 286
McLaughlin group 307
Monomial subgroup N, of Chevalley group 101
Monomial subgroup N, of twisted group 228
Monomial subgroup N, relationship to Weyl group 102
Morphism of chamber complexes 276
N, the monomial subgroup of a Chevalley group G 101
N, the number of positive roots 43
Nilpotent derivations 61 66 69
Nilpotent Lie algebra 35
Opposite folding 280
Order, of Coxeter elements 163 168
Order, of finite Chevalley groups 122
Order, of finite twisted groups 253 259 262
Order, of sporadic simple groups 310
Ordering of vector space 13
Orthogonal groups 4—8 184—188 271
P, the additive group generated by 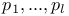 97 97
Parabolic subgroups, of a Chevalley group 118 119
Parabolic subgroups, of a group with (B,N)-pair 111—113
Parabolic subgroups, of a twisted group 231
Parabolic subgroups, of a Weyl group 27—30 32
Poincare polynomial 169
Polynomial invariants of Weyl group 123
Positive systems of roots 13
Q, the additive group generated by 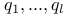 99 99
R, the root of maximum height 156
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



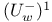 , the subgroup
, the subgroup 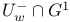 of a twisted group
of a twisted group 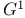
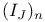 , the set of homogeneous polynomials in
, the set of homogeneous polynomials in 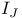 of degree n
of degree n 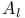 , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 
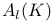 , the Chevalley group of type
, the Chevalley group of type 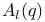 , the Chevalley group of type
, the Chevalley group of type 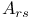 , the Cartan integer associated with a pair of roots
, the Cartan integer associated with a pair of roots 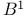 , the subgroup
, the subgroup 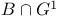 of a twisted group
of a twisted group 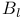 , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 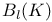 , the Chevalley group of type
, the Chevalley group of type 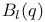 , the Chevalley group of type
, the Chevalley group of type 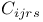 , the constants occurring in Chevalley's commutator formula
, the constants occurring in Chevalley's commutator formula 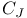 , the element of the Coxeter complex associated with a set J of fundamental roots
, the element of the Coxeter complex associated with a set J of fundamental roots 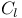 , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 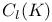 , the Chevalley group of type
, the Chevalley group of type 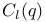 , the Chevalley group of type
, the Chevalley group of type 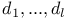 , the degrees of the basic polynomial invariants of W
, the degrees of the basic polynomial invariants of W 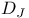 , the set of distinguished coset representatives of
, the set of distinguished coset representatives of 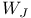 in W
in W 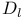 , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 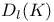 , the Chevalley group of type
, the Chevalley group of type 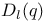 , the Chevalley group of type
, the Chevalley group of type 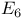 , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 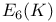 , the Chevalley group of type
, the Chevalley group of type 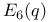 , the Chevalley group of type
, the Chevalley group of type 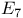 , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 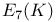 , the Chevalley group of type
, the Chevalley group of type 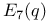 , the Chevalley group of type
, the Chevalley group of type 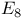 , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 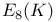 , the Chevalley group of type
, the Chevalley group of type 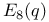 , the Chevalley group of type
, the Chevalley group of type 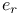 , a root vector in a simple Lie algebra
, a root vector in a simple Lie algebra 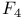 , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 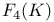 , the Chevalley group of type
, the Chevalley group of type 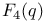 , the Chevalley group of type
, the Chevalley group of type 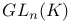 , the general linear group of degree n over K
, the general linear group of degree n over K  , the type of a simple Lie algebra over
, the type of a simple Lie algebra over 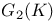 , the Chevalley group of type
, the Chevalley group of type 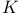
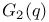 , the Chevalley group of type
, the Chevalley group of type 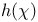 , the automorphism of the Lie algebra
, the automorphism of the Lie algebra 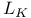 determined by a K-character
determined by a K-character  of P
of P 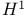 , the diagonal subgroup
, the diagonal subgroup 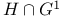 of a twisted group
of a twisted group 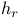 , the co-root associated to a root r
, the co-root associated to a root r 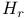 , the hyperplane orthogonal to a root r
, the hyperplane orthogonal to a root r 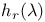 , the element of H associated with a root r and an element
, the element of H associated with a root r and an element  of K
of K 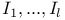 , a set of basic polynomial invariants of the Weyl group W
, a set of basic polynomial invariants of the Weyl group W 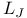 , a Levi subgroup of a parabolic subgroup
, a Levi subgroup of a parabolic subgroup 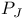
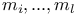 the exponents of the Weyl group
the exponents of the Weyl group 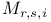 , the integer
, the integer 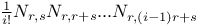
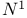 , the monomial subgroup
, the monomial subgroup 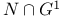 of a twisted group
of a twisted group 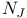 , the inverse image in N of the subgroup
, the inverse image in N of the subgroup 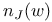 , the number of elements fixed by w in the W-orbit containing
, the number of elements fixed by w in the W-orbit containing 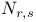 , the structure constant of a simple Lie algebra determined by a pair of roots
, the structure constant of a simple Lie algebra determined by a pair of roots 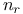 , the generator
, the generator 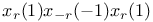 of N
of N 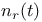 , the element
, the element 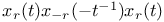 of N
of N 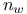 , an element of N mapping to w in W
, an element of N mapping to w in W 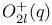 , the orthogonal group of degree 2l over GF(q) leaving invariant a quadratic form of index l
, the orthogonal group of degree 2l over GF(q) leaving invariant a quadratic form of index l 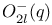 , the orthogonal group of degree 2l over GF(q) leaving invariant a quadratic form of index l-1
, the orthogonal group of degree 2l over GF(q) leaving invariant a quadratic form of index l-1 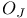 , the number of
, the number of  -orbits in a
-orbits in a 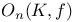 , the orthogonal group of degree n over K leaving invariant the quadratic form f
, the orthogonal group of degree n over K leaving invariant the quadratic form f 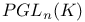 , the projective general linear group of degree n over K
, the projective general linear group of degree n over K 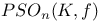 , the projective special orthogonal group of degree n over K leaving invariant the quadratic form f
, the projective special orthogonal group of degree n over K leaving invariant the quadratic form f 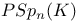 , the projective symplectic group of degree n over K
, the projective symplectic group of degree n over K 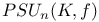 , the projective special unitary group of degree n over K leaving invariant the Hermitian form f
, the projective special unitary group of degree n over K leaving invariant the Hermitian form f 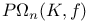 , the projective group of the commutator subgroup
, the projective group of the commutator subgroup 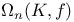 of
of 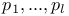 , a system of fundamental roots
, a system of fundamental roots 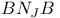 associated with a set J of fundamental roots
associated with a set J of fundamental roots 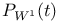 , the polynomial
, the polynomial 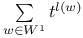
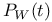 , the polynomial
, the polynomial 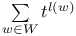
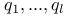 , the fundamental weights of a simple Lie algebra
, the fundamental weights of a simple Lie algebra 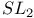
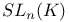 , the special linear group of degree n over K
, the special linear group of degree n over K 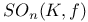 , the special orthogonal group of degree n over K leaving invariant the quadratic form f
, the special orthogonal group of degree n over K leaving invariant the quadratic form f 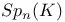 , the symplectic group of degree n over K
, the symplectic group of degree n over K 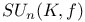 , the special unitary group of degree n over K leaving invariant the Hermitian form f
, the special unitary group of degree n over K leaving invariant the Hermitian form f 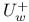 , the product of the root subgroups corresponding to positive roots transformed by w into positive roots
, the product of the root subgroups corresponding to positive roots transformed by w into positive roots 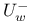 , the product of the root subgroups corresponding to positive roots transformed by w into negative roots
, the product of the root subgroups corresponding to positive roots transformed by w into negative roots 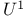 , the unipotent subgroup
, the unipotent subgroup 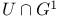 of a twisted group
of a twisted group 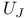 , the unipotent radical of the parabolic subgroup
, the unipotent radical of the parabolic subgroup 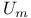 , the subgroup of U generated by the root subgroups corresponding to roots of height at least m
, the subgroup of U generated by the root subgroups corresponding to roots of height at least m 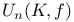 , the unitary group of degree n over K leaving invariant the Hermitian form f
, the unitary group of degree n over K leaving invariant the Hermitian form f 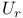 , the product of the root subgroups corresponding to positive roots other than r
, the product of the root subgroups corresponding to positive roots other than r 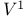 , the unipotent subgroup
, the unipotent subgroup 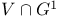 of a twisted group
of a twisted group 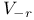 , the product of the root subgroups corresponding to negative roots other than -r
, the product of the root subgroups corresponding to negative roots other than -r 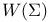 , the group of type-preserving automorphisms of the abstract Coxeter group
, the group of type-preserving automorphisms of the abstract Coxeter group 
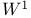 , the subgroup of elements of W commuting with the isometry
, the subgroup of elements of W commuting with the isometry 
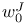 , the element of
, the element of 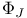 to a negative root
to a negative root 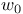 , the element of W which transforms each positive root to a negative root
, the element of W which transforms each positive root to a negative root 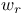 for r in J
for r in J 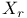 , the root subgroup of a Chevalley group corresponding to the root r
, the root subgroup of a Chevalley group corresponding to the root r 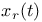 , the generator exp (t ad
, the generator exp (t ad 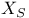 , the subgroup of a Chevalley group generated by the root subgroups corresponding to roots in S
, the subgroup of a Chevalley group generated by the root subgroups corresponding to roots in S 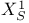 , the root subgroup
, the root subgroup 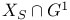 of a twisted group
of a twisted group 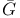 , the universal Chevalley group associated with G
, the universal Chevalley group associated with G 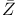 , the centre of the universal Chevalley group
, the centre of the universal Chevalley group 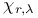 , the K-character of P taking value
, the K-character of P taking value 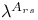 at the root s
at the root s 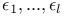 , the eigenvalues of
, the eigenvalues of 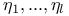 , the eigenvalues of the isometry
, the eigenvalues of the isometry 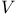
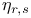 , the integer
, the integer 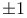 defined by
defined by 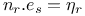 ,
, 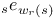
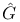 , the extension of G by its group of diagonal automorphisms
, the extension of G by its group of diagonal automorphisms 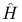 , the group of automorphisms
, the group of automorphisms 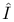 , the set of alternating polynomials on
, the set of alternating polynomials on 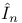 , the set of homogeneous alternating polynomials of degree n
, the set of homogeneous alternating polynomials of degree n 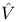 , the dual space of
, the dual space of 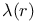 , an integer which takes value 1 if r is a short root and 2 or 3 if r is a long root
, an integer which takes value 1 if r is a short root and 2 or 3 if r is a long root  , the field of rationals
, the field of rationals  , the real number field
, the real number field  , the ring of rational integers
, the ring of rational integers 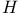 , a Cartan subalgebra of a simple Lie algebra
, a Cartan subalgebra of a simple Lie algebra 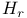 , the 1-dimensional subspace of
, the 1-dimensional subspace of 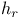
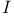 , the ring of polynomial invariants of a Weyl group W
, the ring of polynomial invariants of a Weyl group W 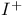 , the set of polynomials in
, the set of polynomials in 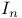 , the set of homogeneous polynomials in
, the set of homogeneous polynomials in 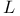 , a Lie algebra, usually simple over
, a Lie algebra, usually simple over 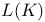 , the Chevalley group of type
, the Chevalley group of type 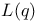 , the Chevalley group of type
, the Chevalley group of type 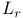 , the 1-dimensional subspace of
, the 1-dimensional subspace of 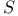 , the algebra of polynomial functions on
, the algebra of polynomial functions on 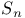 , the set of homogeneous polynomials in
, the set of homogeneous polynomials in 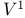 , the set of elements of
, the set of elements of 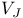 , the subspace of
, the subspace of 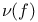 , the Witt index of a form f
, the Witt index of a form f  , a building
, a building 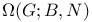 , the building associated with a group G with (B, N)-pair
, the building associated with a group G with (B, N)-pair  , a root system
, a root system 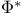 , the set of co-roots of roots in
, the set of co-roots of roots in 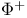 , the set of positive roots in
, the set of positive roots in 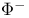 , the set of negative roots in
, the set of negative roots in 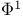 , the set of projections on to
, the set of projections on to  , a fundamental system of roots
, a fundamental system of roots 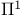 , the set of projections on to
, the set of projections on to  , an automorphism of a Chevalley group obtained by combining a graph and a field automorphism
, an automorphism of a Chevalley group obtained by combining a graph and a field automorphism 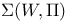 , the abstract Coxeter complex associated with a Weyl group W and fundamental system
, the abstract Coxeter complex associated with a Weyl group W and fundamental system 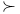 , a total order relation on
, a total order relation on 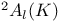 , the twisted group of type
, the twisted group of type 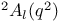 , the twisted group of type
, the twisted group of type 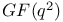
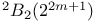 , the twisted Suzuki group of type
, the twisted Suzuki group of type 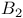 over
over 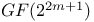
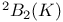 , the twisted Suzuki group of type
, the twisted Suzuki group of type 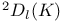 , the twisted orthogonal group of type
, the twisted orthogonal group of type 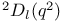 , the twisted orthogonal group of type
, the twisted orthogonal group of type 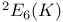 , the twisted group of type
, the twisted group of type 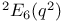 , the twisted group of type
, the twisted group of type 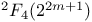 , the twisted Ree group of type
, the twisted Ree group of type 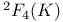 , the twisted Ree group of type
, the twisted Ree group of type 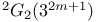 , the twisted Ree group of type
, the twisted Ree group of type 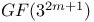
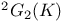 , the twisted Ree group of type
, the twisted Ree group of type 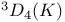 , the triality twisted group of type
, the triality twisted group of type 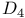 over K
over K 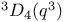 , the triality twisted group of type
, the triality twisted group of type 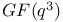
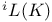 , the twisted group constructed from a Chevalley group
, the twisted group constructed from a Chevalley group 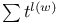 , in Chevalley groups
, in Chevalley groups 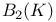 ,
,