Авторизация
Поиск по указателям
Hadlock C.R. — Field theory and its classical problems
Обсудите книгу на научном форуме Нашли опечатку?
Название: Field theory and its classical problemsАвтор: Hadlock C.R. Аннотация: From author: "I wrote this book for myself.
Язык: Рубрика: Математика /Серия: Сделано в холле Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1978Количество страниц: 336Добавлена в каталог: 04.12.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
129 291 Abel, Niels Henrik 5 177 178 Abel, theorem of 165 172 181 Abelian group 138 Adamson, I.T. 179 Affine plane curve 186 Alexanderson, Gerald L. 120 179 Algebraic extension 72 79 80 258 Algebraic numbers 35 Algebraic numbers, countability 39 239 Algebraic numbers, form a field 36 46 80 241 259 Algebraically independent elements 141 211 216 Alternating function 243 Analytic, at a point 185 Analytic, at infinity 185 Analytic, at zero 184 Angles with rational degree measure, constructibility 119 275 Archibald, R.C. 120 Argument of a complex number 87 Artin, E. 127 177 178 179 Automorphisms 128 Automorphisms of 141 290 291 Automorphisms of 141 290 Automorphisms, associativity 130 Automorphisms, commutativity 129 Automorphisms, extensions of 141 290 295 Automorphisms, group of 131 Automorphisms, identity 129 Automorphisms, inverse 130 Basic Hilbert set 210 315 Bell, E.T. 7 Belonging to an exponent modulo p 102 Bieberbach, Ludwig 57 Birkhoff, Garrett 58 179 Bisection of an angle 30 232 Boyer, Carl 7 Brown, James W. 58 220 Cajori, Florian 178 Cancellation property, for polynomials 70 Cancellation property, modulo n 99 Cardano, Girolamo 178 Chain 290 Chain rule 56 247 Churchill, Ruel V. 58 220 Circle in a field 16 Clark, Allan 120 179 Closed 12 Coefficient field 126 Commutator 171 Complementary m-sets 108 Complementary periods 108 Completely reducible 62 Complex conjugate 80 Complex conjugate roots, of polynomials over 80 261 Complex conjugation, automorphism 129 Composition series 152 Congruences 98 Conjugacy, equivalence relation 147 150 294 Conjugacy, of elements 137 Conjugacy, of field extensions 147 294 Conjugacy, of subgroups 147 294 Constructibility 11 57 92 Constructibility and degree 81 Constructibility, compass alone 57 Constructibility, degree condition not sufficient 127 218 282 Constructibility, necessary and sufficient condition 21 94 Constructibility, necessary condition 95 Coset 133 135 284 Courant, Richard 57 Coxeter, H.S.M. 120 Cramer's rule 156 Cubic equation 126 176 177 279 304 Cubic equation, discriminant 177 305 Cubic equation, solvability by real radicals 177 307 Curiosity 24 CYCLE 166 Cyclic group 134 Cyclic group, generator 135 Cyclic group, subgroups 136 286 Cyclotomic polynomials 96 174 252 Cyclotomic polynomials, Galois group 140 Cyclotomic polynomials, irreducibility 119 120 277 Dedekind, R. 177 178 Degree, of a field extension 72 Degree, of a polynomial in one variable 34 Degree, of a polynomial in several variables 39 40 Degree, of a simple extension 74 Degree, of a succession of field extensions 78 Degree, of an algebraic number over a field 73 Dehn, Edgar 178 del Ferro, Scipione 5 Delian problem 3 Dense 210 315 Derivatives of complex functions 49 50 55 Diamond, Harold, G. 58 Dickson, L.E. 120 178 Discriminant of a cubic 177 305 Divisibility of polynomials 34 Division algorithm, for 66 70 250 Division algorithm, for polynomials 60 Divisor 61 Doerge, Karl 220 Doubling the cube 2 24 Duarte, F.J. 4 58 e, transcendence of 56 248 Eichler, Martin 220 Eigenvalue 37 Eisenstein irreducibility criterion 64 Elementary symmetric functions 41 Elliptic functions 178 Equivalence relation 99 150 Euclidean algorithm, for 66 70 250 Euclidean algorithm, for polynomials 67 Euler 85 100 Exponential function, complex argument 47 Extension 58 71 72 Extension, algebraic 72 79 258 Extension, degree of 72 Extension, finite 71 75 Extension, multiple 71 72 Extension, normal 141 142 Extension, radical 124 Extension, simple 71 72 Extension, transcendental 72 Factorization into irreducible factors 69 Factorization into irreducible factors, algorithm for 71 255 Fermat primes 97 Fermat's theorem 100 Ferrari, Ludovico 5 Field 12 34 177 Field isomorphism 290 Finite extension 71 75 Finite fields 120 Finkbeiner, Daniel T., II 120 Fixed field, of a group 139 Fixed field, of an automorphism 139 fun 8 Fundamental constructions 9 Fundamental Galois pairing 145 Fundamental theorem of algebra 34 57 Fundamental theorem of calculus 50 247 Fundamental Theorem of Galois Theory 147 149 Fundamental Theorem on Symmetric Functions 41 g.c.d. 66 Gaal, Lisl 179 Galois group 140 Galois group, computation of 164 165 174 178 298 Galois pairing 145 Galois, Evariste 5 177 178 Galois, theorem of 151 152 Gauss, Carl Friedrich 3 57 107 119 120 Gauss, lemma of 62 197 310 Generator 134 Generic polynomial of degree n 216 Goldstein, Larry Joel 179 Greatest common divisor, of polynomials 66 Greek problems 2 9 Group 131 Group, of a field extension 136 Hasse, Helmut 179 Hermes 120 Hermite, C. 178 Herstein, I.N. 179 Hewitt, Edwin 58 Highest term 42 Hilbert set 210 315 Hilbert, David 219 220 Hilbert, irreducibility theorem of 182 198 199 207 Hillman, Abraham P. 120 179 Identity theorem for power series 183 Imaginary part 47 Index of a subgroup 133 Intermediate fields 80 Intermediate fields, finite number 80 150 261 294 Intersection of fields 23 223 Intestinal fortitude 118 Invariant subgroup 147 Irreducibility, of 165 300 Irreducibility, of a polynomial in one variable 61 Irreducibility, of a polynomial in several variables 186 Irreducibility, of cyclotomic polynomials 119 120 277 Irreducibility, over 64 Irreducibility, over 80 261 Irreducible polynomial, no multiple roots 71 178 254 Isomorphism of a field 290 Jacobson, Nathan 58 120 121 K-cycle 167 Kiernan, B. Melvin 7 179 Klein, Felix 58 Kline, Morris 7 178 kronecker 178 Kronecker's criterion 207 210 Kronecker's specialization 204 210 314 Lagrange, Joseph 5 Lagrange, theorem of 132 Landau, Edmund 57 120 121 Lang, Serge 220 Leading coefficient 38 Levinson, Norman 58 220 Lindemann, F. 3 58 Line in a field 16 M-set 108 Mac Lane, Saunders 58 179 Mann, W. Robert 220 McCoy, N.H. 120 Minimal polynomial 73 Modulo n 98 Modulus, of a complex number 55 86 Monic polynomial 38 Multiple extension 71 72 Multiple root 35 Multiple root, derivative at 39 240 Multiple root, impossible for irreducible polynomials 71 178 254 Nering, Evar D. 120 Niven, Ivan 58 120 Normal extension 141 Normal extension, equivalent properties 142 Normal subgroup 147 nth roots of unity 84 Olmsted, John M. 220 Order, modulo n 102 272 Order, of a group 131 Ore, Oysten 6 Period of an m-set 108 Permutation 40 167 Permutation, even and odd 47 242 Permutation, sequence of transpositions 46 242 Pi ( 48 Pierpont, James 178 220 Plane of a field 16 Polar representation 87 Pollard, Harry 58 Polynomial, in one variable 34 Polynomial, in several variables 39 Power series 182 Primes, infinite number 56 248 Primitive polynomial 71 254 Primitive roots modulo p 101 Primitive roots of unity 85 Primitive roots of unity, degree of 91 92 Proper divisor 61 Puiseux expansions 220 Quadratic equation 176 304 Quadratic extension 13 94 Quadrupling the cube 26 232 Quartic equation 126 177 281 307 Quartic equation, resolvent cubic 282 Quintic equation 172 173 301 Quintisection of an angle 31 84 98 233 262 Quotient 60 Radical extension 124 Radius of convergence 182 Rational functions 188 Rational operations 12 Rational roots theorem 39 237 Real part 47 Real point of an algebraic curve 197 313 Reciprocal power series 185 Redheffer, Raymond 58 220 Regular 17-gon, constructibility 113 Regular pentagon, constructibility 98 119 270 273 Regular polygons, constructibility 3 82 92 104 175 Regular polygons, necessary condition for constructibility 97 119 277 Regular polygons, sufficient condition for constructibility 106 Regular values 186 Regular values at infinity 199 Regular values, existence of 187 Relatively prime polynomials 68 Relaxation 80 Remainder 60 Resolvent cubic 282 Robbins, Herbert 57 Robinson, Abraham 120 Root functions 186 Root functions, analytic 190 Root of a polynomial 34 Roots of complex numbers 84 Ruffini, P. 5 177 Seidenberg, A. 220 Simple extension 71 72 Smallest field with a given property 23 223 Smith, David Eugene 7 178 Solution by radicals 4 123 Solutions to problems 8 221 Solvability by radicals 124 126 152 210 218 Solvable equations 174 Solvable groups 152 Splitting field 80 124 142 Splitting field, degree of 126 260 280 Squaring the circle 2 31 55 Steinberg, R. 58 Stewart, Ian 179 Stromberg, Karl 58 Subgroup 132 Symmetric functions, elementary 41 Symmetric functions, fundamental theorem on 41 Symmetric group 169 Symmetric group, not solvable 171 Symmetric group, polynomials with 171 173 174 176 181 220 302 303 304 Symmetric polynomial 40
Реклама
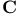, automorphisms of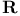 
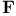
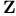
-function ![$\mathbf{Q}[x]$](/math_tex/54467dc30bf2c0753d9715a156c7d6b482.gif)
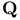
), transcendence of 
|
|
О проекте