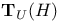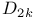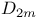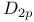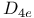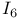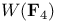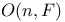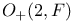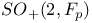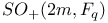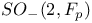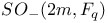Авторизация
Поиск по указателям
Neusel M.D. — Invariant Theory of Finite Groups
Обсудите книгу на научном форуме Нашли опечатку?
Название: Invariant Theory of Finite GroupsАвтор: Neusel M.D. Аннотация: The questions that have been at the center of invariant theory since the 19th century have revolved around the following themes: finiteness, computation, and special classes of invariants. This book begins with a survey of many concrete examples chosen from these themes in the algebraic, homological, and combinatorial context. In further chapters, the authors pick one or the other of these questions as a departure point and present the known answers, open problems, and methods and tools needed to obtain these answers. Chapter 2 deals with algebraic finiteness. Chapter 3 deals with combinatorial finiteness. Chapter 4 presents Noetherian finiteness. Chapter 5 addresses homological finiteness. Chapter 6 presents special classes of invariants, which deal with modular invariant theory and its particular problems and features. Chapter 7 collects results for special classes of invariants and coinvariants such as (pseudo) reflection groups and representations of low degree. If the ground field is finite, additional problems appear and are compensated for in part by the emergence of new tools. One of these is the Steenrod algebra, which the authors introduce in Chapter 8 to solve the inverse invariant theory problem, around which the authors have organized the last three chapters. The book contains numerous examples to illustrate the theory, often of more than passing interest, and an appendix on commutative graded algebra, which provides some of the required basic background. There is an extensive reference list to provide the reader with orientation to the vast literature.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2001Количество страниц: 371Добавлена в каталог: 28.11.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
22 11 11 10 27 75 294 230 101 78 79 195 20 266 174 41 101 266 266 3 3 57 60 137 209 16 74 6 189 248 70 3 2 4 8 3 6 48 2 228 247 61 21 152 247 270 289 21 230 249 248 247 105 248 228 260 275 284 284 157 285 284 285 3 260 266 260 263 243 243 120 318 137 285 248 48 269 48 58 58 168 268 328 79 4 82 80 226 289 156 228 141 13 320 318 15 33 230 57 158 11 11 231 245 267 244 244 259 260 275 23 268 260 260 228 4 4 116 41 33 249 89 61 2-dimensional integer representation 222 3-dimensional integer representation 226 A(n,X,G) 62 Abelian groups 193 Absolutely flat 285 Adem — Wu relations 231 234 Admissible monomial 234 Affine variety 151 168 268 Algebra of coinvariants 8 10 Algebra of invariants 4 Algebraic closure 325 Algebraic finiteness 12 29 Algebraically closed 266 Alternating group 17 27 75 209 211 Alternating polynomials 5 Arrangement of hyperplanes 160 Artin — Rees lemma 249 Associated partition 69 Associated prime 137 328 Associated prime of a module 137 328 Atiyah — Bott fixed-point theorem 50 Augmentation homomorphism 9 Augmentation ideal 8 317 Augmentations homomorphism 317 Auslander — Buchsbaum equality 19 251 Averaging map 47 Averaging operator 151 Bar construction 174 298 Basic monomials 234 Be warned 318 Bigrade 174 Bigraded 316 Bigrading 116 Bireflections 146 308 Block Chern classes 98 BLOCKS 89 Borel group 216 Bottom orbit Chern class 79 Bounded below 45 Brauer lift 49 Brown — Gitler module 248 Bullett — Macdonald identity 231 Burnside's Lemma 60 Cartan formulae 229 Category of graded A-modules 118 Cauchy — Frobenius proposition 60 Center 209 Central series 210 CHARACTER 146 Character field 187 Character theory 194 Characteristic 0 lift 49 Chern class, top 79 Chevalley, C. 190 Class equation 57 Class of nilpotency 210 Classical groups 216 Classical invariant theory 2 Codimension 129 139 247 Codimension of a module 139 Codimension of an algebra 139 Cofactor matrix 126 Cohen — Macaulay 19 21 25 146 193 213 326 Cohen — Macaulay algebra 278 Cohen — Macaulay algebras 115 Cohen — Macaulay property 129 Cohen — Seidenberg relations 268 320 322 Coherent 32 Cohomological finiteness 18 Cohomology of a group with coefficients in a Koszul complex 174 Cohomology of cyclic group 177 Coinvariant 177 Coinvariants 8 9 32 194 Coinvariants of pseudoreflection groups 194 Combinatorial finiteness 14 45 Complete flag 110 164 Complete intersection 20 146 Complete intersections and stabilizer subgroups 307 Complex pseudoreflection groups 187 Component 316 Component of 285 Component of 284 Composite Functor Theorem 174 Concentrated in degree 0 318 Configuration of hyperplanes 103 267 270 Configuration of lines 103 Congruence semigroup lemma 206 Connected graded algebra 317 Conormal sequence 304 Contraction 268 Contravariant variable 174 Converges to 175 Covariant variable 174 Coxeter group 17 212 Coxeter groups 187 Coxeter, H.S.M. 187 Cramer's rule 126 Criterion of D. Bourguiba and S. Zarati 22 Cyclic group 42 65 207 Cyclotomic algebra 48 Cyclotomic integers 48 D(M) 69 Dade bases 99 Dade basis 31 100 173 Dade's condition 100 Dade's construction 18 Dade, E. 18 Dedekind's Lemma 34 Defined over 48 deg(-) 105 deg(A|C) 203 Degree 203 Degree bounds 310 Degree of a module 105 Degree of a monomial 3 Degree of a ring 105 Degree Theorem 105 Degree-zero component 285 294 Delta function basis 79 Delta functions 79 Depth 18 19 Depth and stabilizer subgroups 307 Depth conjecture 21 247 Depth of an algebra 129 Derivation Lemma 327 Di-cyclic group 131 216 Diagonalizable 195 Dickson algebra 21 139 152 225 255 271 Dickson algebra of degree 2 80 Dickson polynomial 21 213 Dickson polynomial, top 155 Dickson polynomials 105 153 173 225 Dickson, L.E. 156 Differential 116 Dihedral group 50 82 108 127 218 219 Dihedral group of order 2p 11 Dimension, global 118 Direction 156 Direction of a pseudoreflection 186 Direction of a transvection 156 Discriminant 5 35 Divided polynomial algebra 178 Dominance ordering 70 Double complex 174 Doubly polarized elementary symmetric polynomials 91 Eagon — Hochster theorem 130 Eilenberg — Moore 174 Eilenberg, S. 121 Elementary matrix 110 Embedding property 242 Embedding theorem 243 272 291 Essential monomorphism 249 Euler characteristic 178 Euler class 104 155 213 230 270 273 Euler's formula 119 127 Exactness of 284 Example 230 Example, 5 75 Example, 149 Example, 219 Example, 50 108 Example, 218 Example, 11 218 219 Example, 217 Example, 82 127 Example, 218 219 Example, 172 Example, 216 Example, 191 Example, 262 Example, 309 Example, 213 218 Example, 309 Example, 213 Example, 309 Example, 309 Example, 215 Example, 309 Example, 215 Example, 309 Example, 213 Example, 276 Example, 23 26 32 39 43 59 133 222 Example, 222 223
Реклама
 |
|
О проекте
|
|
О проекте



![$A[[\xi]]$](/math_tex/4c7aa38680dcd71c0481dca59e2c4cb182.gif)
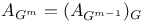
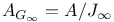
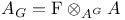
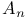
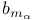
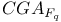
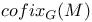
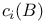
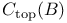
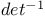 -relative invariant
-relative invariant 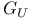
 -module
-module 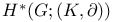
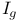
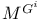
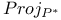
![$Proj_{\mathscr{P}^{*}}(\mathbb{F}_{q}[V])$](/math_tex/9907dac49bfe15c319a98060f63a585682.gif)
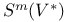
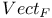
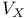
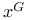
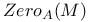
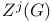
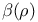
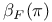
 -relative invariants
-relative invariants 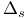
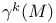
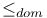
![$\mathbb{F}[-]$](/math_tex/ca82f29590c54b99714a0378218b7c2b82.gif)
![$\mathbb{F}[V]$](/math_tex/9bbba2985617e266a41eefcc59f9cd6b82.gif)
![$\mathbb{F}[V]^{G}$](/math_tex/437f776aae4e524cbb757ec58255f4c282.gif)
![$\mathbb{F}[V]_{G}$](/math_tex/36bd6afabae3783f0f3fbe3236c5aa8c82.gif)
![$\mathbb{F}[V]_{m}$](/math_tex/dc7eff2f89a26d85c45873eaf40e265b82.gif)
![$\mathbb{F}[V]_{\chi}^{G}$](/math_tex/9cb0700c18db61a7e92da6be92c5018d82.gif)
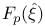
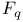
![$\mathbb{F}_{q}[V][[\xi]]$](/math_tex/a8d4aa8059233d0d9b9fc7b72dba212f82.gif)
![$\mathbb{F}_{q}[V]\odot\mathscr{P}^{*}$](/math_tex/045d6ac6977ec8f331378b91f34c74ea82.gif)
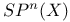
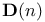
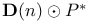
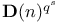
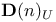
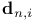
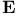
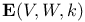
![$\mathbf{E}_{F_{q}[V]\odot\mathscr{P}^{*}}(M)$](/math_tex/9f807eb8313910c959249526287ca82982.gif)
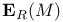
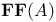
![$\mathbf{J}_{F_{q}[V]\odot\mathscr{P}^{*}}(k)$](/math_tex/d7b866c4a7bd658c9e8e9567a17711ae82.gif)
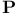
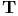
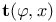
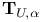
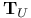
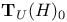
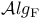
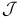 -construction
-construction 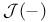
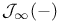

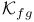
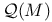
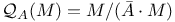
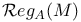
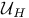
![$\mathcal{U}_{\mathbf{F}_{q}[V]}$](/math_tex/e08bc3809141341ebf216e90b39ba35782.gif)
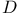
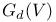
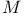
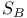
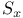
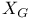
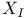
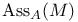
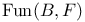
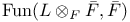
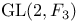
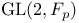
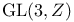
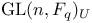
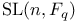
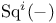
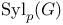
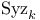
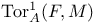
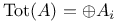
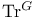
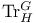
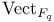
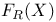
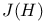
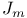
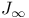
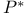
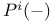
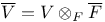
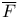
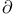
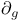
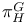
![$\Sigma^{k}(\mathbb{F}_{q}[W])$](/math_tex/0803a2a58df007e5ecb1c9ce3e7ca90482.gif)
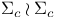
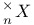
 in
in