јвторизаци€
ѕоиск по указател€м
Wright S. J. Ч Primal-dual interior-point methods
ќбсудите книгу на научном форуме Ќашли опечатку?
Ќазвание: Primal-dual interior-point methodsјвтор: Wright S. J. јннотаци€: In the past decade, primal-dual algorithms have emerged as the most important and useful algorithms from the interior-point class. This book presents the major primal-dual algorithms for linear programming in straightforward terms. A thorough description of the theoretical properties of these methods is given, as are a discussion of practical and computational aspects and a summary of current software. This is an excellent, timely, and well-written work. The major primal-dual algorithms covered in this book are path-following algorithms (short- and long-step, predictor-corrector), potential-reduction algorithms, and infeasible-interior-point algorithms. A unified treatment of superlinear convergence, finite termination, and detection of infeasible problems is presented. Issues relevant to practical implementation are also discussed, including sparse linear algebra and a complete specification of Mehrotra's predictor-corrector algorithm. Also treated are extensions of primal-dual algorithms to more general problems such as monotone complementarity, semidefinite programming, and general convex programming problems.
язык: –убрика: ћатематика /—татус предметного указател€: √отов указатель с номерами страниц ed2k: ed2k stats √од издани€: 1987 оличество страниц: 310ƒобавлена в каталог: 05.11.2010ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
ѕредметный указатель
173 31 54 63 232 247Ч249 56 122 128 130 145Ч146 148 149 152Ч154 204 56 152Ч154 Adjacency graph 214Ч216 Adjacency graph, elimination step for 214Ч215 Affine-scaling algorithm, primal 22 42Ч44 Affine-scaling algorithm, primal-dual 44Ч45 Affine-scaling direction, primal-dual see УNewton step pureФ Algorithm IPF 107Ч125 128 177 180 185 187 190 224 262 Algorithm IPF, complexity of 112 121 Algorithm IPF, convex programming form of 166Ч168 Algorithm IPF, definition of 109Ч110 Algorithm IPF, flexibility in line search 110 125 Algorithm LPF 43 90 96 98 100 102 103 107 108 111 124 128 136 long-stepФ) Algorithm LPF+ 136Ч145 Algorithm LPF+, definition of 138Ч139 Algorithm LPF+, infeasible variant of 154 Algorithm LPF, definition of 96 97 Algorithm MPC 204 206 Algorithm MPC, definition of 195Ч198 Algorithm MPC, ShamanskiiТs algorithm and 199 Algorithm MPC, trajectory following and 201Ч202 Algorithm PC 84 92 93 95 96 102 103 105 128 predictor-corrector Algorithm PC, definition of 93 Algorithm PC, LCP form of 159 160 Algorithm PC, superlinear convergence of 128 135Ч136 145 Algorithm PR 67 68 70Ч72 79 81 Algorithm PR, definition of 67Ч68 Algorithm S3 198Ч199 (see also УShamanskiiТs algorithmФ) Algorithm SPF 84 88 90 91 93 96 102Ч105 short-stepФ) Algorithm SPF, definition of 86 AMPL 258 Analytic center, weighted 42 Armijo condition see УSufficient decrease conditionФ Augmented system form of step equations 16 17 210 220Ч221 227 229 230 235 261 factorizations Barrier function, logarithmic 40 43 Barrier function, logarithmic, defines central path 37 40 Barrier function, logarithmic, for linear program 37 40Ч43 47 Barrier function, logarithmic, KKT conditions for 39 Barrier function, logarithmic, strict convexity of 37 Basic feasible points 33 54 56 Basis 32Ч34 Basis, optimal 33 (see also УVertex solutionФ) Basis, optimal, recovery of 57 150Ч152 225Ч226 Bounds on variables, upper 226Ч228 BPMPD 232 258Ч259 Callable routines 258 Cauchy sequence 144 145 Centering parameter ( 7Ч8 10Ч12 67Ч68 79 83Ч86 91Ч93 95Ч97 104 108 137 158 186 189 193Ч196 198 199 201 205-206 249 Centering parameter ( 14 15 Central path 7Ч9 14 30 43 85 152 153 196 225 Central path, existence of 36Ч40 69 Central path, geometry of 45 154 203 204 Central path, LCP form of 159 Central path, neighborhoods of 9Ч10 83Ч85 90Ч100 129 174 225 Central path, neighborhoods of, 9 19 43 84 85 96Ч105 108 130 133 135 137 144 146 147 155 159 Central path, neighborhoods of, 9 10 43 84Ч92 94Ч98 103Ч105 135 159 Central path, neighborhoods of, 84 Central path, neighborhoods of, infeasible 12 109 111 134 166 186 190 199 203 205 Central path, relationship to KKT conditions 7 36 83 Central path, SDP form of 171 Cholesky factorization, sparse 17 211Ч221 228Ч230 234 235 Cholesky factorization, sparse, dense column handling 17 219 220 233Ч234 259 260 Cholesky factorization, sparse, multiprocessor implementation 212 234Ч235 Cholesky factorization, sparse, small pivot handling 17 216 219 230 232Ч233 Cholesky factorization, sparse, small pivot handling, diagonal pivoting 218 235 236 Cholesky factorization, sparse, small pivot handling, skipping 218Ч219 Cholesky factorization, sparse, stability of 212 216 Combinatorial optimization 14 22 170 Compact set 39 186 Complementarity 4 7 23 158 complexity 21 239 Complexity, algebraic 50 60 Complexity, average-case 50 51 57 Complexity, bit 50 51 60 Complexity, general references for 49 Complexity, interior-point methods and 49 Complexity, polynomial 1 17Ч18 34 44 45 61Ч62 66Ч68 70 77- 80 84 85 87Ч88 90 95Ч97 100 104 108 109 112 114 159 168 185 Complexity, practical performance and 58 Complexity, problem size 51 Complexity, worst-case 50 51 57 Condition number 212 217 247 Conditioning of coefficient matrices 216Ч218 220 Conjugate gradient algorithm, preconditioned 234 260 262 Constraint qualification 165 241 Convex functions 164 168 240 242 250 Convex programming 157 164Ч167 243 250 261 Convex sets 164 167 240 242 Corrector steps 85 92 93 95 105 194Ч197 199 202 203 206 207 Corrector steps, multiple 199 202Ч204 259 260 CPLEX Parallel Barrier 234 CPLEX/Barrier 226 232 259 CPLEX/Simplex 232 CramerТs Rule 53 Crossover to simplex see УBasis optimal recovery Data string see УProblem dataФ Degenerate LCP 173Ч174 Degenerate LCP, no superlinear convergence 174 Degree of a node 213 214 Dense matrices 17 189 Diagonal matrices 16 89 130 131 217 227 246 249 261 DikinТs algorithm see УAffine-scaling algorithm primalФ Divergence of iterates 177 185 188 Dual degenerate linear programs 174 Dual slack variables 3 Dual variables 3 Duality measure ( 7 Duality theory 2Ч4 23Ч29 Efficient algorithms see УPolynomial algorithmsФ Eigenvalues 217 Ellipsoid algorithm 18 49Ч51 53 57 Exponential algorithms 50 FarkasТs lemma 24 34Ч35 45 Fast step 138Ч142 144 Feasible set, dual 23 Feasible set, existence of solutions and 24Ч26 Feasible set, monotone LCP and 159 Feasible set, polygonal form of 33 54 55 57 Feasible set, primal 3 23 33 Feasible set, primal-dual ( 5 9 23 162 185 187Ч188 Fill-in 212Ч213 235 Finite termination 55Ч57 60 62 127 128 146Ч149 154 174 204 225 Finite termination, superlinear convergence and 149 Floating-point arithmetic 57 59 62 Floating-point arithmetic, error analysis of 59 Framework PD 8 11 14 15 18 67 84 86 92 158 170 193 202 Framework PD, LCP form of 158 Free variables 17 221 228Ч230 258 Free variables, splitting of 22 46 163 174 226 228Ч230 Full rank of 31Ч32 37 54 63 155 186 191 211 217 Function long-step 137 139 141 142 GAMS 258 Gaussian elimination 31 Geometric linear complementarity problem 173 Global convergence 12 67 88 111 128 159 Goldman Ч Tucker theorem 21 162 182 241 245 Goldman Ч Tucker theorem, proof of 35Ч36 Goldman Ч Tucker theorem, statement of 28 hessian 240 HoffmanТs lemma 124 148 248Ч249 Homogeneous problem, definition of 180 Homogeneous self-dual (HSD) formulation 107 178 183Ч185 Homogeneous self-dual (HSD) formulation, definition of 183 Homogeneous self-dual (HSD) formulation, detection of infeasibility 185 Homogeneous self-dual (HSD) formulation, implementation of 190 Homogeneous self-dual (HSD) formulation, recovery of primal-dual solution 185 Homogeneous self-dual (HSD) formulation, simplified 174 178Ч183 185 Homogeneous self-dual (HSD) formulation, simplified, detection of infeasibility 182 183 Homogeneous self-dual (HSD) formulation, simplified, implementation of 188Ч190 Homogeneous self-dual (HSD) formulation, simplified, lack of strictly feasibility 181 Homogeneous self-dual (HSD) formulation, simplified, recovery of primal-dual solution 181Ч182 HOPDM 203 232 259Ч260 Horizontal linear complementarity problem (hLCP) 160Ч162 Horizontal linear complementarity problem (hLCP), strict complementarity and 162 Indicators 154Ч155 Infeasible linear programs 2 25Ч26 177 178 181Ч183 Infeasible-interior-point algorithms 2 11Ч12 81 107Ч125 133 178 180 183 188 189 Infeasible-interior-point algorithms, convex programming and 166 Infeasible-interior-point algorithms, finite termination and 146 Infeasible-interior-point algorithms, LCP form of 158 Infeasible-interior-point algorithms, termination test for 186Ч188 Integer programming 22 57 Integer programming, software for 257 Interior Ч Point Methods Online 174 257 Iteration sequence, convergence of 103 144Ч145 162 Iteration sequence, limit points of 100Ч104 108 121 123 127 186 Jacobian 6 13 127 129 164 198 241 KarmarkarТs 18 41 44 65 KarmarkarТs algorithm 1 17Ч18 41 49 53 58 65 KarmarkarТs algorithm, complexity of 18 42 50 62 Karush Kuhn Tucker (KKT) conditions 3Ч5 7 9 13 19 23Ч25 45Ч47 56 83 147 158 161 170 171 175 179 208 226Ч229 236 240Ч241 243 Karush Kuhn Tucker (KKT) conditions, for convex programming 164 Karush Kuhn Tucker (KKT) conditions, for convex quadratic programming 163 Karush Kuhn Tucker (KKT) conditions, sufficiency of 24 47 132 242Ч243 KhachiyanТs algorithm see УEllipsoid algorithmФ Lagrange multipliers 4 241 243 Lagrangian function 165 LAPACK 248 Line search heuristics 80 Linear complementarity problem (LCP), monotone 13 14 43 109 139 154 157Ч162 167 Linear complementarity problem (LCP), monotone, definition of 157Ч158 Linear complementarity problem (LCP), monotone, equivalent formulations of 13 160Ч162 Linear complementarity problem (LCP), monotone, relationship to convex quadratic programming 13 163Ч164 171Ч173 Linear complementarity problem (LCP), monotone, strict complementarity and 162 Linear convergence, Q-linear 111 121 140 252 Linear convergence, R-linear 111 121 253 Linear least-squares problems 17 147 224 250 Linear programming, general references for 21 257 LIPSOL 198 204 219 232 260Ч261 Logarithm, natural 61 68 70 143 245Ч246 LOQO 198 232 261 MehrotraТs predictor-corrector algorithm 2 14Ч16 85 193Ч208 210 234 MehrotraТs predictor-corrector algorithm, motivation for 194Ч195 MehrotraТs predictor-corrector algorithm, superquadratic convergence of 198Ч199 MehrotraТs predictor-corrector algorithm, variants of 204Ч207 Minimum-degree orderings 213Ч216 235 260 262 Minimum-local-fill orderings 215 216 259 261 Mixed monotone linear complementarity problem (mLCP) 160Ч164 174 179 189 191 227 Mixed monotone linear complementarity problem (mLCP), step equations for 161 Mixed monotone linear complementarity problem (mLCP), strictly complementary solutions of 162 179 181 182 244Ч245 MPS input format 258 NEOS Server 257 263 Nested-dissection orderings 216 235 NETLIB 190 207 Network optimization 21 58 234 Network optimization, software for 257 Newton Barrier XPRESS Ч MP 261Ч262 Newton step, pure 6Ч8 12 15 44 127Ч135 137 138 154 174 194Ч197 199 200 202 206 207 249 NewtonТs method 4 6 12 14 41 83 127 136 149 158 165 NewtonТs method, Kantorovich analysis of 127 129 Nonconvex problems 14 Nondegenerate solution 13 199 Nonlinear complementarity problems, monotone 14 43 157 167 Nonlinear equations 6 12 198 Nonnegative orthant 6 11 13 33 Normal equations form of step equations 16Ч17 210 215 220 221 228- 234 259 260 262 sparseФ) Opening the cone 137Ч139 Optimization problems 1 60 239 Optimization problems, constrained 3 4 39 45 104 240 Optimization problems, global solutions of 240 242 Optimization problems, local solutions of 240 242 Optimization problems, unconstrained 149 Order notation 239 Ordinary differential equations 92 199 orthogonal matrices 155 246 247 OSL 262Ч263 Pairwise products 7Ч9 11 36 37 79 84Ч86 89 109 141 196 197 204 205 Partition 27Ч29 32 56 121 128 131 145Ч149 217 Path-following algorithms 2 9Ч10 14 50 107 121 144 174 203 217 Path-following algorithms, complexity of 61Ч62 68 84 95Ч96 100 159 Path-following algorithms, finite termination and 146 Path-following algorithms, homotopy methods and 9 Path-following algorithms, long-step 10 43 85 90 96Ч100 102 103 109 Path-following algorithms, motivation for 83 Path-following algorithms, predictor-corrector (Mizuno Ч Todd-Ye) 10 44 84 91Ч96 102 103 105 Path-following algorithms, relationship to potential-reduction algorithms 78 81 Path-following algorithms, short-step 10 43 84Ч91 102 104 Path-following algorithms, strictly complementary limit points of 181 PCX 198 258 263 Permutation matrices 54 211 212 248 Polynomial algorithms 50 52 57 58 60 63 135 polynomialФ) Positive definite matrices 211 (see also УSemidefinite matricesФ) Positive semidefinite matrices 13 19 Potential function 10 Potential function, Tanabe Ч Todd Ч Ye, quadratic approximation to 70Ч78 Potential function, Tanabe Ч Todd Ч Ye, relationship to 67 69 Potential function, Tanabe Ч Todd Ч Ye, SDP form of 171 Potential function, Tanabe Ч Todd-Ye 11 19 44 65Ч81 Potential-reduction algorithms 2 10Ч44 65Ч81 Potential-reduction algorithms, centrality of iterates 78Ч79 Potential-reduction algorithms, complexity of 70 77Ч80 84 Potential-reduction algorithms, practical variants of 80 Potential-reduction algorithms, pure primal 62 81 Predictor steps 84 92Ч96 105 135 194 Preprocessing see УPresolvingФ Presolving 209 220 230 232 Primal degenerate linear programs 174 Problem data 51 59 60 152 255 Problem data, definition of 51 Problem data, integer 51 54 56 58 63 Problem data, rational 51 Problem data, storage of 51 53 Problem dimension 58 Problem dimension, definition of 51 Procedure FT 55Ч57 128 147 152 154Ч155 Procedure FT, definition of 146Ч147 Procedure OB Ч D 151Ч152 Procedure OB Ч P 151 Q-order of convergence 142 144 154 252 Quadratic convergence 127 252 Quadratic programming, convex 2 13 14 19 131 133 134 157 160 163Ч164 174Ч175 261 Quadratic programming, convex, quadratically constrained 167 170 Quadratic programming, convex, relationship to LCP 13 Rank of matrices 246 249 250 Rank-deficient matrices 211 247 Rational arithmetic 52Ч54 57 59 Rational-number model 49 52 59Ч60 255 Rational-number model, emulated on Turing machine 52 54 Real-number (BSS) model 50 59 60 63 Remaining matrix 213 235 RenegarТs algorithm 41Ч42 44 53 65 Residuals 11 12 109 111 129 134 155 167 185Ч189 191 206 226 229 Roundoff error 59 60 62 217 Roundoff error, unit 212 221 Safe step 138Ч140 142 Schur complement 233 260 Self-concordancy 166 168 Self-dual linear programs 178Ч180 184 191 Self-dual linear programs, mLCP formulation of 180 184 243Ч245 Semidefinite matrices 158 163 174 210 218 240 Semidefinite programming (SDP) 13 157 167Ч171 174 ShamanskiiТs algorithm 193 198Ч199 Sherman Ч Morrison Ч Woodbury formula 189 220 233 236 250Ч251 260 Simplex method 1 32 33 225 232 234 Simplex method, complexity of 17 49 50 57 Simplex method, hot-starting of 225 Simplex method, Klee Ч Minty example 18 57 Simplex method, performance of 17
–еклама
 |
|
ќ проекте
|
|
ќ проекте



 linear complementarity problem
linear complementarity problem 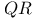 factorization
factorization 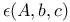
 )
) 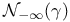

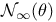
 ), definition of
), definition of  )
)