|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Mirsky L. — An introduction to linear algebra |
|
|
 |
| Предметный указатель |
Abelian groups 254
Adjugate, determinant 24-27
Adjugate, determinant, matrix 88-90
Affine classification of quadrics 381-4
Algebraic complement see Cofactor.
Alternating group 287
Angle of an orthogonal matrix 236
Arrangements 2-5
Augmented matrix 140
Automorphisms of a linoar manifold 125-6 268-9
Axis of rotation 240
Basis, basis theorems 51-53
Basis, change of basis in a linear manifold 111-13
Basis, completion 54
Basis, orthogonal and orthonormal 65-68 155-6
Bilinear, forms 354-6 368-9
Bilinear, operators 353-6
Bilinear, symmetric bilinear operators 361
Biunique correspondence 4
Bondixon’s inequality 210
Bossel’s inequality 70
Bromwich’s inequality 388-9
Canonical form(s), classical 312
Canonical form(s), classical of matrices 290-316
Canonical form(s), classical of quadratic forms 378
Cayley and Hamilton, theorem of 206
Characteristic, equation 195
Characteristic, inequalities for characteristic roots 210-12 309-11 388-90
Characteristic, polynomial 195 197-208
Characteristic, regular characteristic roots 294
Characteristic, roots 195
Characteristic, roots of rational functions of matrices 201-2
Characteristic, vectors 214
Circulant 36
Classical canonical form 312
Classification of quadrics 380-5
Cofactor, of an element 14
Cofactor, of an element of a minor 21
Collineations 123 196 256 380-5
Column, matrix 77
Column, matrix, rank 137
Column, matrix, vector 77
Commuting matrices 81
Complements 64-57
Complements, orthogonal 68-69
Completion of basis 54
Congruence transformations 182-5 266 358-60
Congruent matrices 182
Consistency of systems of linear equations 132 140-1
Convergence, of matrix sequences 327-9
Convergence, of matrix sequences of matrix series 330-2
Cramer’s Rule 134
Critical minor 136
Definite hermitianand quadratic forms 394 398-404
Determinant rank 136
Determinant(s), adjugate 24-27
Determinant(s), axiomatic characterization 189-92
Determinant(s), definition 6
Determinant(s), dominated by diagonal elements 32-33
Determinant(s), expansions by rows and columns 15
Determinant(s), Gram determinant 155
Determinant(s), inequalities 33 212-13 416-22
Determinant(s), multiplication 12-13
Determinant(s), of a matrix 87
Determinant(s), Vandermonde determinant 17-18
Determinantal criteria for value classes 400-7
Diagonal, canonical forms 290-306
Diagonal, matrix 76
Differential, equations 343 8
Differential, operators 126-7 133-4
Differentiation, of determinants 36
Differentiation, of matrices 339
Dimensionality, of a linear manifold 50
Dimensionality, theorem for homogeneous systems 149
Discriminant 18-19
Disposable unknowns 142
Divisors of zero 95-96 153-4
Elementary, divisors 194
Elementary, matrices (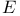 -matrices) 170 -matrices) 170
Elementary, operations (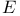 - operations) 168-78 - operations) 168-78
Equivalence, class 187
Equivalence, of bilinear forms 368
Equivalence, of matrices 176
Equivalence, of quadratic forms 376-9
Equivalence, of systems of linear equations 142
Equivalence, relation 186
Equivalence, transformations 177
Equivalence, w.r.t. operators 189 267
Euler, equations of transformation 242
Euler, theorem on rigid motion 246
Exponential function of a matrix 336-41
Field 39
Field, real and complex 40
Finite groups 254 270-1
Fischer’s inequality 420
Forms, bilinear 364-6 368-9
Forms, hermitian 386-8 416
Forms, polarized 362
Forms, quadratic 357-60
Frobenius, determinantal criterion for positive definite forms 400
Frobenius, theorem on non-negative matrices 329
Frobenius, theorem on rank 162
Full linear group 263 268-9
Functions of matrices 336 342-3
Fundamental sets of solutions 151
Generators, of a linear manifold 45
Generators, of a linear manifold of a vector space 43
Gram, determinant and matrix 155
Gram, determinant and matrix, inequality 423
Group(s), Abelian 254
Group(s), alternating 287
Group(s), axioms 252
Group(s), centre 254
Group(s), congruence group 266
Group(s), finite 254 270-1
Group(s), full linear 263 268-9
Group(s), group matrix 273
Group(s), isomorphism 259
Group(s), multiplication table 1
Group(s), of matrices 261-5
Group(s), of permutations 257-8 271-2
Group(s), of singular matrices 272-6
Group(s), order 254
Group(s), orthogonal 263
Group(s), orthogonal similarity group 266
Group(s), projective 263
Group(s), representation by matrices 267-72
Group(s), rotation group 263
Group(s), similarity group 266
Group(s), symmetric 257
Hadamard’s inequality 418-19
Hamilton see Cayley.
Hermitian, forms 386-8 415
Hermitian, matrices 209 301 304
Hermitian, positive definite forms 394 398-404
Hirsch’s inequality 211
Homogeneous linear equations 27-30 131 148-52
Homogeneous linear equations, dimensionality theorem 149
Homogeneous linear equations, fundamental sots of solutions 151
Idempotent matrix 107
Image space 277
Indefinite hermitian and quadratic forms 394 407
Index laws for matrices 83 93-94
Inequality(ies), for characteristic roots 210-12 309-11 388-90
Inequality(ies), for determinants 33 212-13
Inequality(ies), for positive definite matrices 416-22
Inequality(ies), of Bendixon 210
Inequality(ies), of Bessel 70
Inequality(ies), of Bromwich 388-9
Inequality(ies), of Fischer 420
| Inequality(ies), of Gram 423
Inequality(ies), of Hadamard 418-19
Inequality(ies), of Hirsch 211
Inequality(ies), of Minkowski 419-20
Inequality(ies), of Oppenheim 421
Inequality(ies), of Ostrowski 212-13
Inequality(ies), of Schur 309-11 422
Inequality(ies), triangle 64
Inertia, law of, for hermitian forms 387
Inertia, law of, for hermitian forms for quadratic former 377
Infinitesimal rotation 249
Inner product 62
Interpolation formula of Sylvester 221
Invariance 169
Invariant, properties of matrices 122
Invariant, properties of matrices, spaces 277-86
Inverse matrix 91 178-9
Isomorphism, between groups 259
Isomorphism, betweon linear manifolds 68-59 123-4
Jacobi’s theorem 25
Joachimsthal’s equation 360-2
Klein four-group 261
Kronecker delta 20
Lagrango’s method of reduction 371 4
Laplace’s expansion theorem 21
Latent roots see Characteristic roots.
Latent vectors see Characteristic vectors.
Leading element 173 (footnote)
Length of a vector 63
Linear manifold (s), automorphism 6 268-9
Linear manifold (s), basis 49-54
Linear manifold (s), change of basis 111-13
Linear manifold (s), definition 44
Linear manifold (s), dimensionality 50
Linear manifold (s), generators 45
Linear manifold (s), isomorphism 58-59 123-4
Linear manifold (s), of matrices 80
Linear manifold (s), representation by a vector space 60
Linear manifold (s), spanned by given elements 45
Linear manifold (s), zero element 45
Linear, combination of vectors 42
Linear, dependence 48 152-3
Linear, equations 27-30 131-52 180-1
Linear, forms 153
Linear, full linear group 263 268-9
Linear, homogeneous equations 27-30 131 148-52
Linear, operators (operations, transformations) 114-22 277
Linear, substitutions 74 85-87
Linear, transformations of a bilinear form 356
Linear, transformations of a quadratic form 360
Majorization of matrices 328
Mapping 113
Mapping, into 116
Mapping, onto 124
Matrix (matrices), addition 78-79
Matrix (matrices), adjugate 88-90
Matrix (matrices), augmented 140
Matrix (matrices), column type and row type 77
Matrix (matrices), commuting 81
Matrix (matrices), congruent 182
Matrix (matrices), definition 74
Matrix (matrices), determinant of 87
Matrix (matrices), diagonal 76
Matrix (matrices), elementary 170
Matrix (matrices), elementary divisors 194
Matrix (matrices), equations 298-300
Matrix (matrices), equivalence 176
Matrix (matrices), functions 336 342-3
Matrix (matrices), of coefficients 140
Matrix, Gram 156
Matrix, group matrix 273
Matrix, groups 6
Matrix, hermitian 209 301 304
Matrix, idempotent 107
Matrix, index laws 83 93-94
Matrix, invariant properties 122
Matrix, inverse 91 178-9
Matrix, linear manifold of 80
Matrix, multiplication 80-85
Matrix, multiplication by scalars 78
Matrix, normal 305-6 309-10
Matrix, orthogonal 222-9
Matrix, partitioned 100-6
Matrix, periodic 298
Matrix, permutation matrices 271
Matrix, polynomials 97-99 201-8 342-3
Matrix, power series 332-43
Matrix, rank 136-40 158-63
Matrix, rational functions 99-100 201-2 204 5 335
Matrix, representations of groups by matrices 267-72
Matrix, scalar 76
Matrix, sequences 327-9
Matrix, series 330-2
Matrix, similar 119
Matrix, singular and nonsingular 87
Matrix, skew-Hermitian 209 232
Matrix, skew-symmetric 208 227 243-5
Matrix, square 75
Matrix, symmetric 183 209 301-4
Matrix, transposed 76 97
Matrix, triangular 76
Matrix, unit 75
Matrix, unitary 229-32
Matrix, zero 75
Maximal invariant space, of a linear transformation 277-82
Maximal of a group of transformations 282-6
Metric classification of quadrics 385
Minimum polynomial 203-4 207-8 297-8
Minkowski, inequality for positive definite matrices 419-20
Minkowski, theorem on dominated determinants 31-32
Minor, cofactor of 21
Minor, critical 136
Minor, of a determinant 20
Minor, of a matrix 136
Minor, principal 197
Monic polynomial 203
Motion, proper and improper 246
Motion, rigid 246-7
Multiplication table for groups 260-1
Non-commutativity of matrix multiplication 81
Non-negative matrix 328-30
Non-singular matrix 87
Norm of a vector 63
Normal form, reduction of a matrix to 173-6
Normal matrix 305-6 309-10
Normalization of a vector 64
Nullity, Sylvester’s law of 162
Operations, elementary 168-78
Operators, bilinear 353-6
Operators, differential 7 133-4
Operators, linear 114-22 277
Operators, multiplication 172
Operators, polarized 361
Operators, quadratic 357-9 361-2
Oppenheim’s inequality 421
Orthogonal angle 236
orthogonal matrices 222-9
Orthogonal principal vector 237
Orthogonal proper and improper 233
Orthogonal, basis 65-68
Orthogonal, complement 68-69
Orthogonal, congruence group and transformation 266
Orthogonal, group 263
Orthogonal, reduction of quadratic forms 362-3
Orthogonal, reduction of symmetric matrices 4
Orthogonal, set 65-67
Orthogonal, similarity 266
Orthogonal, vectors 64
Orthogonalization process of Schmidt 67-68
Orthonormal bases and sets 65-68 155-6
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



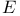 -matrices)
-matrices)