|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| John Strikwerda — Finite difference schemes and partial differential equations |
|
|
 |
| Предметный указатель |
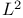 norm on grid 29 39 norm on grid 29 39
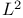 norm on real line 38 norm on real line 38
ADI methods 172—185 342
ADI methods for second-order equations 202
ADI methods with mixed derivatives 181
ADI methods, boundary conditions for 176
ADI methods, implementation of 177—180
ADI methods, stability 177
Admissible solution 291 301
Amplification factor 48
Amplification factor for multistep scheme 97 267
Amplification factor of second-order equations 193 271
Amplification matrix 166
Amplification polynomial 103 123 245 289
Analytic function 419
Artificial viscosity 161
Backward-time backward-space scheme 35
Backward-time central-space scheme for hyperbolic equations 35 57
Backward-time central-space scheme for the heat equation 147
Biharmonic equation 313
Block tridiagonal systems 90
boundary conditions 176
Boundary conditions for ADI schemes 176
Boundary conditions for elliptic equations 322
Boundary conditions for finite difference schemes 85 281
Boundary conditions for parabolic equations 152
Boundary conditions, analysis of 279
Box scheme 57 77
Box scheme, modified 78
Brownian motion 141
Cauchy — Riemann equations 313
Cauchy — Schwarz inequality 377
Cell Peclet number 159
Cell Reynolds number 159
CFL condition 34
Chapman — Kolmogorov equation 141
Characteristics 2
Characteristics for systems 9
Characteristics for variable coefficients 5
Characteristics, incoming 11
Characteristics, outgoing 11
Checkerboard ordering 359
Cholesky factorization 395
Cholesky factorization, preconditioning 395
Conjugate gradient method 377
Conjugate search directions 380
Conjugate transpose 401
Conservative polynomial 109
Consistent scheme 25
Consistently ordered matrix 357
Continuity of the solution on the data 205
Convection-diffusion equation 140 157
Convergence estimate 387
Convergence estimate, implementation 384
Convergence estimates for nonsmooth initial functions 252—258
Convergence estimates for parabolic equations 259—261
Convergence estimates for smooth functions 235—246
Convergent scheme 23 262
Coordinate changes and schemes 335
Courant — Friedrichs — Lewy condition 34
Crank-Nicolson scheme for heat equation 147
Crank-Nicolson scheme for heat equation, nondissippative 151
Crank-Nicolson scheme for hyperbolic, adding dissipation to 123
Crank-Nicolson scheme for hyperbolic, boundary conditions 86 292
Crank-Nicolson scheme for hyperbolic, equations 63
Crank-Nicolson scheme for hyperbolic, modified 85
Crank-Nicolson scheme for hyperbolic, order of accuracy 68
Crank-Nicolson scheme for hyperbolic, solution of 88
Crank-Nicolson scheme for hyperbolic, stability of 77
Diagonalizable matrix 3
Diagonally dominant matrices 349
Difference calculus 78—82
Dirichlet boundary condition 145 152 176 199 311
dispersion 125
Dispersion in higher dimensions 202
Dispersive equation 190
Dissipation 122
Dissipation and smoothness of the solution 149
Dissipation for parabolic schemes 146
Dissipation, adding to nondissipative schemes 123
Dissipation, convergence estimates 259
Douglas — Rachford method 175
Du Fort — Frankel scheme 148 268
Duhamel’s principle 32 225 262
Dynamic stability 59
D’Yakonov scheme 175
Efficiency of higher order schemes 101 181
Eigenvalue of a matrix 403
Eigenvalue of a matrix, semisimple 403
Eigenvector 403
Eigenvector, generalized 403
Elliptic equations, boundary conditions 322
Elliptic equations, differentiability of the solution 314
Elliptic equations, discontinuous boundary data 322
Elliptic equations, regularity estimates 315
Energy method 145 191
Envelope of a wave packet 130
Euler backward scheme 57 75
Euler — Bernoulli equation 190
Euler — Bernoulli equation and piecewise smooth functions 256—258
Euler — Bernoulli equation, evaluation operator 242
Euler — Bernoulli equation, scheme for 195 200
Explicit schemes, definition 34
Exponential of a matrix 214 406
Faber — Krahn inequality 358
Factor space 367
Finite difference grid 16
Finite Fourier transform 46
Five-point (discrete) Laplacian 325
Fokker — Planck equations 140
Forward-time backward-space scheme 17 47
Forward-time central-space scheme 17
Forward-time central-space scheme and smoothing 55
Forward-time central-space scheme for hyperbolic equations 17 51
Forward-time central-space scheme for the heat equation 145
Forward-time forward-space scheme 17 27
Fourier analysis on the integers Z 38
Fourier analysis on the real line 37
Fourier analysis, differentiability of functions 42
Fourier inversion formula on the grid 38
Fourier inversion formula on the integers 38
Fourier inversion formula on the real line 37
Fourier inversion formula, multidimensional 44
Fourier series 38
Fourier transform in higher dimensions 44
Fourier transform of derivatives 42
Fourier transform on the integers 38
Fourier transform on the real line 37
Fourth-order accurate approximations of first derivative 79 80
Fourth-order accurate approximations of second derivative 80
Fourth-order accurate nine-point Laplacian 328
Frozen coefficient problems 59 276
Function spaces, 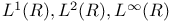 417 417
Gauss — Seidel algorithm 340
Gauss — Seidel algorithm and diagonally dominate matrices 349—351
Gauss — Seidel algorithm, analysis of 347
Gauss — Seidel algorithm, iteration matrix for 345
Gaussian elimination 88 89 339
Gaussian elimination, grid 16
Group velocity 130 190 248
Gustaffson-Kreiss-Sundstrom-Osher (GKSO) method 288 309
Harmonic functions 311 319 419
Heat equation 137
Hermitian matrix 226 230 408
Hurwitz polynomial 117
Hyperbolic equation 1
Hyperbolic equation with variable coefficients 5
Hyperbolic equation, differentiability of solutions 2
Hyperbolic systems 3 166 217
Hyperbolic systems, weakly 221
| Implementation of iterative methods 346
Implicit schemes 34
Implicit schemes, solution of 88
Initial value problem for heat equation 137
Initial value problem for one-way wave equation 1
Initial value problem for second-ordcr equations 187
Initial value problem, analysis of 205—225
Initial-boundary value problems 275—310
Initial-boundary value problems for hyperbolic schemes 291
Initial-boundary value problems for parabolic schemes 292
Initial-boundary value problems for partial differential equations 300
Initialization for leapfrog scheme 18
Initialization of multistep schemes 18 98 269
Initialization of schemes for second-order equations 197
Integrability condition 312 370
Interior regularity estimate for finite difference schemes 330
Interior regularity estimate for partial differential equations 315
Interpolation operator 236
Irreducible matrix 349
Iteration matrix 341
Iteration matrix for 345
Jacobi method 340
Jacobi method for diagonally dominate matrices 349
Jacobi method, analysis of 345 346
Kreiss matrix theorem 225—233
Laplacc’s equation 311
Laplace transform 276 291
Laplace transform of a discrete function 277
Laplacian operator 311
Lax — Friedrichs scheme 17
Lax — Friedrichs scheme, stability 51
Lax — Richtmyer equivalence theorem 32—33
Lax — Richtmyer equivalence theorem for second-order equations 194
Lax — Richtmyer equivalence theorem, proof 262—266
Lax — Wendroff schcme 61 70
Lax — Wendroff schcme for parabolic equations 162
Lax — Wendroff schcme, dispersion 126
Lax — Wendroff schcme, dissipation 122
Lax — Wendroff schcme, modified 84
Lax — Wendroff schcme, smallest stencil 72
Lax — Wendroff schcme, stability of 76
Lcbesgue dominated convergence theorem 264 416
Leapfrog scheme for adding dissipation to 123
Leapfrog scheme for dispersion of 127
Leapfrog scheme for heat equation 147
Leapfrog scheme for hyperbolic equations 17 195 267
Leapfrog scheme for hyperbolic equations, explicit 100
Leapfrog scheme for hyperbolic equations, implicit 101
Leapfrog scheme for initialization 98
Leapfrog scheme for parasitic mode 99
Leapfrog scheme for stability of 95—97
Lebesgue integration 415
Lebesgue measure 414
Lexicographic order 340
Line Jacobi method 359
Linear iterative methods 341
Lower order terms and stability 53 149
Lower order terms and well-posedness of systems 218
MacCormack scheme 77
MacCormack scheme, time split 171
Mairix method for analyzing stability 307
Matrix norms 400
Matrix norms, formulas for 404
Maximum principle for analytic functions 422
Maximum principle for elliptic equations 317
Maximum principle for the discrete five-point Laplacian 326
Measurable function 414
Measurable set 414
Mitchell — Fairweather scheme 180
Monotone schemes 73
Multistep schemes 18 30 95
Multistep schemes as systems 167
Multistep schemes, convergence 24 267—269
Multistep schemes, dispersion of 127
Multistep schemes, initialization and order of accuracy 269
Neumann boundary condition 145 152 199 312 365—370
Norms for discrete functions 29
Norms for vectors 399
Norms in the factor space 367
Numerical boundary condition 85 281—288
One-way wave equation 1
Order of accuracy and initialization of multistep schemes 269
Order of accuracy and smoothness of parabolic equations 149
Order of accuracy for homogeneous equations 69
Order of accuracy for multistep schemes 267
Order of accuracy of a scheme 64
Order of accuracy of the solution 73
Order of accuracy, lower-order terms and stability of 149
Order of accuracy, parabolic equations 137
Order of accuracy, schemes for 145
Order of accuracy, using symbols 66
Parabolic systems 143 216
Parasitic mode 99
Parasitic mode, dispersion 128
Parseval’s relations 39
Peaceman — Rachford algorithm 175 181
Periodic problems 14
Periodic tridiagonal systems 91
Phase error 126 203
Phase error for multistep schemes 127
Poisson summation formula 250
Poisson’s equation 311
Polar coordinates 333
Positive definite matrix for elliptic schemes 336
Positive definite, iterative method for 362
Preconditioned conjugate gradient method 390
Quasi-characteristic extrapolation 86 282 292 294
Rayleigh equation 191 200
Reducible matrix 349
Reentrant corners 324 331
Regularity estimates 314 315 330
Residual 374
Resolvent condition for finite difference equations 227 289
Resolvent condition for partial differential equations 301
Restricted stability condition 50
Reverse Lax — Friedrichs scheme 36 58
Riemann integral 416
Robin condition 322
Robustness 206
Rouchfi’s theorem 110
Scalar product 401
SchrOdinger equation. 191
Schur polynomial 108 109 125 198
Schur’s lemma 403
Schwartz class 46
Search direction 378
Second-order equations 187
Second-order equations, convergence estimates for 270
Semi simple eigenvalue 404
Sherman — Morrison formula 91
Simple root 104
Simultaneously diagonalizable 169
SOR 340
SOR and Neumann boundary condition 368
SOR, analysis of 351
SOR, efficiency of 356
SOR, estimating the parameter 358
SOR, implementation 360
SOR, line 359
Spectral radius 341 404
SSOR 359 391
SSOR, preconditioner 391
Stability and lower-order terms 53
Stability and variable coefficients 59
Stability and von Neumann polynomial 108
Stability for ADI methods 177
Stability for ADI methods, condition, general 50
Stability for ADI methods, definition 28
Stability for initial-boundary value problems 288
Stability for multistep schemes 105
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



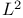 norm on grid
norm on grid