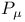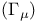јвторизаци€
ѕоиск по указател€м
Weinberg S. Ч The Quantum Theory of Fields. Vol. 1 Foundations
ќбсудите книгу на научном форуме Ќашли опечатку?
Ќазвание: The Quantum Theory of Fields. Vol. 1 Foundationsјвтор: Weinberg S. јннотаци€: In The Quantum Theory of Fields, Nobel Laureate Steven Weinberg combines his exceptional physical insight with his gift for clear exposition to provide a self-contained, comprehensive, and up-to-date introduction to quantum field theory.
язык: –убрика: ‘изика / вантова€ теори€ пол€ /”чебники /—татус предметного указател€: √отов указатель с номерами страниц ed2k: ed2k stats √од издани€: 1996 оличество страниц: 609ƒобавлена в каталог: 09.10.2005ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
ѕредметный указатель
Quarks 217 531 Rabi, I. I. 36 48 Racah, G. 45 Radiative corrections (see УRenormalizationФ УQuantum УUltraviolet УInfrared УSelf-energy УVertex УVacuum УSoft Ramsauer 165 Ramsauer Ч Townsend effect 165 Rarita Ч Schwinger field 232 423 Rarita, W. 232 257 Rates, general formuia 134 Rays, defined 49Ч50 Rechenberg, H. 45 Reduction formula 436Ч8 Redundant couplings 331Ч2 522Ч3 Regge trajectories 468Ч9 Regge, T. 468 469 477 Relativistic wave equations 1Ч14 Relevant couplings 530 Renormalizability 37 499 502Ч3 516Ч25 Renormalization 34Ч8 506Ч16 УField УMass Renormalization group 490 516 525 Representations of groups, defined 53 Representations of homogeneous Lorentz group 229Ч33 Resonances 159Ч65 Retherford, R. C. 47 Richardson O. 47 Riemann Ч Lebesgue theorem 181 Roberts, J. E. 424 Robertson, P. P. 42 Rochester, G. D. 30 45 123 767 Rohrlich, F. 257 Rose, M. E. 46 106 167 168 257 596 Rosenbluth formula 457 Rosenbluth, M. N. 457 470 Rosenfeld, L. 19 44 198 256 338 Rotation matrices 68 Rueger, S. M. 424 Rydberg unit (Ry), defined 593 S-matrix 4 33 S-matrix, C, CP and CPT 131Ч4 S-matrix, defined 113 S-matrix, internal symmetries 121Ч4 S-matrix, Lorentz invariance 116Ч21 S-matrix, parity 124Ч7 S-matrix, PT 130Ч1 133 S-matrix, S-Operator 114 S-matrix, time reversal 127Ч30 S-matrix, unitarity 113Ч14 147Ч51 УM-matrixФ) Sakata, S. 45 532 Sal peter, E. E. 560 563 Salam, A. 39 42 512 532 Sapirstein, J. R. 596 Scattering amplitude (f) 148 153Ч4 466Ч7 Scattering lengths, defined 157 Schaefer, G. W. 596 Schearer, J. F. 47 Schiff, L. I. 41 43 168 563 596 Schmidt-Kaler, F. 596 Schrader, R. 424 Schroedinger picture 109 Schroedinger, E. 3 4 6 13 27 47 109 Schroer, B. 257 Schubert, K. R. 767 Schur, I. 257 Schwarz, J. H. 375 Schweber, S. S. 39 40 Schwinger action principle 288 Schwinger terms 449 Schwinger, J. 14 33 35 36 37 38 40 43 46 47 48 111 766 232 257 259 291 375 376 424 470 489 498 Screaton, R. 477 Second class constraints (see УConstraints secondary constraintsФ УConstraintsФ) Seiler, R. 257 Self-energy functions 439 473Ч80 493Ч6 508Ч9 512Ч15 575Ч9 583Ч4 Semi-simple Lie groups and algebras, defined 70 86 Sen, S. 106 Separable interactions 165 Serber, R. 46 48 Shelter Island Conference (1947) 34Ч8 Shifman, M. A. 555 Simply connected spaces, defined 84 SL(2, C) group 87 90 Slater, J, C. 42 Soft photons 534Ч48 553Ч6 Sommerfield, A. 3 5 6 11 47 Spaarnay, M. J. 338 Space inversion (see УParity and space inversionФ) Spectral functions (see УKaellen-Lehmann representationФ) Spherical harmonies 153 569 Spin matrices, defined 230 Spin sums 210 224 236Ч7 252 360Ч1 365 545 Spin(d) group 90 Spin-statistics connection 238 Spontaneous emission of photons 17Ч19 590 Stachel, J. 44 256 Standing wave states 166 Steinberger, J. 167 Sterman, G. 563 Stevenson, E. C. 30 Stoner, E. C. 42 Stora, R. 39 Strangeness and strange particles 123 (see УK mesonsФ УHyperonsФ) Stratonovich, R. L. 461 470 Streater, R. F. 257 258 Street, J. C. 30 String theory 1 15 244 371 525 Strong interactions 30 Structure constants, defined 54 SU(2) group 88 123 130 SU(3) symmetry 123 Subtractions in dispersion relations 460 465 Superficial divergences 500Ч2 510 Superrenormalizable interactions 503 507 Superselection rules 53 90Ч1 Supersymmetry 325 506 526 Suura, H. 498 562 Swieca, J. A. 257 Symanzik, K. 438 464 470 Symmetries 50Ч5 91Ч6 306Ч14 425 УGroupsФ УLorentz УParityФ УCharge УTime УInternal УIsospinФ УSU(3)Ф) T-matrix 111 116 141Ч2 152 549 Takahashi, Y. 447 470 Tamm, L. 12 43 44 375 Tate, J. E. 424 Tatti, T. 48 Telegdi, V. L. 106 167 Temporal gauge 346 Thirring, W. 463 477 Thomas, L. H. 42 189 Thomson scattering 369 556 Thomson, J. J. 369 Threshold behavior 157-8 Time reversal (T) consequences for S-matrix 127Ч30 Time reversal (T), defined 58 Time reversal (T), non-conservation 134 Time reversal (T), transformation of 74Ч6 Time reversal (T), transformation of creation operators 177 Time reversal (T), transformation of degenerate multi-plets 100Ч4 Time reversal (T), transformation of Dirac fields 227Ч8 Time reversal (T), transformation of general irreducible fields 242Ч3 Time reversal (T), transformation of one-particle states 77-81 Time reversal (T), transformation of scalar fields 206 Time reversal (T), transformation of vector fields 213 Time-ordered products, defined 143 280 Titchmarsh, E. C. 190 Toll, J. S. 477 Tomonga, S.-I. 36 37 38 40 46 47 48 259 376 Topology of Lorentz and rotation groups 86Ч90 (see also УHomotopy groupsФ УSimply Уde Townsend 165 Traces (see УDirac matricesФ) Tree graphs, defined 283 Tung, W.-K. 106 Turlay, R. 106 167 Turnbull, H. W. 106 Tuve, M. A. 167 Two-cocycles, defined 82 Uehling effect 34 484 581 Uehling, E. A. 34 46 47 484 498 Uhlenbeck, G. E. 5 41 Ultraviolet divergences 31Ч8 476Ч7 482-3 485 491 494Ч7 500Ч5 Umezawa, H. 532 Unitarity gauge 346 Unitarity of S-matrix 113Ч16 129 147Ч51 155 161 521 Universal covering group 90 Vacuum energy 24 26 Vacuum polarization 32 34 473Ч85 581 Vacuum state 24 27 176 Vainshtein, A. I. 533 Van der Waerden, B. 1 40 43 257 Vaughn, M. J. 470 Velo, G. 257 Veltman, M. 477 498 Vertex function 446 485Ч8 507Ч8 579Ч80 Villars, F. 494 498 Waller, I. 31 45 Ward and Ward Ч Takahashi identities 445Ч8 476 508 511 Ward, J. C. 447 470 Watson's theorem 130 Watson, K. M. 130 166 167 Wave packets 109Ч10 Webb, N. 45 Weinberg, S. 40 42 47 105 167 168 190 256 257 338 375 424 470 471 532 533 563 Weinrich, M. 106 167 Weisskopf, V. F. 24 26 28 31 32 34 35 37 40 43 44 45 46 47 593 596 Weitz, M. 596 Wentzel, G. 40 42 46 Wess, J. 338 532 West, T. 375 Weyl, H. 12 43. Wheeler, J. A. 4 33 46 47 166 Whittaker, E. 40 Wichmann, E. H. 189 256 498 Wick rotation 475Ч6 Wick's theorem 261 Wick, G. C. 105 291 475 486 497 498 Wightman, A. S. 105 257 258 Wigner rotation 68Ч73 Wigner three-j symbols 237 Wigner Ч Eckart theorem 153 Wigner, E. P. 19 39 42 43 44 51 62 68 91 93 100 103 104 105 106 108 153 156 162 168 236 Wilczek, F. 424 Williams, E. J. 563 Williams, R. C. 47 Williams, W. E. 47 Wilson's renormalization method 525Ч8 Wilson, W. 41 525 528 533 Witten, E. 40 257 375 Wu, C. S. 106 127 167 Yang, C. N. 106 127 132 167 168 178 189 228 257 375 Yang. C R. 168 Yennie, D. R. 562 596 Yukawa, H. 30 45 159 436 470 Zacharias, J. R. 48 Zakharov, V. I. 533 Zimmerman, W. 438 463 470 512 532 Zumino, B. 257 Zwanziger, D. 257 СInТ and СoutТ states 107Ч12 116 Тt Hooft, G. 377 477 424 498
–еклама
 |
|
ќ проекте
|
|
ќ проекте



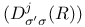

 and
and