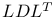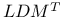|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Golub G.H., van Loan C.F. Ч Matrix Computations |

ќбсудите книгу на
Ќашли опечатку?
¬ыделите ее мышкой и нажмите Ctrl+Enter
|
Ќазвание: Matrix Computations
јвторы: Golub G.H., van Loan C.F.
јннотаци€:
This third edition offers expanded treatment of areas such as CS decomposition, floating point arithmetic, special linear systems, the unsymmetric Lanczos process, and Toeplitz matrix eigenproblems. Other changes to this edition include some 300 new references and 100 new problems, replacement of LINPACK and EISPACK citations with pointers to LAPACK with key codes tabulated at the beginning of appropriate chapters, and correction of the large number of typographical errors in the previous edition. Copyright © 1999 Book News, Inc., Portland, OR All rights reserved Ч This text refers to an out of print or unavailable edition of this title.
язык: 
–убрика: ћатематика/„исленные методы/„исленна€ линейна€ алгебра/
—татус предметного указател€: √отов указатель с номерами страниц
ed2k:
»здание: third edition
√од издани€: 1996
оличество страниц: 694
ƒобавлена в каталог: 21.02.2005
ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
|
|
 |
| ѕредметный указатель |
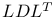 138 138
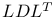 , conjugate gradients and 491Ч493 , conjugate gradients and 491Ч493
A-conjugate 522Ч523
A-norm 530
AasenТs method 163Ч170
Absolute Value notation 62
Accumulated inner product 64
Algebraic multiplicity 316
Angles between subspaces 603
Approximation of a matrix function 562Ч570
Arnoldi factorization 500
Arnoldi method 499Ч503
Back-substitution 89Ч90 153
Backward error analysis 65Ч67
Backward successive over-relaxation 516
Balancing 360
Band algorithms, Cholesky 155Ч156
Band algorithms, Gaussian elimination 152Ч3
Band algorithms, Hessenberg LU 154Ч155
Band algorithms, triangular systems 153
Bandedness 16Ч17
Bandedness, data structures and 19Ч20 158Ч159
Bandedness, lower and upper 16
Bandedness, LU factorization and 152Ч153
Bandedness, pivoting and 154
Bandedness, profile 159
Bandwidth 16
Barrier 287
Bartels Ч Stewart algorithm 367
Basic solution in least squares 258Ч259
Basis 49
Basis, eigenvector 316
Basis, orthonormal 69
Bauer Ч Fike theorem 321
Biconjugate gradient method 550Ч551
Bidiagonal matrix 17
Bidiagonalization upper triangularizlng first 252Ч253
Bidiagonalization, Householder 251Ч253
Bidiagonalization, Lanczos 495Ч496
Big-Oh notation 13
Binary powering 569
Bisection 439
Bit reversal 190
Block algorithms, Cholesky 145Ч146
Block algorithms, cyclic reduction 177Ч180
Block algorithms, data re-use and 43
Block algorithms, diagonalization 366
Block algorithms, Gaussian elimination 116Ч117
Block algorithms, Jacobi 435
Block algorithms, Lanczos 485 505
Block algorithms, LU 101Ч102
Block algorithms, LU with pivoting 116Ч117
Block algorithms, matrix functions and 560Ч561
Block algorithms, QR factorization 213Ч214
Block algorithms, tridiagonal 174
Block algorithms, unsymmetric Lanczos 505
Block Householder 225
Block matrices 24ff
Block matrices, data re-use and 43Ч45
Block matrices, diagonal dominance of 175
Block Schur and matrix functions 560
Block vs.band 176
Bunch Ч Kaufman algorithm 169
Cache 41
Cancellation 61
Cauchy Ч Schwartz inequality 53
Cayley transform 73
CGNE 546
CGNR 545
Characteristic polynomial 310
Characteristic polynomial, generalized eigenproblem and 375Ч376
Chebyshev polynomials 475
Chebyshev semi-iterative method 514Ч516
Cholesky reduction of 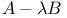 463Ч464 463Ч464
Cholesky, band 155Ч156
Cholesky, block 145Ч146
Cholesky, downdating and 611
Cholesky, gaxpy 143Ч144
Cholesky, outer product 144Ч145
Cholesky, ring 300Ч303
Cholesky, shared memory 303Ч304
Cholesky, stability 146
Chordal metric 378
Circulant systems 201Ч202
Classical Gram Ч Schmidt 230Ч231
Classical Jacobi iteration for eigenvalues 428Ч429
Colon notation 7 19
Column, deletion or addition in QR 608Ч610
Column, partitioning 6
Column, pivoting 248Ч250
Column, weighting in LS 264Ч265
Communication costs 277 280Ч281 287
Companion matrix 348
Complete, orthogonal decomposition 250Ч251
Complete, rank deficiency and 256
Complete, reorthogonalization 482Ч483
Complex, matrices 14
Complex, QR factorization 233
Computation tree 446
Computation/communication ratio 281
Condition number, estimation 128Ч130
Condition of eigenvalues 323Ч324
Condition of invariant subspaces 325
Condition of least squares problem 242Ч245
Condition of linear systems 80Ч82
Condition of multiple eigenvalues 324
Condition of rectangular matrix 230
Condition of similarity transformation 317
Confluent Vandermonde matrix 188
Conformal partition 25
Conjugate gradient method, derivation and properties 490Ч493 520Ч528
Conjugate gradient method, Lanczos and 528
Conjugate, directions 522Ч523
Conjugate, residual method 547Ч548
Conjugate, transpose 14
Consistent norms 55
Constrained least squares 580ff
Contour integral and f(A) 556
Convergence of bisection method 439
Convergence of Chebyshev semi-iterative method 515
Convergence of conjugate gradient algorithm 530
Convergence of cyclic Jacobi algorithm 430
Convergence of Gauss Ч Seidel iteration 511Ч512
Convergence of inverse iteration 408
Convergence of iterative methods 511
Convergence of Jacobi iteration 511Ч512
Convergence of JacobiТs method for the symmetric eigenproblem 429
Convergence of Lanczos method 425Ч427
Convergence of orthogonal iteration, symmetric case 411
Convergence of power method (symmetric) 406Ч407
Convergence of QR algorithm 360
Convergence of QZ algorithm 386
Convergence of Rayleigh Quotient iteration 408Ч409
Convergence of steepest descent 520Ч521
Convergence of SVD algorithm 456
Convergence of symmetric QR iteration 421
Convergence of unsymmetric case 333 336Ч339
Cosine of a matrix 567
Courant Ч Fischer minimax theorem 394
Crawford number 463
Critical section 289
Cross-validation 584
Crout Ч Doolittle 104
CS decomposition 77Ч79
Cyclic Jacobi method 430
Cyclic reduction 177Ч180
Data re-use 34 41
Data structures, block 45
Data structures, diagonal 21Ч22
Data structures, distributed 278
| Data structures, symmetric 20Ч22
Deadlock 280
Decomposition, 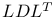 138 138
Decomposition, 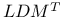 136 136
Decomposition, Arnoldi 500
Decomposition, bidiagonal 251
Decomposition, block diagonal 315
Decomposition, Cholesky 143
Decomposition, companion matrix 348
Decomposition, complete orthogonal 250Ч251
Decomposition, CS (general) 78
Decomposition, CS (thin) 78
Decomposition, generalized real Schur 377
Decomposition, generalized Schur 377
Decomposition, Hessenberg 344
Decomposition, Hessenberg-triangular 378Ч380
Decomposition, Jordan 317
Decomposition, LQ 494
Decomposition, LU 97Ч98
Decomposition, PA=LU 113
Decomposition, QR 223
Decomposition, real Schur 341Ч342
Decomposition, Schur 313
Decomposition, singular value 70
Decomposition, singular value (thin) 72
Decomposition, Symmetric Schur 393
Decomposition, tridiagonal 414
Defective eigenvalue 316
Deflating subspace 381 386
Deflation and bidiagonal form 454
Deflation and Hessenberg-triangular form 381Ч382
Deflation and QR algorithm 352
Departure from normality 314
Derogatory matrix 349
Determinant 50Ч51 310
Determinant and singularity 82
Determinant, Gaussian elimination and 97
Determinant, Vandermonde matrix 191
Diagonal dominance 120
Diagonal dominance, block 175Ч176
Diagonal form 316
Diagonal pivoting method 168Ч169
Differentiation of factorizations 51 103 243 273 323
DIMENSION 49
Distance between subspaces 76Ч77
Distributed memory model 276Ч277
Divide and conquer algorithms, cyclic reduction 177Ч180
Divide and conquer algorithms, Strassen 31Ч33
Divide and conquer algorithms, tridiagonal eigenvalue 444Ч447
Domain decomposition 538Ч539
Dominant, eigenvalue 331
Dominant, eigenvector 331
Dominant, invariant subspace 333
Doolittle reduction 104
Dot product 5
Dot product roundoff 62
DOUBLE PRECISION 64
Doubling formulae 567
DurbinТs algorithm 195
Dynamically scheduled algorithms 288
Efficiency 281
Eigen problem, constrained 621
Eigen problem, diagonal plus rank-1 442
Eigen problem, generalized 375ff 461ff
Eigen problem, inverse 622Ч623
Eigen problem, orthogonal matrix 625Ч631
Eigen problem, symmetric 391ff
Eigen problem, Toeplitz 623Ч625
Eigen problem, unsymmetric 308ff
Eigenvalues, characteristic polynomial and 310
Eigenvalues, computing selected 440Ч441
Eigenvalues, defective 316
Eigenvalues, determinant and 310
Eigenvalues, dominant 331
Eigenvalues, generalized 375
Eigenvalues, interior 478
Eigenvalues, ordering In Schur form 365Ч366
Eigenvalues, sensitivity of (symmetric) 395Ч397
Eigenvalues, sensitivity of (unsymmetric) 320Ч324
Eigenvalues, simple 316
Eigenvalues, singular values and 318
Eigenvalues, Sturm sequence and 440Ч442
Eigenvalues, trace 310
Eigenvector, dominant 331
Eigenvector, left 311
Eigenvector, matrix and condition 323Ч324
Eigenvector, perturbation 326Ч327
Eigenvector, right 311
EISPACK xiv
Elementary Hermitian matrices see УHouseholder matrixФ
Elementary transformations see УGauss transformationsФ
Equality constained least squares 585Ч587
Equilibration 125
Equilibrium systems 170Ч171
Equivalence of norms 53
Error estimation in power method 332
Error, absolute 53
Error, matrix function 563Ч564 566Ч567
Error, relative 53
Error, roundoff 61
Euclidean matrix norm see УFrobenlus matrix normФ
Exchange matrix 193
Exponent range 60
Exponential of matrix 572ff
F-norm 55
Factorization see УDecompositionФ
Fast Fourier Transform 188Ч191
Fast Givens QR 218 228 241
fl 61
Floating point numbers 59
FLOP 18Ч19
Forward error analysis 65Ч66
Forward substitution 88 90 153
Francis QR Step 356Ч358
Frechet derivative 81
Frobenius matrix norm 55
Function of triangular matrix 558Ч561
Gauss transformations 95Ч96
Gauss transformations, Hessenberg form and 349
Gauss-Jordan transformations 103
Gauss-Seidel 510 512Ч513
Gauss-Seidel iteration, solving Poisson equation and 512Ч513
Gauss-Seidel iteration, use as preconditioner 540
Gaussian elimination 94ff
Gaussian elimination, accuracy and 123ff
Gaussian elimination, block version 101
Gaussian elimination, complete pivoting and 118
Gaussian elimination, gaxpy version 100
Gaussian elimination, outer product version 98
Gaussian elimination, partial pivoting and 110Ч113
Gaussian elimination, roundoff error and 104ff
Gaxpy algorithms, band Cholesky 156
Gaxpy algorithms, Cholesky 144
Gaxpy algorithms, Gaussian elimination 114Ч115
Gaxpy in distributed memory 279
Gaxpy in shared memory 286
Gaxpy vs. Outer Product 42
Generalized eigenproblem 375ff 461ff
Generalized least squares 266Ч267
Generalized Schur decomposition 377
Generalized singular value and constrained least squares 580Ч582
Generalized singular value, decomposition 465Ч467
Generalized singular value, proof of 466
Geometric multiplicity 316
Gershgorin circle theorem 320 395
Ghost eigenvalues 484Ч485
givens 216
Givens QR 226Ч227
Givens rotations 215Ч218
Global variables 285
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте