|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Golub G.H., van Loan C.F. Ч Matrix Computations |

ќбсудите книгу на
Ќашли опечатку?
¬ыделите ее мышкой и нажмите Ctrl+Enter
|
Ќазвание: Matrix Computations
јвторы: Golub G.H., van Loan C.F.
јннотаци€:
This third edition offers expanded treatment of areas such as CS decomposition, floating point arithmetic, special linear systems, the unsymmetric Lanczos process, and Toeplitz matrix eigenproblems. Other changes to this edition include some 300 new references and 100 new problems, replacement of LINPACK and EISPACK citations with pointers to LAPACK with key codes tabulated at the beginning of appropriate chapters, and correction of the large number of typographical errors in the previous edition. Copyright © 1999 Book News, Inc., Portland, OR All rights reserved Ч This text refers to an out of print or unavailable edition of this title.
язык: 
–убрика: ћатематика/„исленные методы/„исленна€ линейна€ алгебра/
—татус предметного указател€: √отов указатель с номерами страниц
ed2k:
»здание: third edition
√од издани€: 1996
оличество страниц: 694
ƒобавлена в каталог: 21.02.2005
ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
|
|
 |
| ѕредметный указатель |
gmres 548Ч550
Golub Ч Kahan SVD step 454Ч455
Gram Ч Schmidt, classical 230Ч231
Gram Ч Schmidt, modified 231Ч232
Granularity 284
Growth and Fast Givens transformations 220Ч221 229
Growth and Gauss reduction to Hessenberg form 349Ч350
Growth and Gaussian elimination 111 116
Hessenberg form 344Ч350
Hessenberg form, Arnoldi process and 499Ч500
Hessenberg form, Gauss reduction to 349
Hessenberg form, Householder reduction to 344Ч346
Hessenberg form, inverse iteration and 363Ч364
Hessenberg form, properties 346Ч348
Hessenberg form, QR factorization and 227
Hessenberg form, QR iteration and 342
Hessenberg form, unreduced 346
Hessenberg systems, LU and 154Ч155
Hessenberg-Triangular form, reduction to 378Ч380
Hierarchical memory 41
Holder inequality 153
Horner algorithm 568Ч569
House 210
Householder bidiagonalization 251Ч253
Householder matrix 209Ч215
Hyperbolic transformations 611Ч613
Hypercube 276
Identity matrix 50
Ill-conditioned matrix 82
Im 14
Implicit Q theorem 346Ч347 416Ч417
Implicit symmetric QR step with Wilkinson Shift 420
Implicitly restarted Arnoldi method 501Ч503
Incomplete block preconditioned 536Ч537
Incomplete Cholesky 535
Incurable breakdown 505
Indefinite systems 161ff
Independence 49
Inertia of symmetric matrix 403
Inner product, accumulation of 64
Inner product, roundoff error and 62Ч64
Integrating f(A) 569Ч570
Interchanges see УPivotingФ
Interlacing property 396
Intersection of subspaces 604Ч605
Invariant subspace 372 397Ч403
Invariant subspace, approximate 400Ч403
Invariant subspace, dominant 333
Invariant subspace, perturbation of 324Ч326 397Ч400
Invariant subspace, Schur vectors and 313
Inverse eigenvalue problems 622Ч623
Inverse error analysis see УBackward error analysisФ
Inverse iteration 362Ч364 408
Inverse iteration, generalized eigenproblem 386
Inverse of matrix 50
Inverse of matrix, computation of 121
Inverse of matrix, perturbation of 58Ч59
Inverse of matrix, Toeplitz case 197
Inverse orthogonal iteration 339
Iteration matrix 512
Iterative improvement for least squares 267Ч268
Iterative improvement for linear systems 126Ч128
Iterative methods 508ff
Jacobi iteration for symmetric, cyclic 430
Jacobi iteration for symmetric, eigenproblem 426
Jacobi iteration for symmetric, parallel version 431Ч434
Jacobi iteration for the SVD 457
Jacobi method for linear systems, preconditioning with 540
Jacobi rotations 426 (See also УGivens rotationsФ)
Jordan blocks 317
Jordan decomposition 317
Jordan decomposition, computation 370Ч371
Jordan decomposition, matrix functions and 557 563
Kaniel Ч Paige theory 475Ч477
Krylov subspace methods, biconjugate gradients 550Ч551
Krylov subspace methods, CGNE 546
Krylov subspace methods, CGNR 545
Krylov subspace methods, conjugate gradients 490ff 520ff
Krylov subspace methods, GMRES 548Ч550
Krylov subspace methods, MINRES 494
Krylov subspace methods, QMR 551
Krylov subspace methods, SYMMLQ 494
Krylov, matrix 347Ч348 416 472
Krylov, subspaces 472 525 544ff
Lagrange multipliers 582
Lanczos methods for bidiagonalizing 495Ч496
Lanczos methods for least squares 496Ч498
Lanczos methods for singular values 495Ч496
Lanczos methods for symmetric indefinite problems 493Ч494
Lanczos methods for symmetric positive definite linear systems 490Ч493
Lanczos methods for unsymmetric eigenproblem 503Ч506
Lanczos tridiagonalization, block version 485Ч487 505
Lanczos tridiagonalization, complete reorthogonalization and 482
Lanczos tridiagonalization, conjugate gradients and 528
Lanczos tridiagonalization, interior eigenvalues and 478
Lanczos tridiagonalization, inverse eigenvalue problem and 623
Lanczos tridiagonalization, power method and 477
Lanczos tridiagonalization, practical 480
Lanczos tridiagonalization, Ritz pairs and 475
Lanczos tridiagonalization, roundoff and 481Ч482
Lanczos tridiagonalization, s-step 487
Lanczos tridiagonalization, selective orthogonalization and 483Ч484
Lanczos vectors 473
LAPACK xiii 2. 88 134Ч135 207Ч208 310 392Ч393 580
LDMT 135Ч138
Least squares problem, basic solution to 258Ч259
Least squares problem, equality constraints and 585Ч586
Least squares problem, full rank 236ff
Least squares problem, minimum norm solution to 256
Least squares problem, quadratic ineuqality constraint 580Ч582
Least squares problem, rank deficient 256ff
Least squares problem, residual of 237
Least squares problem, sensitivity of 242Ч244
Least squares problem, solution set of 256
Least squares problem, SVD and 257
Least squares solution via, fast Givens 241
Least squares solution via, Householder QR factorization 239
Least squares solution via, Lanczos 486
Least squares solution via, modified Gram Ч Schmidt 241
Least squares solution via, SVD 257
Length 210
Level of Operation 13
Level-3 fraction 92 146
Levinson algorithm 196
Linear equation sensitivity 80ff
Linear systems, banded systems 152ff
Linear systems, block tridiagonal systems 174Ч175 177Ч180
Linear systems, general systems 87ff
Linear systems, Hessenberg 154Ч155
Linear systems, Kronecker product 180Ч181
Linear systems, positive definite systems 142ff
Linear systems, symmetric indefinite systems 161ff
Linear systems, Toeplitz systems 193ff
Linear systems, triangular systems 88ff
Linear systems, tridiagonal 156Ч157
Linear systems, Vandermonde systems 183ff
LINPACK xiv
load balancing 280 282Ч283
Local program 285
Log of a matrix 566
Look-ahead 505
Loop reordering 9Ч13
Loss of orthogonality, Gram Ч Schmidt 232
Loss of orthogonality, Lanczos 481Ч482
LR iteration 335 361
LU factorization, band 152Ч153
LU factorization, block 101
LU factorization, determinant and 97Ч98
LU factorization, diagonal dominance and 119Ч120
LU factorization, differentiation of 103
| LU factorization, existence of 97Ч98
LU factorization, rectangular matrices and 102
M1NRES 494
Machine precision see УUnit roundoffФ
Mantissa 60
MATLAB xiv 88 134 207 309 392 556
Matrix functions 555ff
Matrix functions, integrating 569Ч570
Matrix functions, Jordan decomposition and 557Ч558
Matrix functions, polynomial evaluation 568Ч589
Matrix norms 54ff
Matrix norms, consistency 55
Matrix norms, Frobenius 55
Matrix norms, relations between 56
Matrix norms, subordinate 56
Matrix times matrix, block 25Ч27 29Ч30
Matrix times matrix, dot version 11
Matrix times matrix, outer product version 13
Matrix times matrix, parallel 292ff
Matrix times matrix, saxpy version 12
Matrix times matrix, shared memory 292Ч293
Matrix times matrix, torus 293Ч299
Matrix times vector 5Ч6
Matrix times vector, block version 28
Matrix, block 24ff
Matrix, differentation 51
Matrix, equations 13
Matrix, exponential 572ff
Matrix, functions 555ff
Matrix, inverse 50
Matrix, null space of 49
Matrix, operations with 3
Matrix, pencils 375
Matrix, powers 569
Matrix, range of 49
Matrix, rank of 49
Matrix, sign function 372
Matrix, transpose 3
Message-passing 276Ч277
Minimax theorem for singular values 449
Minimax theorem for symmetric eigenvalues 394
Mixed precision 127
Modified eigenproblems 621Ч623
Modified Gram Ч Schmidt 231Ч232 241
Modified LR algorithm 361
Moore Ч Penrose conditions 257Ч258
Multiple eigenvalues and Lanczos tridiagonalization 485
Multiple eigenvalues and matrix functions 560Ч561
Multiple right hand sides 91 121
Multiplicity of eigenvalues 316
Multipliers 96
Neighbor 276
NETLIB xiv
Network topology 276
Node program 285
Nonderogatory matrices 349
Nonsingular 50
Normal equations 237Ч239 545Ч547
Normal matrix 313Ч314
Normality and eigenvalue condition 323
Norms, matrix 54ff
Norms, vector 52ff
Notation, block, matrices 24Ч25
Notation, colon 7 19 27
Notation, matrix 3
Notation, submatrix 27
Notation, vector 4
Notation, x-o 16
NULL 49
Null space 49
Null space, intersection of 602Ч603
Numerical rank and SVD 260Ч262
OFF 426
Operation count see УWork or particular algorithmФ
Orthogonal basis 69
Orthogonal complement 69
Orthogonal iteration, Ritz acceleration and 422
Orthogonal iteration, symmetric 410Ч411
Orthogonal iteration, unsymmetric 332Ч334
Orthogonal matrix 208
Orthogonal matrix representations, factored form 212Ч213
Orthogonal matrix representations, Givens rotations 217Ч218
Orthogonal matrix representations, WY block form 213Ч215
Orthogonal projection 75
Orthogonal, Procrustes problem 601
Orthonormal basis computation 229Ч232
Orthonormality 69
Outer product 8
Overdetermined system 236
Overflow 61
Overwriting 23
p-norms 52
p-norms, minimization in 236
Pade approximation 572Ч574
Parallel computation, Cholesky, message passing ring 300
Parallel computation, divide and conquer 445Ч446
Parallel computation, gaxpy, message passing ring 279
Parallel computation, gaxpy, shared memory (dynamic) 289Ч290
Parallel computation, gaxpy, shared memory (static) 287
Parallel computation, Jacobi 431Ч434
Parallel computation, matrix multiplication, shared memory 292Ч293
Parallel computation, matrix multiplication, torus 293Ч299
Parlett Ч Reid method 162Ч163
Partitioned matrix 6
Pencils 375
Pencils, diagonalization of 461Ч462
Pencils, equivalence of 376
Pencils, symmetric-definite 461
Permutation matrices 109Ч110
Persymmetric matrix 193
Perturbation theory for eigenvalues 320Ч324
Perturbation theory for eigenvalues (symmetric case) 395Ч397
Perturbation theory for eigenvectors 326Ч327
Perturbation theory for eigenvectors (symmetric case) 399Ч400
Perturbation theory for generalized eigenvalue 377Ч378
Perturbation theory for invariant subspaces, symmetric case 397Ч399
Perturbation theory for invariant subspaces, unsymmetric case 324Ч325
Perturbation theory for least squares problem 242Ч244
Perturbation theory for linear equation problem 80ff
Perturbation theory for pseudo-inverse 258
Perturbation theory for singular subspace pair 450Ч451
Perturbation theory for singular values 449Ч450
Perturbation theory for underdetermined systems 272Ч273
Pipelining 35Ч36
Pivoting 109
Pivoting, Aasen 166
Pivoting, column 248Ч250
Pivoting, complete 117
Pivoting, partial 110
Pivoting, symmetric matrices and 148
Pivots 97
Pivots, condition and 107
Pivots, zero 103
Plane rotations see УGivens rotationsФ
Polar decomposition 149
Polynomial preconditioned 539Ч540
Positive definite systems 140Ч141
Positive definite systems, 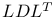 and 142 and 142
Positive definite systems, Gauss Ч Seidel and 512
Positive definite systems, properties of 141
Positive definite systems, unsymmetric 142
Power method 330Ч332
Power method, symmetric case 405Ч406
Power series of matrix 565
Powers of a matrix 569
Pre-conditioners, incomplete block 536Ч537
Pre-conditioners, incomplete Cholesky 535
Pre-conditioners, polynomial 539Ч540
Pre-conditioners, unsymmetric case 550
Preconditioned conjugate, gradient method 532ff
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 and
and