 131 302 333 335 343 425 131 302 333 335 343 425
 308 426 308 426
 421 421
 375 375
 372 ff. 432 372 ff. 432
 138 ff. 352 138 ff. 352
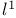 333 335 343 350 357 333 335 343 350 357
 283 404 424 283 404 424
 139 ff. 156 343 351 355 431 139 ff. 156 343 351 355 431
 , 0<p<1, 156 160 195 , 0<p<1, 156 160 195
 359 360 359 360
 137 359 431 137 359 431
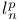 137 429 137 429
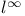 142 333 343 347 352 357 425 142 333 343 347 352 357 425
 283 363 424 283 363 424
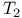 -space 3 -space 3
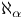 -compact 18 315 -compact 18 315
 -dual 405 -dual 405
 -dual 423 -dual 423
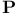 , , 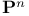 5 5
 8 8
 , ,  138 324 333 339 343 347 138 324 333 339 343 347
 8 8
 267 ff. 269 271 267 ff. 269 271
 267 ff. 269 271 267 ff. 269 271
 266 271 266 271
 380 380
 262 263 283 286 398 262 263 283 286 398
 256 257 263 277 285 286 300 370 385 400 436 256 257 263 277 285 286 300 370 385 400 436
 385 ff. 385 ff.
 263 264 273 278 385 389 263 264 273 278 385 389
 98 260 263 277 278 282 285 286 293 302 325 385 98 260 263 277 278 282 285 286 293 302 325 385
 115 115
 97 97
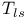 86 ff. 238 86 ff. 238
 300 300
 323 323
 234 238 248 276 277 285 286 354 234 238 248 276 277 285 286 354
 255 266 255 266
 , ,  56 70 75 119 122 151 155 243 248 268 287 391 406 431 432 56 70 75 119 122 151 155 243 248 268 287 391 406 431 432
 119 120 121 431 119 120 121 431
 304 370 304 370
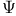 109 122 109 122
 -additive measure 426 -additive measure 426
 , ,  53 70 76 122 214 268 287 308 370 406 431 53 70 76 122 214 268 287 308 370 406 431
 119 120 431 119 120 431
 120 ff. 240 296 304 370 120 ff. 240 296 304 370
(B)-space 126 250 252 273 280 283 303 304 315 335 336 389 401 431
(DF)-space 396 ff. 401 434
(F)-norm 163 ff.
(F)-space 164 205 225 265 273 278 303 306 309 315 318 371 388 389 393 399 400 431
(FK)-space 424
(FM)-space 369 373 433
(LB)-space 223 ff. 434
(LF)-space 223 ff. 384
(M)-space 369 421 434
Absolute bipolar 246 249
Absolute polar 245
Absolutely convex 160 173 203
Absolutely convex about a point 175
Absolutely convex cover 173 ff. 240 325
Absolutely p-convex 160
Absolutely p-convex cover 160
Absorb 301
Absorbent 145
Accumulation point 4
Adherent point of a filter 12
Adherent point of a net 10
Adjoint mapping 73 197 237
Alaoglu — Bourbaki theorem 248 264
Alaoglu, L. 248
Alexandroff s theorem 21
Alexandroff, P. 21
Algebra 59
Algebraic basis 51 194
Algebraic boundary 177
Algebraic boundary point 177
Algebraic complement 51
Algebraic conjugate 69
Algebraic dimension 53 75
Algebraic dual 69 ff. 88 97 1O1 247
Algebraic hull 177
Algebraic interior point 177
Algebraic kernel 177
Algebraic point of smoothness 345
Algebraically closed 177 193 194
Algebraically closed convex  -body see “Convex -body see “Convex  -body” -body”
Algebraically closed half space 179 ff.
Algebraically isomorphic 53
Algebraically open 177
Algebraically open half space 179 ff.
Allen, H.S. 423
Almost constant sequence 89
Amemiya, I. 384 404 405 436
Anti-isomorphic 65
antisymmetric 9
Arens, R.F. 260 335
Associated bornological space 380
Asymptote 341
Automorphism 60
Baire, R. 27
Baire’s theorem 27
Ballier, F. 121
Banach algebra 130
Banach space 126
Banach — Dieudonne theorem 252 254 272
Banach — Mackey theorem 252 254
Banach — Schauder theorem 166
Banach — Steinhaus theorem 169
Banach — Stone Theorem 334
Banach, S. 165 168 170 189 259 272 350 431
Banach’s theorem 169
Barrel 257
Barrelled 257 261 297 305 306 367 369 371 372 380 434
Base of a uniform space 30
Base of neighborhoods 3
Basis of open sets 1
Bessaga, C. 166
Bidual 129 196 298 300 388
Bidual space see “Bidual”
Bilinear form 78
Bilinear functional 78
Bilinear mapping 78 171
Bipolar 246
Birkhoff, G. 11
Bohnenblust, H.F. 192
Boolean algebra 58
Bornological 379 ff. 387 388 399 400 403 419 434 436
Boundary 4
Boundary point 4
Bounded 24 152 248 254 403
Bounded above 9
Bounded below 9
Bounded closure 386 ff. 401
Boundedly closed 386 ff. 400
Bourbaki, N. 1 12 20 76 121 172 173 186 188 211 233 260 312 332 357 366 427 431 434
Bourbaki’s theorem 172
Bourgm, D.G. 159 162
Braconnier, J. 233
BV(I) 425
C 131
C(K), C(R) 138 250 323 334 335 343 350
Canonical mapping of E onto E/H 60
Canonical representation in the narrow sense 67
Canonical representation in the wide sense 67
Cantor, G. 25
Cartesian product 8
Cauchy filter 32 210
Cauchy net 32
Cauchy sequence 25
| CHARACTER 309
Characteristic function 41
Chillingworth, H.R. 423
Circled 146
Circled cover 146 174 241
Civin, P. 304
Clarkson, J.A. 353 357
Close of order N 29
Closed 321 322
Closed absolutely convex cover 175 (see also “Absolutely convex cover”)
Closed absolutely convex set see “Absolutely convex”
Closed ball of radius r 24
Closed convex cover 175 (see also “Convex cover”)
Closed convex set see “Convex”
Closed graph theorem 167
Closed linear subspace see “Linear subspace”
Closed mapping 6
Closed set 1
Closure 4
Closure point 4 312
Co-dimension 55
Co-echelon space 419 433
Co-echelon space, p-th order 420
Co-nullity 67
Coarser filter 12
Coarser topology 5
Coarser uniformity 30
Cofinal 10
Cofinal subnet 10
Collins, H.S. 269 271
column 63
Column-finite matrix 63
Compact 16 ff. 154 241 279 313 326 331 336 340 385 415
Compactum 26
Compatible 82 145
Compatible linear topology 236
Compatible locally convex topology 236 245 254 261
Complement of the image space 60
Complementary subspaces 51 95
Complemented lattice 58
complete 25 32 165 210 231 269 402 435 “Sequentially
Complete in itself 252
Complete lattice 57 85
Complete metric space 25 42
Complete metrizable vector space 166 ff. 172
Completely regular 45 47
Completion of a Hausdorff uniform space 33
Completion of a linearly topologized space 115 149
Completion of a locally convex space 208 248 261 269
Completion of a metric space 25
Completion of a topological vector space 148 158
Complex hyperplane 180
Complex linear functional 179
Complex locally convex space 273 ff.
Complex vector space 49
Cone 183 ff. 195 337
Cone generated by a set 184
Conjugate space 86 128
Connected 5 152
continuous 6
Continuous basis 101
Continuous bilinear mapping 171
Continuous dimension 101 102
Continuous linear functional 156 158
Continuous linear mapping 98 129 148 166 167 237 262 291 297 333 381
Continuous projection see “Projection”
Converge 10 12
Convergent sequence of matrices 107
Convex 160 173 186 194 244 273 322 336 337 343
Convex  -body 180—194 -body 180—194
Convex 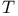 -body 180 182 187 188 193 342 -body 180 182 187 188 193 342
Convex algebraic body see “Convex  -body” -body”
Convex cover 173 ff. 240 245 321 322 325 331
Convex function 181
Convex-compact (weakly) 316
Cooke, R.G. 423
Cooper, J.L.B. 424
Coordinate space 405
Countability axioms 19 20
Countable at infinity 22
Countable degree 120 370
Countably compact 19 310 315
Cudia, D. 366
C[I] 138 197 260 430
Day, M. 157 317 318 360 361 363 366
Defect 55 67 103
Dense 4
Density zero 369
Diagonal 29
Diagonal transform 408
Diameter of a set 24
Diametrically opposite cone 183
Dieudonne, J. 48 85 113 121 272 274 311 318 354 369 370 371 372 384 387 404 419 421 424 432
DIMENSION see “Algebraic dimension” “Continuous
Direct product 76
Direct sum 54 57
Directed set 9
Discrete topology 4 82 83
Discrete uniformity 31
Distance between two points 23
Distance between two sets 24
Distinguished 306 ff. 399 400 435
Distributive lattice 58
Dixmier, J. 304 336 426
Donoghue, W.F. 392
Dual 86 128 275 298
Dual pair 85 234
Dual space see “Dual”
Dual system 70
Dually isomorphic lattices 57
E-bounded 251 254
Eberlein, W.F. 313
Eberlein’s theorem 313 317 326 366 415
Echelon space 419 433
Echelon space of p-th order 420
Eidelheit, M. 187
Embedding 60
Endomorphism 59
Equicontinuous 168 172 258 259
Equicontinuous bilinear mapping 171 ff.
Equivalent base of neighbourhoods 3
Equivalent defining system 216 227
Equivalent filter bases 12
Equivalent in the narrow sense 67
Equivalent in the wide sense 68
Equivalent linear mappings 67
Equivalent norms 125
Equivalent system of equations 105
Equivalent uniform spaces 30
Erdoes and Kaplansky’s theorem 75
Erdoes, P. 75
Essential supremum 142
Essentially bounded 142
Euclidean space 23
Everywhere dense 4
Exposed point 337
Exposed ray 341
Extension of a linear functional 70 86 188 233
Extension theorem see “Preceding entry”
Exterior point 4
Extreme point 330 337 338 340 346
Extreme ray 337
Fan, K. 366
Fantappie, L. 373
Fichtenholz, G. 425 427
Filter 11
Filter corresponding to a net 11
Filter-base 12
Finer filter 12
Finer topology 5
|
 |
|
О проекте
|
|
О проекте









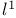




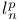
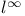

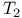 -space
-space 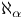 -compact
-compact  -dual
-dual  -dual
-dual 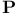 ,
, 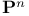

 ,
, 












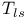




 ,
, 


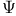
 -additive measure
-additive measure  ,
, 


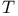 -body
-body