|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Köthe G. — Topological vector spaces I |
|
|
 |
| Предметный указатель |
Riesz — Fischer theorem 142
Riesz, F. 142 200 201
Riesz’s theorem 200
Right inverse 61 66
Right module 121
Right vector space 121
Ritzdorff, K. 122
Robertson, W. 157 211
Rolewicz, S. 161 162 166
Rotund 342
Row 63
Rudin, W. 353
Ruston, F. 336
Rutman, M.A. 336
Saturated 255
Saturated cover 256
Schatten, R. 336
Schauder, J. 166
Schwartz, L. 311 372
Sebastiao e Silva, J. 233 378
Second axiom of countability 20
Second category 28
Section 412
Sectional subspace 410
Semi-finite 109 112
Semi-norm 124 203
Semi-ordered 9
Semi-reflexive 298 304 305 306 307 315 319 320 322 355
Separable 26 126 128 259 260 271 273 280 283 362 370 371 398 400 401 403
Separated 3 187
Separately continuous 171 ff.
Separately equicontmuous 171 ff.
Separation theorem 187 ff. 243 322
Separation theorem for compact convex sets 243
Sequence spaces 405
Sequentially closed 273 313
Sequentially compact 19 310 313
Sequentially complete 89 210 295 296
Sequentially continuous 11 271 383
Set-theoretic product 8
Shirota, T. 380
Shortest distance 343 ff.
Shortness of a vector 106
Sierpinski, W. 165
Silva Dias, C.L. da 378
Similar automorphisms 121 ff.
Simply ordered 9
Small of order N 32
Smith, K.T. 392
Smooth 346 ff.
Smoothly normable 361 ff. 363
Smulian, V. 311 366
Smulian’s theorem 311
Sobczyk, A. 192 428 430
Solution of equations 103
Sphere 24
Square matrix 65
Steinhaus, H. 169
steps 419
Stone, M.H. 334
Straszewicz, S. 337
Strict (LB)-space 223
Strict (LF)-space 223 312 319
Strict closure point 296
Strict inductive limit 222 370
Strictly convex 342 346
Strictly normable 361 ff.
Strictly separated 187 243
Strong bidual 300
Strong derivative 364 ff.
Strong dual 115 257 306 388
Strong topology see “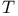 ” ”
Stronger topology 5
Strongly bounded 251 252 254
Strongly differentiable 364
Strongly inaccessible 392
Strongly reflexive 115 118
Strongly semi-reflexive 115
Sub-additive 180 188
Sub-base 12
Sub-basis 1
subspace see “Linear subspace”
Subspace of an involution 428
Sum of mappings 59
Sum of matrices 64
Sum of subspaces 54 152 154 322
Summable 139
Support manifold 330
Supporting facet 336
Supporting hyperplane 193 ff. 244 245 320 349
Symmetric mapping 122
Symmetric sequence space 409
Symmetric vicinity 30
Sz.-Nagy, B. 201
Takenouchi, O. 233
Tangent hyperplane 346
Tensor product 76
Theorem of Alaoglu — Bourbaki 248 264
Theorem of Alexandroff 21
Theorem of Baire 27
Theorem of Banach — Dieudonne 252 254 272
Theorem of Banach — Mackey 252 254
Theorem of Banach — Schauder 166
Theorem of Banach — Steinhaus 169
Theorem of Banach — Stone 334
Theorem of bipolars 246
| Theorem of Bourbaki 172
Theorem of Eberlein 313 317 326 366 415
Theorem of Erdoes and Kaplansky 75
Theorem of Grothendieck 269
Theorem of Hahn — Banach 188 ff. 196
Theorem of Kaplansky 312
Theorem of Klee 319 ff.
Theorem of Krein 325 326 336
Theorem of Krein — Milman 331 336 339
Theorem of Lebesgue 324
Theorem of Lefschetz 109 115
Theorem of Mackey 254
Theorem of Mackey — Arens 98 260
Theorem of Mackey — Ulam 392
Theorem of Milman 332 341
Theorem of Milman — Rutman 336 337
Theorem of Montel 373
Theorem of Pontryagin 310
Theorem of Ptak 326
Theorem of Riesz 200
Theorem of Riesz — Fischer 142
Theorem of Smulian 311
Theorem of Tychonoff 18 96
Theorem of Urysohn 44 45
Tillmann, H.G. 378
Toeplitz, O. 48 113 252 378 421 423 432
Topological complement 92 95 99 109 121 156 158 168 238 239 240 424 426
Topological direct sum 84 117 214 288 308
Topological group (abelian) 309
Topological homomorphism 91 150 166
Topological inductive limit 220 224 289 290 403
Topological isomorphism 84 91 125 150
Topological linear space 145
Topological monomorphism 91 150
Topological product 7 8 117 127 149 207 283 296 299 303 368 370 384 389
Topological projective limit 230 ff. 290 294 300
Topological space 1
Topological sum 100
Topological vector space 83 145
Topologically isomorphic 84 125
topology 1
Topology of a uniform space 30
Topology of pointwise convergence see “ ” ”
Topology of precompact convergence see “ ” ”
Topology of uniform convergence on 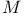 255 255
total 132 237 255
Totally bounded 26 36
Totally disconnected 6 83
Totally ordered 9
Transitive 9 227
Translation-invariant 124 147 164
Transposed equation 103
Transposed matrix 74
Triangular matrix 106
Trivial topology 5
Truncated cone 183
Tychonoff space 45
Tychonoff, A. 45 151
Tychonoff’s theorem 18 96
Ulam, S. 392
Ulm, H. 122
Ultrafilter 14
Uniform norm topology 130
Uniform space 29 47
Uniformity 29 386
Uniformizable 43 147
Uniformly continuous 24 32 265
Uniformly convex 353 360 365 366
Uniformly equicontinuous 168
Uniformly normable 361 ff.
Uniformly smooth 363 ff.
Uniformly strongly differentiable 364
Union,  57 57
Unionof topologies 5
Upper bound 9
Upper limit 39
Upper semi-continuous 40
Urysohn, P. 42
Urysohn’s embedding theorem 45
Urysohn’s extension theorem 44
Urysohn’s lemma 42
Variation 425
Vector 48
Vector space 48
Vertex 183
Vicinities 29
Vilenkin, N.Y. 121
Weak derivative 349 ff.
Weak dual 235
Weak neighbourhood 85
Weak topology see “ ” ”
Weaker topology 5
Weakly complete 89 248
Weakly continuous 237
Weakly convex-compact 316
Weakly differentiable 349
Weakly partially compact 317
Weakly precompact 248
Weil, A. 29 233
Well-ordered 9
Yood, B. 304
Yosida, K. 425
Zelinsky, D. 121
Zeller, K. 424
Zorn, M. 9
Zorn’s Lemma 9 10
“sliding hump” 252 281
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



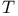 ”
” ”
” ”
”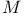

 ”
”