Авторизация
Поиск по указателям
Kaye R. — Models of Peano Arithmetic
Обсудите книгу на научном форуме Нашли опечатку?
Название: Models of Peano ArithmeticАвтор: Kaye R. Аннотация: Non-standard models of arithmetic are of interest to mathematicians through the presence of infinite integers and the various properties they inherit from the finite integers. Since their introduction in the 1930s, they have come to play an important role in model theory, and in combinatorics through independence results such as the Paris-Harrington theorem. This book is an introduction to these developments, and stresses the interplay between the first-order theory, recursion-theoretic aspects, and the structural properties of these models. Prerequisites for an understanding of the text have been kept to a minimum, these being a basic grounding in elementary model theory and a familiarity with the notions of recursive, primitive recursive, and r.e. sets. Consequently, the book is suitable for postgraduate students coming to the subject for the first time, and a number of exercises of varying degrees of difficulty will help to further the reader's understanding.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1991Количество страниц: 292Добавлена в каталог: 02.07.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
54 6 30 7 30 24 12 72 69 13 44 47 16 10 3 73 45 5 54 1 64 273 1 7 29 70 73 83 269 271 273 23 78-9 20 31 5 101 (see also 10 10 6 181—5 263 268 39 259 90 101 165 247 251 1 23 78—9 218 275 7 166 185 79 116 126 7 128—9 167 (see also Satisfaction short Type) 2 25 12 21 23 78—9 274 248 274 25 27 36 40 (see Satisfaction Satisfaction Type) 79 116 126 2 146—52 223 269 2 152 2 96 130—4 2 128—9 2 166 269 2 79 43 10 17 2 * (against exercise numbers) 1 1-consistency (of PA, 218 <,...,> 31 <,> (pairing function) 30 Absoluteness 24 Ackermann function 68 Adamowicz, Z. 269 Admissible set 272 Ajtai, M. 274 Algebraic fragments of arithmetic 267 Arithmetic completeness theorem 186 190—2 223 225 Arithmetic hierarchy 78—81 127 Arithmetic models 186 Arithmetic structures 186 Atomic sentence 236 Automorphism 93 259—61 272-3 Axiom 3 Axiom of collection 33 81 Axiom of definition 47 Axiom of induction 43 Axiom of second-order collection 102 Axiom of second-order induction 42 46 Axiom of total induction 45 (see also Least-number principle) Axiomatizability, 134 Axiomatizability, finite, of 134 Axiomatizability, non-finite, of PA 132 Axiomatizability, recursive 39 43 Barwise, J. 184 248 272 273 Bennett, R. 271 Bennett’s 271 273—4 Bezout’s Theorem 55 Binary tree (see Tree) Block of quantifiers 79 81 Boolean operations 2 Bounded minimalization 7 30 Bounded quantifier 23 78 81 Bounded quantifier, closure under 82 Buss, S. 274 Canonical term 128 233 274 Cantor 75 Cantor Normal Form 221 Card(W) 2 Cardinal 1 Cardinality of a Model 2 Cases, definition bv 7 Cegieiski, P. 267—8 Chain of Models 5 Characteristic function 7 29 Chinese remainder theorem 58 65 Chronic resplendency 252 273 Church — Turing thesis 8 Code of 0s and 1s 172—3 Code of a function 143—5 Code of a sequence 31 58 60 64 Code of a set 13—14 141 172 261 Code of a tuple 30—1 (see also Dyadic coding Goedel-numbering type coded) Cofinal extensions 86—90 Cofinal subset 86 Collection axioms 33 81—6 Collection axioms, in set theory 78 Collection axioms, parameter-free 134 Collection axioms, second-order 102 Compactness Theorem 3 Complete diagram 4 Complete theory 39 Complete type 94 147 Completeness theorem 3 (see also Arithmetized completeness theorem) Composition (of functions) 6 Computable set 5 Congruence 54 Conservation results 271—2 Conservative extension of a model 100—1 Conservative extension of a theory 51 Conservative extension, 137 272 Consistency 4 41 Consistency of 138 140 218 Consistency of PA 41 218 223 233 246 Consistency, 1-consistency 236 Consistency, FA -consistency 236 Consistency, simple consistency 38 Constant 2 Cook, S. 274 Coprimality 55 Craigs trick 155 Cut 22—3 70 76 194 269—70 Cut Elimination Theorem 140 Cut rule 118 140 238 Davis, M. 88 Dedekind, R. 42 Deduction Theorem 237 Definable elements 91—6 (see also Definable type 102 Defining axiom 47 Definition by cases 7 Definition of truth 3 104 223 225—6 Degree of a model 268 Dense linear order 75 265 Diagonalization 37 Diagram 4 Dimitracopoulos, C. 269 271 274 Discrete linear order 18 73 157 265 Divisability 54 Division 53—4 DLO (dense linear order) 75 Domain (of a model) 2 Downward Loewenheim — Skolem theorem 4 223 Dyadic coding 173—4 Ehrenfeucht, A. 261 267 268 Elementary chain (of models) 5 Elementary end-extension 90 96—103 152 165 247 Embedding 159 389 Empty sequence 172 End-extension 12 21 90 192 205 268—9 Initial Engeler, E. 273 Eq(x, y) (equality function) 7 Equality Axioms 117 Euclidean division 53 Evaluation of terms 119 Existential ( 3 Expansion (of a model) 3 248 252 exponentiation 67 73 274 Exponentiation, Bennett’s 271 273—4 Extended Grzegorczyk hierarchy 220—1 271 Extension (of a model) 4 Extension (of a model), cofinal 86 Extension (of a model), conservative 100—1 Extension (of a model), elementary for formulas in 24 (see also Elementary end-extension End-extension) FA-consistent 236 Factorial 66 Finite approximation 234—5 Finite sequences 31 Finite sequences of 0s and 1s 168 172 Code First-order language (see Language) Formula 88 Formula, 23 78—9 Formula, 79 116 Formula, finitely satisfied set of 146 Formula, NP 274 Formula, strict 82 85 116 Formula, unique readability of 115 Fragments of PA 43 81—6 130—140 271-2 Open Fraisse, R. 273 Free-variable 3 116—17 Friedman, H. (v) 137 159 184 268 270 Friedman’s theorem 160 164—5 197 247 269 Function 2 Fundamental sequence (of an ordinal) 221 Gaifman, H. (v) 87 89 96 101 268—9 271 Gaifman’s splitting theorm 89 90 Goedel — Rosser incompleteness theorem 38—9 153 154—5 157 178 189-90 Goedel's 64 273 Goedel's completeness theorem 3 Goedel, K. (v) 3 31 35 39 218 Goedel-numbering 37 108—10 148 153 224—5 Goedel’s compactness theroem 3 Goedel’s first incompleteness theorem 39 218 Goedel’s lemma 31 35 58—64 Goedel’s second incompleteness theorem 41 218 Goodstein sequences 220 Goodstein, R.L. 220 Graph of a function 31 Grzegorczyk hierarchy 220—1 271 Hajek, P. 271 Hardy, G.H. 53 Harrington, L. (v) 193 270 Paris-Harrington Henkin-style proof 178 Hercules and the hydra 218—19 Hierarchy of 79—80 104-5 127—8 Hilbert’s irreducibility theorem 267 Hilbert’s Tenth Problem 88 267 Hodges, W. 103 266 Homogeneous model 259 265 Homogeneous set 208 Incompleteness theorem 35—41 132 218 incompleteness Goedel's Goedel’s Indicator 193 270 Indicator for 197 204 205 Indicator for initial segments isomorphic to the model 197 Indicator for initial segments satisfying coded theories 203 Indicator for intitial segments having certain expansions 264—5 Indicator for recursively saturated initial segments 204—5 265 Indicator, well-behaved 194 197 270 Indiscernible sequence 207 273 Induction axiom, first-order 43 Induction axiom, open 267 Induction axiom, second-order 42 46 Induction axiom, total induction 45 Inference (in a proof) 118 Infinitude of primes 65—7 70 Initial segment 12 21 69 159 264—5 Initial segment, coded 206 Initial segment, elementary 134—40 164 197 204 205 End-extension Indicator) Initial segment, isomorphic to the model (see Friedman’s theorem) Initial segment, recursively saturated 204—5 265 Integer part (after division) 54 Integral domain 21 Interesting number 95 Interpretation 3 Interpretation, strong 190—2 225 Inverse modulo x 56 Irreducible 2 55—8 Jensen, D. 261 267 268 Joint consistency test 253 Kanamori - McAloon principle 208—18 247 Kanamori, A. 208 218 270 Kaufmann, M. 269 Kaye, R. 267 272 273 Ketonen, J. 221 270 Kirby, L. (v) 133 138 193 220 269 270 Kleene's theorem 254 Kleene, S.C. 127 254 Knight, J.F. 268 269 Koenig’s lemma 173 Kossak, R. 272 273 Kotiarski, H. (v) 233 272 273 Krajewski, S. (v) 233 272 Krajfdek, J. 274 275 Lachlan, A. (v) 228 233 272 Lachlan’s theorem 228—33 Language 2 Language of arithmetic 10 16 Language, Godel-numbering of (see Goedel-numbering) Language, recursive 147 152—3 Language, recursive extensions of 179 185 Language, satisfaction class for 224 246 252 Language, symbols of 2 Largeness properties 221—2 Larski s theorem on the undelinabilitv of truth 28 40 223 Least-number principle 44 95—6 Length (of a sequence) 105 172 Lesan 11 (see Lessan H.) Lessan. H. 138 267 Linear order, dense 75 265 Linear order, discrete 18 73 157 265 Lipshitz, L. 267 Loeb. M.H. 220 Loewenheim — Skolem theorems 4 223 Logical symbol 2 Lt(x, y) (less-than function) 7 M-consistent 236 M-finite 64 65 M-rule 247
Реклама
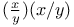
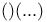(mimmalization) 
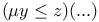(bounded minimalization)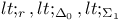 
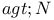(a is nonstandaid) 
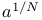(initial segment) 
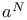(initial segment) 
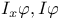(induction axiom) 
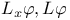(least-number principle) 
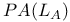(extension of PA)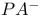 
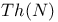(true arithmetic) 
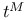(value of a closed term) 
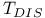(discrete linear order) 
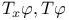(axiom of total induction) 
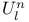(projection function) ![$[\frac{x}{y}][x/y]$](/math_tex/8397ac2af6a75122cbcd1d2765b3b51b82.gif)
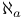(cardinal) 
-function 
(end of proof)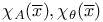 
(characteristic function) 
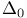induction 
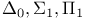(formula classes)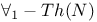 
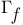(graph of 
) 
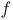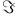(paitial recursive functions) 
-like model 
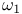-like model)
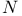(standard model) 
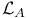(language of arithmetic) 
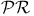(primitive recursive (unctions) 
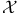-saturated 
-consistent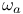 
(initial ordinal) 
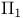formula 
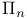Formula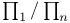 
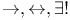
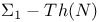
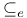(end-extension/mitial segment) 
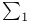formula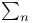 
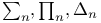(formula classes) 
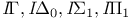(theories)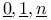 
) 
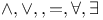
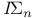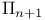of 
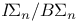
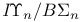
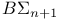over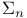 
-definable elements)
, 
, 
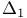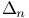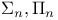
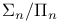formulas 
|
|
О проекте