Авторизация
Поиск по указателям
Kaye R. — Models of Peano Arithmetic
Обсудите книгу на научном форуме Нашли опечатку?
Название: Models of Peano ArithmeticАвтор: Kaye R. Аннотация: Non-standard models of arithmetic are of interest to mathematicians through the presence of infinite integers and the various properties they inherit from the finite integers. Since their introduction in the 1930s, they have come to play an important role in model theory, and in combinatorics through independence results such as the Paris-Harrington theorem. This book is an introduction to these developments, and stresses the interplay between the first-order theory, recursion-theoretic aspects, and the structural properties of these models. Prerequisites for an understanding of the text have been kept to a minimum, these being a basic grounding in elementary model theory and a familiarity with the notions of recursive, primitive recursive, and r.e. sets. Consequently, the book is suitable for postgraduate students coming to the subject for the first time, and a number of exercises of varying degrees of difficulty will help to further the reader's understanding.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1991Количество страниц: 292Добавлена в каталог: 02.07.2010Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
MacDowell (v) 96 MacDowell — Specker theorem 96 Macintyre, A. 267 268 270 274 Macpherson, H.D. 272—3 Mal’cev, A.I. 267 Marker, D. 267 268 Matijasevic, Yu. V. 88 Max(...) (maximum) 6 17 Maximum 6 17 McAloon, K. 156 208 218 267 270 274 Mills. G. 270 Min(...) (minimum) 7 17 Min-homogeneous set 208 Minimal extension 268—9 Minimal model 93 Minimali/ation 6 30 Minimum 7 17 Model 2 Model, 101 Model, 181—5 263 268 Model, 259 Model, 90 101 165 247 251 Model, 147 150—3 269 Model, 152 Model, arithmetic 186 188 Model, cardinal of 2 Model, chronically resplendent 252 Model, degree of 268 Model, homogeneous 259 265 Model, minimal y 3 Model, prime 92 Model, recursive 153 265 267 Model, recursively saturated 147 148—50 181 184 223—65 272-3 Model, resplendent 245 248 247—65 Model, rigid 93 Model, short 152 Model, short 166 269 Model, short-recursively saturated 152 2 Model, tail 152 Modified subtraction 6 19 Modulus 54 Morgenstern, C. 270 MRDP theorem 88 157 274 Multiplicative inverse 56 Murawski, R. 272 Nadel, M. 267 268 Natural deduction 117—19 140 Nelson, E. 271 274 Nonlogical symbol 2 Nonstandard element 11 Nonstandard methods 13 266—7 Nonstandard model 10 Nonstandard model of set theory 223 226 247 265 Nonstandard number 11 Nonstandard structure 10 NP formula, predicate 274 Omitting types theorem 93—5 Open induction 267 Oracle 9 34—5 174-5 Order, dense linear 75 Order, discrete linear 18 73 157 Order-type of a model of arithmetic 75 Ordered ring 20 Overspill 70 71 72 223 Overspill for the standard cut 72 77 155 P = NP problem 274 PA(S) 246—7 Pairing function 62—3 80 Parameter-free collection 134 Parameter-free induction 95—6 Parameter-free PA 95—6 Parameter-free teast-number principle 95—6 Parikh, K 73 273 Parikh’s theorem 70 73 273 Paris — Harrington principle 208 223 247 270 Paris — Harrington Theorem 206 270 Paris, J. (v) (vi) 133 137 138 193 208 218 267 269 270 271 274 Parsons, C. 133 Partial recursive function 5 Path 173 Peano, G 42 Peano-tike theorv 96 Phillips, R.G. 269 Pigeonhole Principle 68 274 Presburger, M. 267 Prime model 92 Prime numbers 21 55—8 Prime numbers, infinitude of 65—7 70 Primitive recursion 6 67 Primitive recursion in an oracle 9 Primitive recursive function 6 67 271 Primitive recursive set 7 67 proof 3 117—19 177—8 251 Provability predicate 41 119 Provably recursive function 51—2 67 194—6 Provably recursive relation 51—2 67 271 Pudlak, P. 274 275 Putnam, H. 88 q 26 46 Q (theory) 26 Quantifier 2 Quantifier for ‘unboundedly many‘ 96—7 Quantifier, block of 79 81 Quantifier, bounded 23 Quantifier, Ramsey 270 Quantifier, ‘part-of‘ 35 107 Quine, W. v.O. 35 Quinsey, J. 218 R 40 R (theory) 30 R, 1 (Godel-numbering) 37 108-10 R.e. set 8 Rabin, M. 269 Rabin’s theorem 269 Ramsey quantifier 270 Ramsey, F. 207 Ramsey’s theorem 207—8 213 Ratajczyk. Z. 272 Readability of formulas 115 237 Readability of terms 111 237 Recursive extension of a language 179 185 Recursive function 7 Recursive language 147 152—3 Recursive model 153 265 267 Recursive saturation 147 148—50 181 184 223—65 272-3 Recursive saturation, 265 Recursive set 5 7 Recursively enumerable set 8 Recursively inseparable sets 154 Reduct (of a model) 3 246 267 Refinement (of a finite approximation) 235—6 Relation 2 Relative recursion 9 34—5 174-5 Remainder after division 54 Representation (in a theory) of a function or set 35—6 41 Resplendency 245 248 Ressayre, J. P. 184 248 Restriction (of a sequence) 106 172 Rich theory 261 264 268 Ring, discretely ordered 18—19 Ring, ordered 20 (see also Integral domain) Robinson, A. (v) 70 266—7 272 Robinson, J. 88 Roquette, P. 267 Rosser, J.B. 28 39 Ryll — Nardzewski, C. 132 273 S (successor function) 5 15 47 5 S (theory) 27 S(x) (successor of A) 5 S.t., iff 1 Satisfaction class 224—5 252 255-6 Satisfaction class for languages extending 246 252 Satisfaction class, 245 Satisfaction class, full 224 233 Satisfaction class, full inductive 223 233 272 Satisfaction class, inductive 225 245 Satisfaction class, partial 225 228 Satisfaction class, partial inductive 225 226—8 257 Satisfaction class, standard 224 225 Satisfaction for 122—6 246 Satisfaction for 104 126—7 223 224 228 Saturation 269 (see also Recursive saturation Schmerl, J. H. 269 270 272 273 Scott set 174 178 184 186 262—5 268 Scott, D. (v) 174 184 Second-Order Arithmetic 42 27 Second-order collection axiom 102 Second-order induction axiom 42 46 Sequence of 0s and 1s 168 172 Sequence, codes for 31 58 60 64 Sequence, empty 172 Sequence, indiscernible 207 273 Sequence, restrictions of 106 172 Sequence, sequent 117 Set theory, models of negation of axiom of infinity 146 Set theory, models of nonstandard 223 226 247 265 Set, code for 13—14 141—8 172 Shelah, S. 275 Shepherdson, J. 267 Short 166 269 Short recursive saturation 152 2 Shortness 152 Simmons, H. 193 Simple consistency 38 Simpson, S.G. 270 Skolem, T. (v) 4 10 267 Smith. S.T. 247 272 Smorynski — Stavi theorem 205 Smoryriski, C. 205 265 Smullyan, R. 35 Solovay, R. M 221 270 Specker, E. (v) 96 Stability theory 269 Standard model 10 Standard satisfaction class 224 225 Standard system 141 151—2 159 61-4 268 Stavi, J. 205 Strong interpretation 190—2 225 Structure 2 (see also Model) Submodel (see Substructure) Substitution for a variable 116—17 Substring 35 107 Substructure, elementary 4 Substructure, isomorphic 264 (see also Initial segment Friedman’s Subtraction 6 19 Svenonius, L. 273 Symbiosis 2 Takeuti, G. 275 Tallness 152 (see also Tarski 40 178 316—7 Tarski — Vaught test 4 Tarski — Vaught test for 26 Tarski — Vaught test for 86 Tarski — Vaught test for template (for an 240 Tarski’s definition of truth 3 104 23 225—6 Tennenbaum, S. 153 Tennenbaum’s theorem 153—4 157 178 189—90 267 268 Term 110 148 Term, canonical 128 Term, evaluation of 119—21 Term, unique readability of 111 Theory 3 Total induction 45 TREE 173—4 True arithmetic 10 Truth 10 (see also Tarski) Tuple 12 (see also Code of a tuple) Turing 8 Turing degrees of a model 268 TYPE 94 146 Type of a tuple 182 258 Type, 146 160 Type, coded 160 263 Type, complete 94 147 Type, definable 102 Type, omitted 94 Type, over a theory 93—4 Type, over model 146 Type, primitive recursive 149—50 Type, principal 94 Type, r.e 149—50 Type, realized 94 Type, recursive 141 146 146 160 Underspill 70 Unique readability of formulas 115 237 Unique readability of terms 111 237 Universal 20 90 Upward Loewenheim — Skolem theorem 4 V, (the 2 Value of a term 119 Van den Dries. L. 267 Variable 2 148 Variable, substitution of 116—7 Vaught, R L. (see Tarski-Vaught test) Wainer, S. 220 Wiikie. A. 70 267 269 271 274 Wilmers. (i 181 182 184 267—8 272 Woods. A. 274 X - y (modified subtraction) 6 ‘part-of‘ quantitication 107 ‘part-of‘ relation 35 107
Реклама
-like 
-saturated 
-homogeneous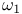 
-like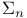 
-recursively saturated 
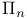-recursively saturated 
sentence for 
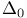formulas 
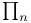-recursive saturation 
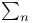-tallness)
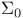formulas 
proof) 
formula 
variable) 
|
|
О проекте