Авторизация
Поиск по указателям
Ames W.F. — Numerical methods for Partial Differential Equations
Обсудите книгу на научном форуме Нашли опечатку?
Название: Numerical methods for Partial Differential EquationsАвтор: Ames W.F. Аннотация: This volume is designed as an introduction to the concepts of modern numerical analysis as they apply to partial differential equations. The book contains many practical problems and their solutions, but at the same time, strives to expose the pitfalls — such as overstability, consistency requirements, and the danger of extrapolation to nonlinear problems methods used on linear problems. Numerical Methods for Partial Differential Equations, Third Edition reflects the great accomplishments that have taken place in scientific computation in the fifteen years since the Second Edition was published. This new edition is a drastic revision of the previous one, with new material on boundary elements, spectral methods, the methods of lines, and invariant methods. At the same time, the new edition retains the self-contained nature of the older version, and shares the clarity of its exposition and the integrity of its presentation.
Язык: Рубрика: Математика /Численные методы /Численный анализ /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Second EditionГод издания: 1977Количество страниц: 367Добавлена в каталог: 18.02.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Explicit-implicit methods for two space variables 227 Explicit-implicit methods, advantages of 225 Extrapolation technique, 247 Fairweather, G. 156 157 163 164 255 313 Fast Fourier Transform 304—307 Fast method, for Fourier series 305—307 Feller, W. 25 40 Ferguson, N. B. 337 350 Finite difference approximations, on nonuniform grid 275-278 Finite difference operators, averaging 20 Finite difference operators, backward 19 Finite difference operators, central difference 20 Finite difference operators, forward 19 Finite difference operators, shift 20 Finite elements 342—348 Finite elements by Bubnov — Galerkin method 344—348 Finite elements, final equations 347 Finite elements, geometry 343 Finite elements, node 344 Finite elements, triangular 344 Finite elements, weak solutions 345 Finlayson, B. A. 320 321 324 328 333 348 349 First-order method for conservation laws 222 First-order method, Lax 222 First-order method, stability limit 222 Fischer, J. 159 164 Fisher, G. D. 259 314 Fix, G. 343 350 Forsythe, G. E. 15 29 33 39 40 56 65 76 91 104 107 108 135 146 162 163 249 260(79) 276 313 Forward and backward space differences, method 211 Forward difference 22 Fourier analysis cyclic reduction for Poisson equation 306 307 Fourier series, discrete 304 Fourier stability analysis 195 Fourier stability analysis for hopscotch methods 222 223 Fourier stability analysis for vorticity equation 287 Fourier transform, fast 304—307 Fox, L. 2 33 39 40 42 85 90 241 242 252 260 300 312 Fractional steps method 307—311 Fractional steps method, approximate factorization 309 310 Fractional steps method, not approximation to solution 308 Fractional steps method, splitting method a la Yanenko 307—310 Fractional steps method, stabilizing corrections 307 (see also “Alternating direction implicit methods”) Frank, R. M. 263 315 Frank, T. G. 101 130 139 144 161 Frankel, S. P. 2 39 61 106 150 162 163 Frazer, R. A. 322 349 Friberg, J. 200 228 Friedman, A. 42 74 90 Friedman, B. 106 145 162 Friedrichs, K. O. 1 39 167 179 194 205(14) 212 227 228 238 240 265 312 315 Fromm, J. E. 283 289 290 294(186) 316 318 Galerkin method see “Bubnov — Galerkin method” Galerkin, B. G. 323 349 Garabedian, P. R. 93 125 162 167 227 Garabedian, successive over-relaxation method 125 Garder, A. O. 156(71) 163 255(56) 313 Gary, J. 219 221 229 Gas combustion in rocket 76 Gas dynamics, Eulerian form 212 213 216 Gas dynamics, implicit method for 272 Gas dynamics, Lagrangian form 213 220 272 Gas dynamics, one space variable 212—221 Gas dynamics, typical boundary conditions 220 Gas flow, characteristics solution 186—191 Gas flow, closed type 267 Gas flow, subsonic 9 Gas flow, supersonic 9 Gas flow, transonic 9 Gas flow, two dimensions 8 Gates, L. D. 106 145 162 Gaunt, J. A. 247 313 Gauss — Seidel iteration, column iteration 148 Gauss — Seidel iteration, convergence of 110—113 Gauss — Seidel iteration, lines 148 Gauss — Seidel iteration, rate of convergence 117 Gauss — Seidel iteration, row iteration 145 Gauss — Seidel iteration, spectral radius 114 118 Gauss — Seidel iteration, symmetric positive-definite systems 113 Gaussian (normal) distribution, probability density function 25 Gear, C. W. 302 319 Geiringer, H. 101 103 161 General solution 92 Gentry, R. A. 302 318 Gere, J. M 245 312 Gerling, C. L. 104 161 Gerschgorin, S. 31 Giaquinta, A. R. 283 285 317 Giese, J. H. 33 40 282 317 Ginsburg, T. 275(130) 316 Givens, W. 248 313 Godunov, S. K. 241 243 312 Golub, G. H. 141 143 163 Goodier, J. K 97 161 324 349 Gourlay, A. R. 219 221 222 223 229 265 315 Gradient 41 Greenberger, M 301(202) 318 Greenspan, D. 236 258 259 283 311 313 314 316 Green’s function, discrete analogue 302 Green’s Theorem 276 Griffin, D. S. 275 278 316 Guillemin, E. A. 114 Gunn, J. E. 259 314 Gustavson, F. 98 Gustin, W. 260(76) 314 Haack, W. 262 314 Habetler, G. J. 153 Hadamard, J. 41 90 94(2) 161 Hageman, L. A. 125 Hall, T. 322 349 Hamielec, A. R. 290 318 Hamming, R. W. 85 91 Harlow, F. H. 283 289 291 291(182) 294 302(201a) 316 318 Harrington, R. F. 331 349 Hartnett, J. P. 74 77 79 91 Hartree method, first-order equations 209 210 Hartree, D. R. 209 228 Haviland, J. K. 301 302 318 Hayashi, S. 149 156(63) 163 Head of rarefaction wave 238 Heliums, J. D. 283 289 291 294 295 298 317 Heller, J. 274 315 Higgins, T. J. 2 39 Hilbert, D. 41 90 167 173 227 245 246 262 312 314 Hildebrand, F. B. 20 24 32 40 44 90 326 349 Hill, R. 10 Hindmarsh, A. C 302 319 Hirasaki, G. J. 295 318 Hirt, C. W. 291 Hockney, R. W. 306 307 319 Hoffman, T. W. 290(179) 318 Holmboe, J. 260 314 Holt, M. 290 318 Hopscotch method for conservation laws 221—224 Hopscotch method for conservation laws, explicit Lax 222 Hopscotch method for conservation laws, fast version 223 Hopscotch method for conservation laws, Lax — Wendroff 223 224 Houghton, D. D. 304 319 Householder, A. S. 98 109 161 162 Howarth, L. 77 91 Hrenikoff, A. 320 348 Hubbard, B. E. 156 163 238(13) 312 Hugoniot conditions for shocks 240 Hung, T. K. 289 317 Hyman, M. A. 2 39 50 51 91 200(19) 228 Hyperbolic equations 4 Hyperbolic equations, error analyses 194 196 Hyperbolic equations, higher dimensions 262—270 Hyperbolic equations, higher dimensions, characteristics 262 Hyperbolic equations, higher dimensions, finite difference methods 263—265 Hyperbolic equations, higher dimensions, Lax — Wendroff method 264 265 Hyperbolic equations, implicit methods 199—201 Hyperbolic equations, nonlinear 201 203 Hyperbolic equations, overstability 197—199 Hyperbolic equations, singularities 265—270 Hyperbolic equations, stability 200 Hyperbolic equations, three levels 200 Hyperbolic equations, time quasilinear 202 203 Hyperbolic equations, von Neumann form 200 Implicit method, conservation laws 225 Implicit method, diffusion equation 49—51 Implicit method, matrix stability analysis 60 61 Implicit method, nonlinear parabolic equations 82 Implicit method, three level 60 Improperly posed problems, Laplace equations 94 Initial boundary value problems 4 Initial data, relation to characteristics 169 Initial value problem, pure parabolic 62 Initial value problem, transformation 62 Instability, control by artificial viscosity 87 Instability, numerical 28 Instability, physical 28 Integral method 323 Integration domain 36 37 Integration technique, irregularly shaped regions using nonuniform mesh 276—278 Interfaces 238 Interfaces, numerical calculation 239 Interpolation polynomial, Lagrange 243 Interpolation, linear 81 Interpolation, quadratic 81 Interval of dependence 195 Inverse iteration, convergence 249 Inverse iteration, properties 249 Inverse iteration, relation to power method 251 Irregular mesh point 79 Isaacson, E. 209(28) 211(28) 214(28) 219(28) 228 Israeli, M. 299 318 Iteration parameters, alternating direction 149 Iteration, block 100 Iteration, consistency condition 99 Iteration, convergence 109 110 Iteration, degree 99 Iteration, inner 82 133 158 250 Iteration, inner-outer 278 Iteration, linear 99 139 Iteration, outer 133 250 260 261 Iteration, Picard outer 158 Iteration, point 99 Iteration, stationary 99 139 Jackson, D. 326 349 Jackson, R. F. 159(90) 164 234(4) 311 Jacobi line iteration 145 148 Jacobi point iteration, convergence 110—112 Jacobi point iteration, rate of convergence 117 Jacobi, C. G. 103 Jaeger, J. C. 35 40 42 90 Jain, P. C. 283(151) 316 Jarvis, P. H. 275(133) 316 Jeffrey, A. 6 39 179 186 227 265 266 270 315 Jeffreys, H. 10 40 John, F. 29 40 65 91 Johnson, N. L. 27 40 Jones, B. F. 85 86 91 Jones, W. P. 322 349 Jordan canonical form 108 Jump conditions 238 Jump phenomena 203 Juncosa, M. L. 44 83 89 90 91 124 132 159(41) 162 259(70) 314 Jury problem 5 Kahan, W. 129 162 Kalaba, R. 83 89 91 124 132 159(41) 162 259(70) 313 Kantorovich, L. V. 336 350 Kaplan, S. 2 39 50 51 91 200(19) 228 336 350 Kashara, A. 304 519 Kawarada, H. 340 350 Keller, H. B. 106 145 162 244 283 290 312 316 Kellogg, R. A. 125 164 Kennedy, J. F. 131 162 283(155) 317 Kerbel, J. 301(202) 318 Koch 322 349 Kolsky, H. 263 314 Kopal, Z. 328 349 Kreiss, H. 299 318 Kruskal, M. D. 265 315 Krylov, V. I. 336 350 Kulsrud, H. E. 125 164 Laasonen, P. 44 90 Ladyzhenskaya, O. A. 238 312 Laganelli, A. L. 74 77 79 91 Lagrangian difference equations 219 221 Lagrangian difference equations, implicit methods 221 Lagrangian difference equations, stability 220 Lagrangian equations 212 213 220 Lagrangian equations with pseudoviscosity 240 Lagrangian equations, advantages 239 Lagrangian equations, conservation form 219 221 243 Lagrangian equations, difference equations 220 221 Lagrangian mesh, distortion 263 Lakshmikantham, S. 339 350 Lanczos, C. 322 325 349 Landau, E. 11 40 Langhaar, H. L. 35 40 Laplace equation 23 92 Laplace equation, Dirichlet problem 95 116 Laplace equation, eigenvectors and eigenvalues 116 Laplace equation, five-point molecule SOR 126 Laplace equation, Gauss — Seidel method 114 Laplace equation, Jacobi method 114 Laplace equation, Neumann problem 96 Laplace equation, nine-point molecule 127 128 Laplace equation, simple finite difference schemes 94—97 Laplace equation, unequal mesh spacing 129 Laplace operator, five-point method 19 Laplace operator, nine-point method 19 Laplace operator, vector 296 Lavrentiev, M. M. 41 90 Lax — Wendroff method 217—220 241—243 Lax — Wendroff method, Eulerian equations 217—219 Lax — Wendroff method, stability 218 Lax — Wendroff method, staggered scheme 241 Lax, first-order method 222 Lax, P. D. 216 217 222 226(49) 228 241 242 243 263 265 312 315 Lazarus, R. B. 263 315 Le Roux, J. 1 Least squares method 322 Lee, S. Y. 37(61) 40 176(6) 202(6) 227 265(105) 315 Leela, S. 339 350 Lees, M. 72 82 85 91 157 200 201 228 255 313 Lelevier’s scheme (Eulerian gas equations) 215 Lelevier’s scheme (Eulerian gas equations), stability 215 Leone, F. C. 27 40 Levine, D. A. 244(29) 312 Lewy, H. 205(14) 228 Lieberstein, H. M. 236 256 258 311 313 Liebmann method, extended 256 Liebmann, H. 1 39 Liittschwager, J. 302 319 Line method 302—304 Line method for diffusion equation 303 304 Linear equations, direct method 98 Linear equations, iteration methods 98—100 Linear operator 334 Linear operator, positive 334 Linear operator, positive definite 334 Linear operator, symmetric 334 Linearization, Newton 83 89 Linearization, Picard 83 89 Liniger, W. 98(8) 161 Lipschitz condition 337 Liskovets, O. A. 302 319
Реклама
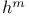extrapolation 
|
|
О проекте