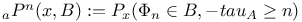|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Meyn S.P., Tweedie R.L. — Markov Chains and Stochastic Stability |
|
|
 |
| Предметный указатель |
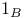 , indicator function of B 68 , indicator function of B 68
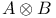 , Kronecker product 404 , Kronecker product 404
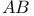 , uniformly accessibility 91 , uniformly accessibility 91
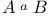 , uniformly accessibility using a 120 , uniformly accessibility using a 120
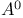 , points from which A is inaccessible 91 , points from which A is inaccessible 91
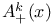 , states reachable from x at time k by CM(F) 150 , states reachable from x at time k by CM(F) 150
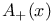 , states reachable from x by CM(F) 150 , states reachable from x by CM(F) 150
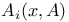 , ladder chain transition probabilities 77 , ladder chain transition probabilities 77
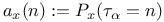 313 313
 , infinitely differentiable lunctions 29 , infinitely differentiable lunctions 29
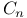 , controllability matrix 96 , controllability matrix 96
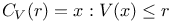 , sublevel set of V 190 , sublevel set of V 190
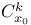 , generalized controllability matrix 155 , generalized controllability matrix 155
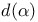 , period of , period of  114 114
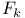 , output maps for LCM 30 , output maps for LCM 30
![$G_C^{(r)}(x,B)=E_x[\sum_{k=0}^{\sigma_C}1_B(\Phi_k)r^k]$](/math_tex/0f44b8aff7c145ceafe4fe95b08d192d82.gif) 367 367
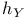 , almost everywhere invariant function 412 , almost everywhere invariant function 412
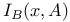 72 72
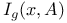 129 129
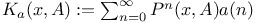 119 119
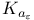 , resolvent kernel 68 , resolvent kernel 68
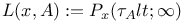 70 70
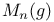 , martingale derived from g 434 , martingale derived from g 434
 , interpolation of , interpolation of 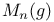 435 435
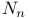 , customers in q. before , customers in q. before 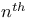 arrival 46 arrival 46
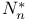 , customers in q. after , customers in q. after 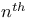 service time 48 service time 48
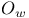 , control set 152 156 , control set 152 156
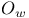 , supports disturbance/control in CM(F) or NSS(F) models 32 , supports disturbance/control in CM(F) or NSS(F) models 32
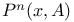 , n-step transition probability 59 67 , n-step transition probability 59 67
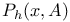 , Kernel for process on h 292 , Kernel for process on h 292
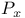 , probability conditional on , probability conditional on 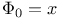 16 16
 200 200
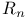 , residual service time 77 , residual service time 77
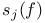 , sum of , sum of 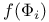 between visits to atom 417 between visits to atom 417
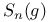 , partial sum of , partial sum of 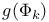 410 410
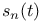 , interpolation of , interpolation of 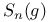 435 435
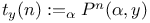 313 313
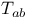 , coupling time 317 , coupling time 317
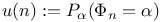 313 313
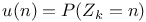 43 43
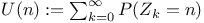 178 178
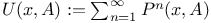 70 70
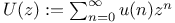 178 178
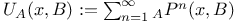 73 73
![$U_C^{(r)}(x,B)=E_x[\sum_{k=1}^{\tau_C}1_B(\Phi_k)r^k]$](/math_tex/b141dcd4fdd178f5b955d5f7ef787ff982.gif) 364 364
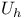 , resolvent kernel 290 , resolvent kernel 290
![$U_{\alpha}^{(r)}(x,f)=E_x[\sum_{n=1}^{\tau_{\alpha}}f(\Phi_n)r^n]$](/math_tex/c7dbd3b15c4441842d72ae276f33978f82.gif) 357 357
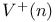 , forward recurrence time chain 44 , forward recurrence time chain 44
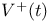 , forward recurrence time process 75 , forward recurrence time process 75
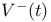 , backward recurrence process 75 , backward recurrence process 75
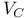 , minimal solution to (V2) 266 , minimal solution to (V2) 266
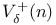 , forward recurrence , forward recurrence  -skeleton 75 -skeleton 75
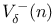 , backward recurrence , backward recurrence  -skeleton 75 -skeleton 75
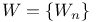 , increment process 24 , increment process 24
 , atom 100 , atom 100
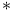 , convolution operator 74 , convolution operator 74
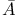 , points from which A is accessible 91 , points from which A is accessible 91
 , points reaching A in m steps 91 , points reaching A in m steps 91
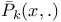 , Cesaro average of , Cesaro average of 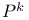 285 285
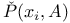 , the split transition lunction 103 , the split transition lunction 103
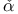 , the atom in , the atom in  104 104
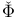 , the split chain 103 , the split chain 103
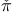 , split invariant measure 240 , split invariant measure 240
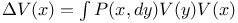 , drift operator 174 , drift operator 174
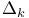 , derivative process 166 , derivative process 166
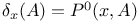 , Dirac measure 67 , Dirac measure 67
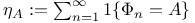 70 70
 , distribution of disturbance variable 24 , distribution of disturbance variable 24
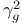 , limiting variance in the CLT 411 , limiting variance in the CLT 411
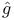 , solution to the Poisson equation 431 , solution to the Poisson equation 431
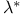 , split measure on , split measure on  103 103
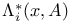 , zero-level l. c. transition probabilities 77 , zero-level l. c. transition probabilities 77
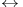 , communicates with 82 , communicates with 82
 , complex plane 140 , complex plane 140
 , real line 516 , real line 516
 , n-dimensional Euclidean space 6 , n-dimensional Euclidean space 6
 , integers 61 , integers 61
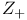 , non-negative integers 3 , non-negative integers 3
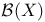 , ,  -field of subsets ol X 55 -field of subsets ol X 55
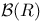 , Borel , Borel  -field on -field on  516 516
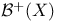 , sets with , sets with 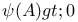 89 89
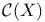 , continuous bounded lunctions on X 128 520 , continuous bounded lunctions on X 128 520
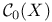 , continuous lunctions vanishing at , continuous lunctions vanishing at  523 523
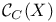 , continuous lunctions with compact support 143 , continuous lunctions with compact support 143
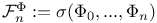 69 69
 72 72
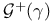 , distributions with Laplace — Stieltjes transform convergent in , distributions with Laplace — Stieltjes transform convergent in ![$[0,\gamma]$](/math_tex/0cb1bbf2f52cc776046a3683840febe482.gif) 389 389
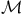 , space ol Borel probability measures 19 , space ol Borel probability measures 19
 , norm on , norm on 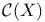 145 145
 385 385
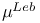 , Lebesgue measure on , Lebesgue measure on  93 516 93 516
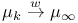 , Weak convergence 143 , Weak convergence 143
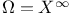 , sequence space 55 , sequence space 55
 , omega limit set for NSS(F) 157 , omega limit set for NSS(F) 157
 Markov chain 3 66 Markov chain 3 66
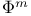 , the m-skeleton chain 68 , the m-skeleton chain 68
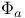 , sampled chain with transition kernel , sampled chain with transition kernel 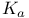 119 119
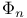 , Markov chain value at time n 3 , Markov chain value at time n 3
 , invariant measure 229 , invariant measure 229
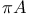 , invariant random variable 414 , invariant random variable 414
 , maximal irreducibility measure 88 , maximal irreducibility measure 88
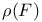 , maximum eigenvalue modulus 140 , maximum eigenvalue modulus 140
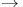 , leads to 82 , leads to 82
 -field 515 -field 515
 -field generated by r.v. 518 -field generated by r.v. 518
 -finite measure 516 -finite measure 516
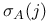 , , 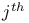 hitting time on A 417 hitting time on A 417
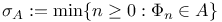 , hitting time on A 70 , hitting time on A 70
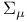 , ,  -field of -field of 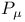 -invariant events 412 -invariant events 412
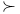 , absolute continuity 80 , absolute continuity 80
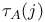 , , 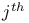 return time on A 70 return time on A 70
 , return time to A 16 70 , return time to A 16 70
 , disturbance, noise, innovation process 24 , disturbance, noise, innovation process 24
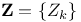 , discrete time renewal process 43 , discrete time renewal process 43
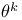 , , 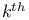 order shift operator on order shift operator on  69 69
 , irreducibility measure 87 , irreducibility measure 87
 -irreducibity 87 -irreducibity 87
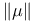 , total variation norm 311 , total variation norm 311
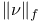 , f-norm 330 , f-norm 330
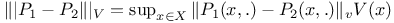 382 382
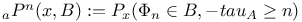 73 73
Absolute continuity 80
Absorbing set 89
Absorbing set, maximal a.s. 204
Accessible atom 100
Accessible set 91
Adaptive control 38
Adaptive control model, boundedness in probability 303
Adaptive control model, irreducibility 165
Adaptive control model, performance 406
Adaptive control model, simple 39
Adaptive control model, V-Uniform ergodicity 406
Age process 44
Antibody model 471
Aperiodic Ergodic Theorem 309
Aperiodicity 116 118
Aperiodicity, strong a. 116
Aperiodicity, topological a. for states 447
ARMA model 27 28
Ascoli’s Theorem 520
Assumptions for models, (AR1) 27
Assumptions for models, (AR2) 27
Assumptions for models, (ARMA1) 28
Assumptions for models, (ARMA2) 28
Assumptions for models, (CM1) 33
Assumptions for models, (CM2) 151
Assumptions for models, (CM3) 156
Assumptions for models, (CSM1) 52
Assumptions for models, (CSM2) 52
Assumptions for models, (DBL1) 36
| Assumptions for models, (DBL2) 36
Assumptions for models, (DS1) 260
Assumptions for models, (DS2) 260
Assumptions for models, (LCM1) 9
Assumptions for models, (LCM2) 9
Assumptions for models, (LCM3) 95
Assumptions for models, (LSS1) 9
Assumptions for models, (LSS2) 9
Assumptions for models, (LSS3) 97
Assumptions for models, (LSS4) 139
Assumptions for models, (LSS5) 140
Assumptions for models, (NARMA1) 33
Assumptions for models, (NARMA2) 33
Assumptions for models, (NSS1) 32
Assumptions for models, (NSS2) 32
Assumptions for models, (NSS3) 156
Assumptions for models, (Q1) 45
Assumptions for models, (Q2) 45
Assumptions for models, (Q3) 45
Assumptions for models, (Q4) 47
Assumptions for models, (Q5) 48
Assumptions for models, (RCA1) 404
Assumptions for models, (RCA2) 404
Assumptions for models, (RCA3) 404
Assumptions for models, (RT1) 44
Assumptions for models, (RT2) 44
Assumptions for models, (RT3) 75
Assumptions for models, (RT4) 75
Assumptions for models, (RW1) 11
Assumptions for models, (RW2) 111
Assumptions for models, (RWHL1) 14
Assumptions for models, (SAC1) 39
Assumptions for models, (SAC2) 39
Assumptions for models, (SAC3) 39
Assumptions for models, (SBL1) 30
Assumptions for models, (SBL2) 154
Assumptions for models, (SETAR1) 31
Assumptions for models, (SETAR2) 142
Assumptions for models, (SETAR3) 223
Assumptions for models, (SLM1) 25
Assumptions for models, (SLM2) 25
Assumptions for models, (SNSS1) 29
Assumptions for models, (SNSS2) 29
Assumptions for models, (SNSS3) 152
Assumptions for models, (SSM1) 49
Assumptions for models, (SSM2) 49
Assumptions for models, (V1) 190
Assumptions for models, (V2) 262
Assumptions for models, (V3) 337
Assumptions for models, (V4) 367
atom 100
Atom, Ergodic 314
Atom, f-Kendall a. 360
Atom, Geo. ergodic a. 357
Autoregression 27
Autoregression, dependent parameter random coeff. a. 36
Autoregression, random coefficient a. 404
Backward recurrence time  -skeleton 75 -skeleton 75
Backward recurrence time chain 44 60
Backward recurrence time process 75
Balayage operator 305
Bilinear model 30
Bilinear model, dependent parameter b.m. 36
Bilinear model, f-regularity and ergodicity for b.m. 347
Bilinear model, Geo. ergodicity for b.m. 380 403
Bilinear model, irreducible T-chains as b.m. 155
Bilinear model, multidimensional b.m. 403
Blackwell Renewal Theorem 348
Borel  -field 516 519 -field 516 519
Bounded in probability 145 301
Bounded in probability for T-chains 455
Bounded in probability on average 285
Brownian motion 525
Causality in control 38
Central limit theorem 411
Central Limit Theorem for Martingales 525
Central Limit Theorem, CLT for Autoregressions 442
Central Limit Theorem, CLT for Random walks 442
Central Limit Theorem, functional CLT 431 435
Chapman — Kolmogorov equations 67 68
Chapman — Kolmogorov equations, generalized C-K.e. 120
Closed sets 519
Closure of sets 519
Communication of discrete states 82
Compact set 519
Comparison theorem 337
Comparison Theorem, geometric C.T. 368
Conditional expectation 518
Continuous function 520
Control set 30 32 152 156
Controllability grammian 98
Controllability matrix 155
Controllable 16 95
Converges to infinity 201 207
Convolution 43 74 520
Countably generated  -field 516 -field 516
Coupling 316
Coupling time 317
Coupling to bound sums 325
Coupling, null chains 448
Coupling, renewal processes 316
Cruise control 3
Cyclic classes 115
Cyclic classes for control models 161
Cyclic classes, content-dependent release rules 50
Dams 48
Dense sets 519
Dependent parameter bilinear model 35
Dependent parameter bilinear model, Geo. ergodicity for the d.p.b.m. 479
Derivative process 166
Dirac probability measure 67
Disturbance 24
Doeblin’s condition 391 407
Dominated Convergence Theorem 518
Drift criteria 174 496 501
Drift criteria for deterministic models 259
Drift criteria for f-moments 331 337
Drift criteria for geometric ergodicity 367
Drift criteria for invariant measures 296
Drift criteria for non-evanescence 215
Drift criteria for non-positivity 276 499
Drift criteria for positivity (Foster’s criterion) 262 499
Drift criteria for positivity for e-chains 298
Drift criteria for recurrence 190
Drift criteria for recurrence, converse for Feller chains 215
Drift criteria for transience 189 276
Drift criteria, history dependent 474
Drift criteria, mixed 481
Drift criteria, state dependent 466
Drift operator 174
Dynamical system 19 28
Dynkin’s formula 263
e-chain 144
e-chain, aperiodicity for 458
Eigenvalue condition 140
Embedded Markov chains 7
Equicontinuous functions 520
Equicontinuous Markov chains (e-chains) 144
Ergodic atom 314
Ergodicity 312 500
Ergodicity for e-chains 459
Ergodicity for null chains 446
Ergodicity, f-e. 331
Ergodicity, f-geometric 355 374
Ergodicity, f-norm 330
Ergodicity, history of 329
Ergodicity, strong 407
Ergodicity, uniform 383 390
Ergodicity, V-uniform 382
Error 24
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



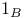 , indicator function of B
, indicator function of B 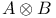 , Kronecker product
, Kronecker product 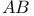 , uniformly accessibility
, uniformly accessibility 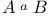 , uniformly accessibility using a
, uniformly accessibility using a 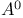 , points from which A is inaccessible
, points from which A is inaccessible 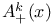 , states reachable from x at time k by CM(F)
, states reachable from x at time k by CM(F) 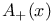 , states reachable from x by CM(F)
, states reachable from x by CM(F) 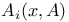 , ladder chain transition probabilities
, ladder chain transition probabilities 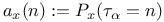
 , infinitely differentiable lunctions
, infinitely differentiable lunctions 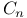 , controllability matrix
, controllability matrix 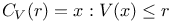 , sublevel set of V
, sublevel set of V 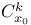 , generalized controllability matrix
, generalized controllability matrix 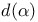 , period of
, period of 
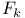 , output maps for LCM
, output maps for LCM ![$G_C^{(r)}(x,B)=E_x[\sum_{k=0}^{\sigma_C}1_B(\Phi_k)r^k]$](/math_tex/0f44b8aff7c145ceafe4fe95b08d192d82.gif)
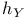 , almost everywhere invariant function
, almost everywhere invariant function 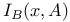
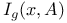
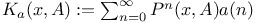
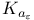 , resolvent kernel
, resolvent kernel 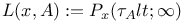
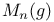 , martingale derived from g
, martingale derived from g  , interpolation of
, interpolation of 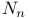 , customers in q. before
, customers in q. before 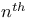 arrival
arrival 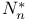 , customers in q. after
, customers in q. after 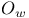 , control set
, control set 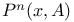 , n-step transition probability
, n-step transition probability 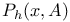 , Kernel for process on h
, Kernel for process on h 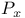 , probability conditional on
, probability conditional on 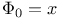

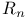 , residual service time
, residual service time 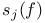 , sum of
, sum of 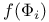 between visits to atom
between visits to atom 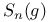 , partial sum of
, partial sum of 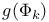
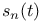 , interpolation of
, interpolation of 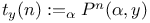
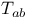 , coupling time
, coupling time 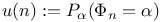
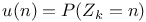
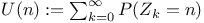
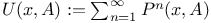
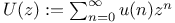
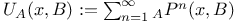
![$U_C^{(r)}(x,B)=E_x[\sum_{k=1}^{\tau_C}1_B(\Phi_k)r^k]$](/math_tex/b141dcd4fdd178f5b955d5f7ef787ff982.gif)
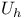 , resolvent kernel
, resolvent kernel ![$U_{\alpha}^{(r)}(x,f)=E_x[\sum_{n=1}^{\tau_{\alpha}}f(\Phi_n)r^n]$](/math_tex/c7dbd3b15c4441842d72ae276f33978f82.gif)
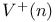 , forward recurrence time chain
, forward recurrence time chain 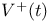 , forward recurrence time process
, forward recurrence time process 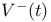 , backward recurrence process
, backward recurrence process 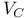 , minimal solution to (V2)
, minimal solution to (V2) 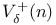 , forward recurrence
, forward recurrence  -skeleton
-skeleton 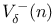 , backward recurrence
, backward recurrence 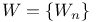 , increment process
, increment process 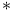 , convolution operator
, convolution operator 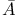 , points from which A is accessible
, points from which A is accessible  , points reaching A in m steps
, points reaching A in m steps 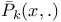 , Cesaro average of
, Cesaro average of 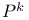
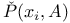 , the split transition lunction
, the split transition lunction 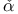 , the atom in
, the atom in 
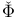 , the split chain
, the split chain 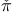 , split invariant measure
, split invariant measure 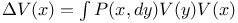 , drift operator
, drift operator 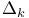 , derivative process
, derivative process 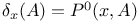 , Dirac measure
, Dirac measure 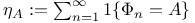
 , distribution of disturbance variable
, distribution of disturbance variable 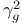 , limiting variance in the CLT
, limiting variance in the CLT 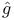 , solution to the Poisson equation
, solution to the Poisson equation 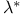 , split measure on
, split measure on 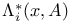 , zero-level l. c. transition probabilities
, zero-level l. c. transition probabilities 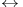 , communicates with
, communicates with  , complex plane
, complex plane  , real line
, real line  , n-dimensional Euclidean space
, n-dimensional Euclidean space  , integers
, integers 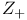 , non-negative integers
, non-negative integers 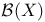 ,
,  -field of subsets ol X
-field of subsets ol X 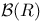 , Borel
, Borel 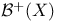 , sets with
, sets with 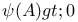
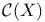 , continuous bounded lunctions on X
, continuous bounded lunctions on X 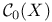 , continuous lunctions vanishing at
, continuous lunctions vanishing at 
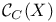 , continuous lunctions with compact support
, continuous lunctions with compact support 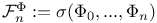

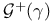 , distributions with Laplace — Stieltjes transform convergent in
, distributions with Laplace — Stieltjes transform convergent in ![$[0,\gamma]$](/math_tex/0cb1bbf2f52cc776046a3683840febe482.gif)
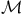 , space ol Borel probability measures
, space ol Borel probability measures  , norm on
, norm on 
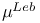 , Lebesgue measure on
, Lebesgue measure on 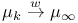 , Weak convergence
, Weak convergence 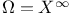 , sequence space
, sequence space  , omega limit set for NSS(F)
, omega limit set for NSS(F)  Markov chain
Markov chain 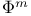 , the m-skeleton chain
, the m-skeleton chain 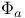 , sampled chain with transition kernel
, sampled chain with transition kernel 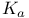
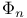 , Markov chain value at time n
, Markov chain value at time n  , invariant measure
, invariant measure 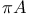 , invariant random variable
, invariant random variable  , maximal irreducibility measure
, maximal irreducibility measure 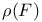 , maximum eigenvalue modulus
, maximum eigenvalue modulus 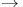 , leads to
, leads to 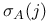 ,
, 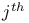 hitting time on A
hitting time on A 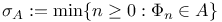 , hitting time on A
, hitting time on A 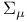 ,
, 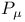 -invariant events
-invariant events 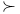 , absolute continuity
, absolute continuity 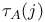 ,
,  , return time to A
, return time to A  , disturbance, noise, innovation process
, disturbance, noise, innovation process 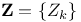 , discrete time renewal process
, discrete time renewal process 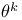 ,
, 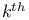 order shift operator on
order shift operator on 
 , irreducibility measure
, irreducibility measure 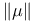 , total variation norm
, total variation norm 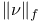 , f-norm
, f-norm