|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Meyn S.P., Tweedie R.L. — Markov Chains and Stochastic Stability |
|
|
 |
| Предметный указатель |
Evanescence 17 207
Evanescence for Feller chains 457
Exchange rate 4
Exogenous variables 37
Expectation 518
f-regularity 332 352
f-regularity, criterion for 338
f-total variation norm 330
Fatou’s Lemma 517
Feller property 128
Finiteness of moments 345
First entrance decomposition 176 180
First-entrance last-exit decomposition 312
Forward accessible 151 155
Forward recurrence time chains 44 60 236
Forward recurrence time chains,  -skeleton 75 112 349 -skeleton 75 112 349
Forward recurrence time chains, Geo. ergodicity for 361
Forward recurrence time chains, positivity for 247
Forward recurrence time chains, recurrence for 177
Forward recurrence time chains, regularity for 271
Forward recurrence time chains, V-uniform ergodicity for 389
Forward recurrence time process 75
Foster — Lyapunov criteria 19
Foster’s criterion 262 284
Full set 89
Functional CLT 525
Functions unbounded off petite sets 191
Generalized sampling 289
Geometric Ergodic Theorem 354
Geometric ergodicity 354 360
Geometric ergodicity, drift criterion for 367
Geometrically ergodic atom 357 360
Globally attracting 160
Gumleaf attractor 34
Harmonic functions 414
Harris  -property 497 -property 497
Harris recurrence 200
Harris recurrence, topological of states 209
Harris, maximal set 205
Harris, positive 231
Increment (or disturbance) 24
Increment analysis 219
Increment analysis, geometric 397
Indecomposable 159
Independent and identically distributed 9
Indicator function 68 516
Inessential sets 199
Initial condition 55
Initial distribution 57
Innovation 24
Integrable functions 517
Invariant  -fields 412 -fields 412
Invariant events 414
Invariant measures 229
Invariant measures for e-chains 297
Invariant measures for Feller chains 287 295
Invariant measures for recurrent chains 241
Invariant measures, structure of 245
Invariant random variables 412 414
Invariant set 157
Invasion/antibody model 471
Irreducibity 83
Irreducibity, maximal measure 89
Irreducibity, open set 131 133
J, interarrival times for a dam 49 52
Kac’s Theorem 236
Kaplan’s condition 491
Kendall sets 364
Kendall’s Theorem 358
Kernel 65
Kernel, n-step transition probability 67
Kernel, Substochastic 77
Kernel, Transition probability 65
Kolmogorov’s inequality 524
L(x, h) 292
Ladder chains 76
Ladder chains, positivity for 248
Last-exit decomposition 180
Law of Large Numbers 410 413
Law of large numbers for e-chains 461
Law of large numbers, ratio form of the 417 424
Law of the iterated logarithm 411
LCM(F,G) model 9
Lebesgue integral 516
Lebesgue measure 516
Lindelof’s theorem 519
Linear control model 8 9 95
Linear control model, controllability for the 96
Linear state space models 9
Linear state space models as T-chains 138
Linear state space models, boundedness in prob. for 301
Linear state space models, central Limit Theorem for 443
Linear state space models, Gaussian 97 114
Linear state space models, positivity for 251
Linear state space models, simple 25
Linked forward recurrence time chains 237
Locally compact 519
Lower semicontinuous 126 520
M-irreducibity 160
Markov chain 3 58 66
Markov chain, definition of 55
Markov chain, time-homogeneous 58
Markov property 69
Markov property, strong 72
Markov transition function 65
Markov transition matrix 59
Martingale 524
Martingale difference sequence 524
Maximal Harris set 205
Maximal irreducibility measure 89
Mean drift 225
Mean square stabilizing 38
Measurable function 516
Measurable space 515
Measure 516
Metric space 519
Minimal set 158
Minimal subinvariant measures 243
Minimum variance control 38
Minorization Condition 102
Mixing 408
Mixing, V-geometric mixing 387
moment 228
Monotone Convergence Theorem 517
Moran dam 49 74
Multidimensional models 469
N(t), customers in queue at time t 45
Neighborhoods 519
networks 5 284
Noise 24
Non-evanescent 207 286 498
Nonlinear state space model 29 130 149
Nonlinear state space model, associated control system for 33
Nonlinear state space model, V-uniform ergodicity and 396
Norm, f 330
Norm, operator V-norm 385
Norm, total variation 310
Norm, V-norm 382
Norm-like functions 214 522
Norm-like sequence 476
NSS(F) model 32
Null chains 498
Null chains, 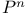 -definition 498 500 -definition 498 500
Null chains,  -definition 499 -definition 499
Null Markov process 230
Null sets 454
Null states 453 456
Occupation probabilities 461
Occupation time 70
Open sets 519
| Orey’s Theorem 451
p(M), upper tail of renewal sequence 448
p(n), increment distribution of renewal sequence 43
P(x, A), one-step transition probability 58 66
Pakes’ lemma 283
Period 118
Persistence 199
Petite set 121
Phase-type service times 402
Poisson equation 431
Polling systems 401
Populations 5
Positive chain 230 498
Positive chain, 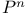 -definition 498 500 -definition 498 500
Positive chain,  -definition 499 -definition 499
Positive chain, T-chains 455
Positive sets 454
Positive state 447 453
Positive state, topologically 446
Precompact sets 519
Probability space 518
Process on A 244 253 294
Q(x, h) 292
Quasi-compact 407
Queues 4 45
Queues with re-entry 272
Queues, Geo. ergodicity for M/G/1 401
Queues, GI/G/1 47 76 111
Queues, GI/M/1 47 62 239
Queues, GI/M/1, positivity of the GI/M/1 240
Queues, GI/M/1, transience of the GI/M/1. 197
Queues, M/G/1 48 86
Queues, M/PH/1 402
Queues, phase type service and geo. ergodicity 402
Queues, polling systems and geo. ergodicity 401
Queues, positivity for M/G/1 237
Queues, Positivity for the GI/G/1 248 488
Q{A}, invariant random variable 414
R(x), emptying time for dam 51
Random coefficient autoregression 404
Random variable 518
Random walk 11 61 93 247
Random walk on half line 14 73 81 195 220
Random walk on half line, Bernoulli 178
Random walk on half line, Bernoulli, Geo. ergodicity of 379
Random walk, Central Limit Theorem for 442
Random walk, continuous components for 137
Random walk, f-regularity and ergodicity for 346
Random walk, recurrent 192
Random walk, regularity of 270
Random walk, simple 178
Random walk, transient 193
Random walk, V-uniform ergodicity of 389
Randomized first entrance times 289
Rate of convergence, exact 392
Rate of convergence, geometric 354
Ratio limit theorem 417
Reachable state 131 133 447 455
Real line 516
Recurrence 17
Recurrence, 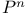 -definition 496 -definition 496
Recurrence,  -definition 497 -definition 497
Recurrence, deterministic systems 260
Recurrent atom 175
Recurrent chain 176 182 496
Recurrent chain, structure of  for 245 for 245
Recurrent set 173
Recurrent state 211
Regeneration times 43 105
Regenerative decomposition 320 356
Regenerative decomposition for geometrically regular chains 356
Regularity 255 333 498
Regularity and ergodicity 328
Regularity for Markov chains 498
Regularity for measures 519
Regularity for sets 255
Regularity for sets, f-geometrically regular sets 364
Regularity for sets, f-regular sets 333 339
Regularity, criterion for f-geometric regularity 367
Regularity, f-geometric 364 371
Renewal measure 75
Renewal process 43
Renewal process, delayed 74
Renewal process, recurrence for 177
Renewal Theorem 347
Renewal Theorem, Blackwell’s 348
Renewal Theorem, Kendall’s 358
Residual lifetime process 44
Resolvent equation 291
Resolvent kernel 68
Running maximum 425
Sample paths 55
Sampled chain 119
Sampled chain, generalized 289
Sampling distribution 119
Sampling, generalized 289
Semi-dynamical system 19 260
Separability 519
Sequence or path space 55
SETAR model 31 142 503
SETAR model, null recurrence 277
SETAR model, regularity 274
SETAR model, transience 222
Shift operator 69
Simple linear model 25
Simple linear model, regularity for the 271
Skeleton 68
Skip-free chain, invariant measure for 238
Skip-free random walk on a half line 197
Skip-free to the left, g 399
Skip-free to the right 77
Small set 106
SNSS(F) model 29
Splitting 102
Splitting a general Harris chains 422
Spread-out 111 247
Stability 15 173
Stability in the sense of Lyapunov 20
Stability, 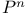 -properties and 496 -properties and 496
Stability,  -properties and 496 -properties and 496
Stability, asymptotic 20
Stability, Drift properties and 496
Stability, global asymptotic 20
Stability, global exponential 302
Stability, Lagrange 20
Stability, Lagrange, for CM(F) model 396
State spaces 56
Stationary processes 230
Stochastic comparison 219
Stopping times 71
Stopping times, first hitting 70
Stopping times, first return 70
Storage model 4
Storage model, content-dependent 52
Storage model, simple 49 62
Strong Feller property 128
Strong Markov property 72
Strong mixing 383 387
Subinvariant measures 232
Sublevel set 190 520
Supermartingale 524
T(x,A), continuous component 127
T-chain 127 133
T-chain, bounded in probability 455
T-chain, positive recurrent 455
Taboo probabilities 73
Test function 501
Test set 501
The Martingale Convergence Theorem 524
Tight 17 285 521
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -skeleton
-skeleton  -property
-property  -fields
-fields  -definition
-definition  for
for