|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Pollard D. — Convergence of Stochastic Processes |
|
|
 |
| Предметный указатель |
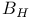 See “Brownian motion stretched See “Brownian motion stretched
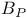 See “P-motion” See “P-motion”
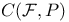 156 156
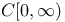 108 108
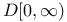 , definition of 107 , definition of 107
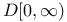 , metric of uniform convergence on compacta 108 , metric of uniform convergence on compacta 108
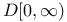 , Skorohod metric 123 , Skorohod metric 123
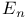 See “Empirical process” See “Empirical process”
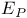 See “P-bridge” See “P-bridge”
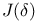 xiv (See also “Covering integral”) xiv (See also “Covering integral”)
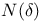 xiv (See also “Covering number”) xiv (See also “Covering number”) 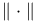
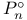 15 26 149 15 26 149
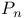 See “Empirical measure” See “Empirical measure”
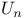 See “Empirical process uniform” See “Empirical process uniform”
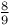 -argument 24 -argument 24
 156 156
 See “Projection See “Projection  -field” -field”
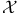 See “Function space” See “Function space”
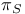 See “Projection maps” See “Projection maps”
 xiv xiv
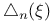 21 21
2-means See “k-means”
Abuse, of notation 44 171
Adapted 176
Aldous, D. 133 137 185 187
Aldous’s condition 133
Alexander, K. S. 38 166
Alexandroff, A. D. 85
Allocation Lemma 77
Almost-sure representation See “Representation Theorem”
Amato, B. R. viii
Approximation Lemma 27
Araujo, A. 37
Ash, R. B. 39
Autoregression 12 174
Axiom of Choice 65 86
Barry, D. G. viii
Bennett, G. 193—194
Bennett’s Inequality 160 192 194
Bernstein’s inequality 193
Bertrand-Retali, M. 38 41
Bias, of density estimator 35 42
Billingsley, P. 36 61 85—86 117—118 136
Binomial coefficient 19
Bollobas, B. 86
Bolthausen, E. 167
Bounded variation 42
Boyce, J. S. viii
Breiman, L. 4 22 106 118
Bremaud, P. 186
Breslow, N. 186
Brown, B. M. 166 185
Brownian bridge 64
Brownian bridge, denned 3 95
Brownian bridge, existence 101 119
Brownian motion, construction from brownian bridge 103
Brownian motion, defined 95
Brownian motion, modulus of continuity for 146
Brownian motion, stretched-out 178
Brownian motion, tied-down 3
Cadlag 3 89 176
Cauchy sequence 81
Censored data, estimation from 182
Central limit theorem, autoregression 174
Central Limit Theorem, Empirical for distribution functions 97
Central limit theorem, empirical process 157
Central Limit Theorem, Empirical, uniform case 96
Central Limit Theorem, Liapounoff 51
Central Limit Theorem, Lindeberg 52
Central limit theorem, martingale-difference array 171
Central limit theorem, minimization functional 141
Central Limit Theorem, Multivariate 57
Cervonenkis, A. Ya. 37
Chaining 37
Chaining for stochastic processes 142—145
Chaining Lemma 144
Chaining, restricted 160—163
Characteristic function 54
Characteristic function, Continuity Theorem 55 60
Characteristic function, inversion formula 63
Characteristic function, uniform convergence on compacta 59
Characteristic function, uniquely determines distribution 55
Chernoff, H. 165 190
Chi-square, Pearson’s 46
Chibisov, D. M. 85
Chung, K. L. 117
Clustering See “k-means”
Combinatorial method 13
Compactness in metric spaces 81—82
Compactness Theorem 82
Compactness, sequential 82
Completely regular, point of metric space 67
Completely regular, topological space 68
Conditional variance of increment 171
Conditional variance, process 176
Consistency for autoregression 12
Consistency of k-means 9
Consistency of optimal solutions 12
Continuity set 71
Continuity Theorem, for characteristic functions 55 60
Continuous Mapping Theorem for euclidean space 46
Continuous Mapping Theorem for metric spaces 70
Continuous Mapping Theorem, failure of 66
Convergence in distribution in euclidean space 43
Convergence in distribution of empirical process 97 157
Convergence in distribution of L2 martingale 179
Convergence in distribution, Aldous’s condition for, in 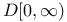 134 134
Convergence in distribution, in 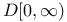 , for Skorohod metric 131 , for Skorohod metric 131
Convergence in distribution, in 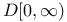 , for uniform convergence on compacta 108 , for uniform convergence on compacta 108
Convergence in distribution, in metric spaces 65
Convergence in distribution, of uniform empirical process 96
Convergence in distribution, process with independent increments 104 135
Convergence in distribution, via semicontinuity 73
Convergence in distribution, via uniform approximation 70
Convergence Lemma for euclidean space 44—46
Convergence Lemma for metric spaces 68
Convex sets, shattering 17 23
Convolution 35 49 54
Coupling 76—80
Coupling in Compactness Theorem 84
Covering integral as modulus of continuity 147
Covering integral for metric space 143
Covering numbers, 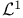 for classes of functions 25 for classes of functions 25
Covering numbers, 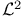 for classes of functions 31 for classes of functions 31
Covering numbers, direct 164
Covering numbers, for metric spaces 143
Covering numbers, for polynomial classes 27
Covering numbers, inequalities between 34
Covering numbers, measurability of 198
Covering numbers, random 150
Criterion function, minimization of 28
Criterion function, random 12
Cross-section, measurable 197
Crossword puzzle 76
Crowley, J. 186
C[0, 1] 1 90
DeHardt, J. 36
Dellacherie, C. 176 179 185 195—197
Delta method 63 189
Denby, L. 37
Density, convolution 55
Density, estimation 35
Differentiability, in quadratic mean 140 151
Direct approximation 8 164
Discrimination, linear; polynomial; quadratic 17
Distribution function, pointwise convergence of 43 46 53
Donsker, M. D. 117—118
Donsker’s theorem See “Central Limit Theorem Empirical”
Doob — Meyer decomposition 176
Doob, J. L. 3 117
| Dudley, R. M. vii 37—39 85—86 117—118 166—168 193 200
Durbin, J. 118
Durst, M. 39
D[0, 1] 3 89—90
Eggleston, H. G. 200
Empirical measure, bivariate 12
Empirical measure, defined 6
Empirical process, central limit theorem for 96—97
Empirical process, defined 2 95 97 140
Empirical process, measurability of 65 199
Envelope, for classes of functions 24 151
Equicontinuity Lemma 150
Equicontinuity of class of functions 74
Equicontinuity, stochastic 139
Erdos, P. 118
Ergodicity 9 12
Exponential bound See “Tail probability”
Exponential Bounds 16
Extreme-value distribution 128
Feller, W. 53 63 193
Fidi projection 92 (See also “Projection maps”)
Fidis (finite-dimensional distributions) 3 90 92
Function space 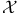 155 199 155 199
Functional in function space 156
Functional, first passage time 109 124
Functional, jump 179
Functional, terminology 2 7
Functions, infinitely differentiable 49
Gaenssler, P. vii 36—37 40 118 167
Gaussian process, characterization 106
Gaussian process, indexed by functions 146
Gihman, I.I. 4 117—118 136—137 166 185
Gill, R. D. 186
Gine, E. 37 40 166—167
Glaisher, J. W. L. 61
Glivenko — Cantelli theorem, classical 6—7 13
Glivenko — Cantelli theorem, generalized, for classes of functions 25
Glivenko — Cantelli theorem, generalized, for classes of sets 18 22
Gnedenko, B. V. 37
Goodness-of-fit statistic 2
Goodness-of-fit statistic with estimated parameters 99 159
Goodness-of-fit statistic, Kolmogorov’s, limiting distribution of 113
Goodness-of-fit statistic, Neyman’s 47
Graph, of real-valued function 27
Grid, approximations constructed from 91 124
Hajek, J. 86 117
Hall, P. 185
Halmos, P. R. 39
Hansel, G. 86
Hartigan, J. A. viii 36 166
Heuristic argument, Doob’s 4 64
Hewitt — Savage, zero-one law of 22
Heyde, C. C. 185
Hoeffding, W. 193—194
Hoeffding’s Inequality 16 26 31 150 164 191
Huber, P. J. 38 165 168
Independent increments, convergence in distribution 104 135
Independent increments, definition 103
Innovations 174
Integration 16
Interpolation in 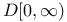 124 124
Interpolation in a function space 158
Interpolation in D[0, 1] 92
Interpolation, continuous 101
Jacobs, K. 86
Jacobsen, M. 186
k-means, central limit theorem 153
k-means, consistency 9 30
k-means, method of 9
Kac, M. 117—118
Kaplan — Meier estimator 182
Kelley, J. L. 39
Kernel, smoothing 35
Kernel, translates of 42
Kildea, D. G. 166
Kolchinsky, V. I. 38 166
Kolmogorov, A. N. 99 117 136 166
Kurtz, T. G. 137
Laplace transform, for hitting time 112
Le Cam, L. 37—38 85 166—167 200
Levy, P. 61
Liapounoff condition 51
Liapounoff, A. M. 61 63
Lindeberg condition 52 106
Lindeberg condition for martingale-difference arrays 171
Lindeberg, J. W. 61
Lindelof’s theorem 68 72 87
Lindvall, T. 118
Lipschitz condition 45 74 101
Liptser, R. S. 185
Little links 163
Location, center of 28
Loeve, M. 118
M-estimator, generalized 12
M-estimator, stochastic equicontinuity 165
Major, P. 86
Mann, H. B. 189
Marginal stacks, with coupling 77
Maritz, J. S. 166
Markov property for empirical process 96
Marriage lemma 77
Martin, R. D. 37
Martingale,  176 176
Martingale,  , convergence to gaussian process 179 , convergence to gaussian process 179
Martingale, continuous time 176
Martingale, difference array 171
Martingale, reversed 39
Martingale, reversed, empirical measure as 22
Martingale, stopped 180
Maximal inequality 15
Maximal inequality by chaining 144
Maximal inequality for  -martingales 177 -martingales 177
Maximal inequality for cadlag processes 94
Maximum likelihood 138
McKean, H. P. 146
McLeish, D. L. 185
Measurability, for random elements of metric spaces 64—66
Median, central limit theorem for 53 98
Median, consistency 7
Median, spatial, central limit theorem for 152
Median, spatial, consistency of 28
Metivier, M. 185
Metric, bounded-Lipschitz 74
Metric, entropy 166
Metric, Prohorov 75 79 88
Metric, Skorohod, on 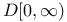 123—124 123—124
Meyer, P-A. 176 179 185 195—197
Minimization of random criterion function 140
Modulus function for 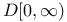 125 125
Multinomial distribution 46
Neveu, J. 22
Neyman, J. 47
Nolan, D. A. viii
Norm 14 24 156
Normal distribution, characteristic function of 63
Normal distribution, multivariate 29
Normal distribution, tail probabilities 191
Optimal centers 10
Outer measure 70
Oxtoby, J. C. 65 86
P-bridge 149
P-motion 147
Parr, W. 118
Parthasarathy, K. R. 85 136
Partial sum process 106 109
Permissible, classes of functions 24
Permissible, classes of sets 17
Permissible, definition 196
Philipp, W. 166 200
Pickands, J. 136
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



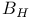
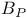
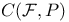
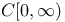
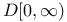 , definition of
, definition of 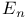
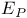
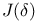
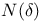
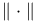
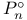
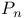
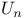
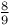 -argument
-argument 

 -field”
-field”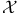
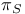

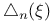
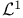 for classes of functions
for classes of functions 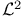 for classes of functions
for classes of functions 