|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Pollard D. — Convergence of Stochastic Processes |
|
|
 |
| Предметный указатель |
Poisson process 105 129
Pollard, D. 36—39 118 166 169
Polynomial, bound for number of sets picked out 19
Polynomial, class 17 27
Polynomial, discriminating 17
Polynomial, discrimination 17 20
Polynomial, orthogonal 47
Predictable 176
Product  -field 69 -field 69
Prohorov, Yu. V. 85-.86
Prohorov’s theorem See “Compactness Theorem”
Projection  -field 66 90 -field 66 90
Projection  -field on -field on 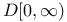 127 127
Projection  -field on D[0,1] 87 -field on D[0,1] 87
Projection maps 66 90
Projection maps for 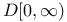 130 130
Projection, measurability of 196
Pyke, R. vii 85—86 167
Quadratic variation process 185
Quantile transformation 57 97 129
Random element of metric space 1 65
Random vector, characteristic functions 56
Random vector, convergence in distribution of 43 56
Random vector, perturbation of 48
Ranga Rao, R. 86
Rates of convergence 30
Reflection principle, for brownian motion 112
Remainder term in Taylor expansion 50 139
Representation Theorem with random elements 71
Representation Theorem with random variables 58
Resnick, S. I. 136
Revesz, P. 118 167
Robustnik 75
Sample path 1
Sauer, N. 37
Scheffe’s lemma 61
Semicontinuity 73 87
Seminorm xiv
Separability and  -fields 85 -fields 85
Separability for subsets of metric spaces 67
Separability of 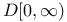 , under Skorohod metric 127 , under Skorohod metric 127
Separability of C[0,1] 87
Separability, universal 38
Shatter 18 21 198
Shelah, S. 37
Shiryayev, A. N. 185
Shorack, G. vii—viii 85
Sigma field See “
Sigma field, generated by balls 87
Sign variables 15
Signed measure See “ ” ”
Silverman, B. W. 38
Simmons, G. F. 67—68 85
Skorohod, A. V. 4 86 117—118 122 136—137 166 185
Slutsky’s theorem 62
Souslin 196
Square-root trick 32 37
Steele, J. M. 37
Stirling’s approximation 21
| Stochastic equicontinuity 139—140
Stochastic order symbol 141 189
Stochastic process 1
Stone, C. 118 136
Stopping time 110 172
Straf, M. 136
Strasbourg theory 176
Strassen, V. 86 167
Strong markov property, for brownian motion 111
Stute, W. vii 36—38 117
Submartingale 178
Submartingale, reversed 22 25
Subsets, hidden 19
Subsets, picked out 18
Substitution, of increments 49
Sun, T. G. 167
Symmetrization 32 149
Symmetrization Lemma 14 198
Symmetrization, First 14
Symmetrization, inequality 14—15
Symmetrization, Second 15
Symmetry and empirical measures 21
Tail probability, characteristic function bound 60
Tail probability, exponential bound 160
Tail probability, tied-down brownian motion See “Brownian bridge”
Talagrand, M. 85
Tight measure on metric space 81
Tight measure on real line 60
Tong, Y. L. 41
Topsoe, F. 36—37 62 85—86
Total boundedness and P-motion 168
Total boundedness of metric space 82
Triangular array 51 106
Troallic, J. P. 86
Truncation 25
Uniform convergence of density estimator 36
Uniform integrability 176
Uniform strong law of large numbers 7
Uniform strong law of large numbers for classes of functions 25 168
Uniform strong law of large numbers for classes of sets 18 22
Uniform strong law of large numbers for convex sets 22
Uniform tightness for general empirical processes 156
Uniform tightness for uniform empirical processes 102
Uspensky, J. V. 61 193
Usual conditions 176
Vapnik, V. N. 37
Varadarajan, V. S. 85
VC class 37
Vector space, finite-dimensional 20 30 38
Wald, A. 189
Weak convergence in euclidean space 44
Weak convergence in metric spaces 65
Weierstrass, K. 61
Weight functions 158
Wellner, J. viii
Whitt,W. 118
Wichura, M. 86
Yu, K. F. 186
Zinn, J. 37 38 40 166—167
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -field
-field 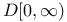

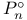 ”
”