јвторизаци€
ѕоиск по указател€м
Ash R.B. Ч Real Variables with Basic Metric Space Topology
ќбсудите книгу на научном форуме Ќашли опечатку?
Ќазвание: Real Variables with Basic Metric Space Topologyјвтор: Ash R.B. јннотаци€: This is a text for a first course in real variables. The subject matter is fundamental for more advanced mathematical work, specifically in the areas of complex variables, measure theory, differential equations, functional analysis, and probability. In addition, many students of engineering, physics, and economics find that they need to know real analysis in order to cope with the professional literature in their fields. Standard mathematical writing, with its emphasis on formalism and abstraction, tends to create barriers to learning and focus on minor technical details at the expense of intuition. On the other hand, a certain amount of abstraction is unavoidable if one is to give a sound and coherent presentation. This book attempts to strike a balance that will reach the widest audience possible without sacrificing precision.
язык: –убрика: ћатематика /—татус предметного указател€: √отов указатель с номерами страниц ed2k: ed2k stats √од издани€: 2007 оличество страниц: 213ƒобавлена в каталог: 28.03.2010ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
ѕредметный указатель
"And" connective 15 "Implies" connective 15Ч16 "Not" connective 15 "Or" connective 15 148 148 Abel's theorem 55 Algebra of functions 137 Applications: of compactness 33Ч37 Applications: of the Mean Value Theorem 86Ч91 Applications: of the Weierstrass M-test 125Ч129 Arzela Ч Ascoli theorem 132Ч133 Bake Category Theorem 144Ч149 Bake Category Theorem, proof of 145Ч146 Ball 11 Bolzano Ч Weierstrass theorem 34Ч35 Bolzano Ч Weierstrass Theorem, corollary 35Ч36 Boundary point 23 42 Bounded function 65 125 Bounded sequence 34 Bounded sets 29Ч35 161Ч162 Bounded variation, functions of 106Ч111 Calculus, Fundamental Theorem of 104Ч105 Cantor diagonal process 8 Cantor set 76Ч80 Cantor's Nested, Set Property 29 164Ч165 Category 1 and category 2 145 Cauchy product of power series 139 Cauchy sequence 24 40Ч41 124 164 Cauchy Ч Schwarz inequality 52 Cauchy Ч Schwarz inequality, for integrals 115 Cauchy Ч Schwarz inequality, for sums 52 Chain rule 81Ч82 Change of variable formula 112 Closed ball 12 Closed sets 12Ч13 Closed sets, continuity and 61Ч62 Closed sets, relation between open sets and 13Ч14 Closed sets, unions and intersection of 25Ч28 Closure 22 Cluster point 21 Co-finite set 23 Codomain 57 Compact set 30 Compactness 28Ч37 161Ч164 Compactness, and closed, bounded sets 30 Compactness, and continuity 64Ч70 Compactness, applications of 33Ч37 Compactness, Bolzano Ч Weierstrass Theorem 34Ч35 Compactness, criteria for 162 Compactness, definition 30 Compactness, Heine Ч Borel Theorem 31Ч32 35 130 164 Compactness, nested set property 29 Complement 2 3 6 Complete metric space 41 Completeness, and least upper bounds 37Ч42 Composition of functions 59 Connectedness 150Ч152 Continuity 57Ч80 Continuity, and compactness 64Ч70 Continuity, definition 57 Continuity, discontinuities, types of 70Ч76 Continuity, epsilon-delta approach 57Ч58 Continuity, global vs. local concept of 59 67 Continuity, semicontinuous functions 152Ч158 Continuity, uniform 66Ч70 Continuous functions 57ff Contradiction, proof by 16Ч17 Contrapositive 17 Convergence see also УPointwise convergence; Uniform convergenceФ 10Ч15 Convergence pointwise 117Ч120 Convergence, of power series 52Ч55 Convergence, radius of 54 Convergent subsequence 33Ч34 Countable sets 7Ч10 Countably infinite sets 7Ч10 De Morgan laws 5 6 27 Decreasing function 74 85 Decreasing sequence 41 Deleted open ball 21 Dense set 68Ч69 145Ч146 Derivative 81ff Diagonal process 8 46 131 163 Differentiable function 81ff Differentiation 81Ч92 Differentiation, definition 81Ч83 Differentiation, Generalized Mean Value Theorem 85Ч86 Differentiation, Mean Value Theorem 83Ч85 Differentiation, Mean Value Theorem, applications of 86Ч91 Dini's theorem 124Ч125 Direct image 62Ч63 Disconnected sets 150Ч151 Discontinuities, infinite 71 Discontinuities, jump 71 Discontinuities, nonsimple 73 Discontinuities, of the first kind 71Ч72 Discontinuities, of the second kind 73Ч74 Discontinuities, point 71 Discontinuities, removable 71 Discontinuities, simple 71 Discontinuities, types of 70Ч76 Disjoint sets 5Ч6 151 Distance 10Ч15 Distance function 10 Distance, from a point to a set 79 Distributive law for sets 2 Domain 57 Empty set 5 Epsilon-delta characterization 57Ч58 71 73 76 Equicontinuity, and Arzela Ч Ascoli Theorem 130Ч133 Equicontinuous family of functions 131 Euclidean metric 10 52 Euclidean p-space 11 Euclidean plane 2 Eventually (ev) 49 Everywhere continuous, nowhere differentiable function 126Ч129 Existential quantifier 18 Extended real numbers 35 Extension: of a bounced continuous function 143 Extension: of a uniformly continuous function 69 Extension: Tietze Extension Theorem 143 Finite sets 7 Function 33 Function, bounded 65 125 Function, continuous 57ff Function, decreasing 74 85 Function, differentiable 81ff Function, everywhere continuous and nowhere differentiable 126Ч129 Function, increasing 74 85 Function, left-continuous 111 Function, lower semicontinuous 152 Function, monotone 74 Function, of bounded variation 106Ч111 Function, right-continuous 110 Function, semicontinuous 152Ч158 Function, uniformly continuous 66Ч70 Function, upper semicontinuous 152 Function, variation of a 106 Fundamental theorem of calculus 104Ч105 Fundamental Theorem of Calculus, intuitive view of 105 Generalized Mean Value Theorem 85Ч86 Global concept of continuity 59 67 Greatest lower bound 38 Heine Ч Borel theorem 31Ч32 35 130 164 Homeomorphism 144 158 Horizontal line test for uniform convergence 119Ч120 Image 62Ч63 Improper integrals 114 Increasing function 74 85 Increasing sequence 41 Induction 19 Inductive procedure 19 Infimum (inf) 38 Infinite discontinuity 71 Infinite sets 7Ч9 Infinitely often (i.o.) 49 Infs, properties of 39Ч40 integral see УRiemann Ч Stieltjes integralФ Integral test 115 Integration by parts 111Ч112 Interchange of operations 117Ч119 122Ч124 Interior of a set 145 Intermediate Value Theorem 75Ч76 Intermediate value theorem, for derivatives 87Ч88 Intersection 2 3 6 Invalid interchange of operations, examples of 117Ч119 Inverse image 59 Irrational numbers 147 Isolated point 21 Jump discontinuity 71 Jump function 102Ч103 l'Hospital's rule 81 88Ч90 Largest subsequential limit 46 Least upper bounds 38 Least upper bounds, and completeness 37Ч42 Left-continuous function 111 lim inf 46 lim sup 46 Limit concept, generalization of 45Ч48 Limit operations, and uniform convergence 122Ч125 Limit point 21 Limit, definition of 11 Limit, lower 46 Limit, upper 46 Line integrals, and Riemann Ч Stieltjes integral 104 Local concept of continuity 59 67 Local maximum 83 Local minimum 83 Logic 15Ч21 Logic, mathematical induction 18Ч19 Logic, negations 19Ч21 Logic, proof, types of 16Ч17 Logic, quantifiers 17Ч18 Logic, truth tables 15Ч16 Lower bound 38 Lower limit 46 Lower limit, properties of 49 Lower semicontinuous (LSC) function 152Ч158 Lower sum 94 Mapping 57 Mathematical induction 18Ч19 Maximum 65 83 Mean value theorem 81 83Ч85 Mean Value Theorem, applications of 86Ч91 Mean Value Theorem, for integrals 112Ч113 Mean value theorem, generalized 85Ч86 Metric 10 Metric space 10Ч13 Metric space, compactness criteria in 162Ч164 Minimum 65 83 Monotone function 74 Monotone sequence 41 124Ч125 Mutually exclusive sets 5 Negations 19Ч21 Neighborhood 155 Nested, Set Property 29 164Ч165 Nonsimple discontinuity 73 Nowhere dense sets 78 144Ч145 148 Open ball 11 Open sets 12 Open sets, continuity and 61Ч62 Open sets, relation between closed sets and 13Ч14 Open sets, unions and intersections of 25Ч28 Open subsets of R 42 Order of summation, reversal of 137Ч139 Partition 93 Partition, refinement of 95 Partition, size of 93 Path-connectedness 150Ч151 Perfect set 78 Piecewise continuous function 99 Point discontinuity 71 Pointwise bounded sequence of functions 132 Pointwise convergence 117Ч120 Pointwise convergence, vertical line test for 119Ч120 Power series, convergence of 52Ч55 Predicate 17Ч18 Preimage 59Ч61 Probability, and Riemann Ч Stieltjes integral 104 Proof: by cases 22 Proof: by contradiction 17 Proof: types of 17 Proof: via contrapositive 17 Proper subset 4 Proposition 15 Quantifiers 17Ч18 19 Radius of convergence 54 Ratio Test 53 Rational numbers 7 147 Real numbers 1 165 Real numbers, extended 35 Real numbers, upper/lower limits of sequences of 45Ч56 refinement 95 Relative topology 142 Removable discontinuity 71 Riemann integral 93ff Riemann Ч Stieltjes integral 93Ч116 Riemann Ч Stieltjes integral, change of variable formula 112 Riemann Ч Stieltjes integral, definitions 93Ч96 Riemann Ч Stieltjes integral, evaluation formula for 103 Riemann Ч Stieltjes integral, existence of 96 Riemann Ч Stieltjes integral, improper 114 Riemann Ч Stieltjes integral, integration by parts 111Ч112 Riemann Ч Stieltjes integral, line integrals and 104 Riemann Ч Stieltjes integral, Mean Value Theorem for 112Ч113 Riemann Ч Stieltjes integral, probability and 104 Riemann Ч Stieltjes integral, properties of 98Ч106 Riemann Ч Stieltjes integral, upper bounds on 113 Riemann Ч Stieltjes sum 94 Right-continuous function 110 Rolle's theorem 83Ч86 Root test 53Ч55 Semicontinuous functions 152Ч158 Separated sets 151 SEQUENCE 33Ч34 45Ч52 Sequence, and limit concept 45 Sequence, bounded 34 Sequence, Cauchy 24 40Ч41 124 164 Sequence, convergence of 10Ч15 Sequence, monotone 41 124Ч125 Sequence, unbounded 36 Sequences of real numbers, upper and lower limits of 45Ч56 Set-theoretic difference 6 Sets 1ff Sets, 148 Sets, 148 Sets, and category 2 145 Sets, bounded 29Ч35 161Ч162 Sets, Cantor 76Ч80 Sets, closed 12Ч14 25Ч28 Sets, closure of 21Ч22 Sets, co-finite 23 Sets, compact 30 Sets, complement of 2 3 6 Sets, connected 150Ч152 Sets, countable 7Ч10 Sets, dense 68 69 145Ч146 Sets, disjoint 5Ч6 151 Sets, distributive law for 2 Sets, empty 5
–еклама
 |
|
ќ проекте
|
|
ќ проекте



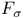 set
set  set
set