|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hanna J.R., Rowland J.H. Ч Fourier Series, Transforms, and Boundary Value Problems |
|
|
 |
| ѕредметный указатель |
Abbreviations, 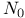 (set of natural numbers plus zero) 45 (set of natural numbers plus zero) 45
Abbreviations, AbelТs uniform convergence test 243
Abbreviations, AI (absolutely integrable) 107
Abbreviations, BVP* (boundary value problem) 1
Abbreviations, DFT* (discrete Fourier transform) 198
Abbreviations, FFT* (fast Fourier transform) 203
Abbreviations, IVP* (initial value problem) 2
Abbreviations, M (any set of n consecutive integers) 199
Abbreviations, N (set of natural numbers) 43
Abbreviations, ODE* (ordinary differential equation) 1
Abbreviations, PDE* (partial differential equation) 1
Abbreviations, PWC (piecewise continuous) 68
Abbreviations, PWS (piecewise smooth) 70
Abbreviations, SI (square integrable) 64
Abbreviations, SLDE* (Sturm Ч Liouville differential equation) 50
Abbreviations, SLP* (Sturm Ч Liouville problem) 50
Abbreviations, Z (set of all integers) 48
Absolutely integrable (AI) 107
Adjoint of operator 58
AiryТs equation 18
Approximation in mean 64 198Ч202
Arbitrary constants 1 6 11Ч12
Arbitrary functions 23 26 33
Associated Legendre differential equation 162
Associated Legendre functions 164
Associated Legendre polynomials 163
Auxiliary equation 5
Basic Fourier Series 72Ч74
bernoulli 68
Bessel equation 16 117
Bessel equation, modified type 121
Bessel equation, Sturm Ч Liouville type 134Ч135
Bessel functions 18 117 119
Bessel functions, boundedness of 132
Bessel functions, derivatives of 124Ч125
Bessel functions, first kind 18 119
Bessel functions, generating functions for 130
Bessel functions, graphs of 122
Bessel functions, integral form for 130Ч132
Bessel functions, integrals of 127Ч129
Bessel functions, modified 121
Bessel functions, norms 137
Bessel functions, orthogonal sets of 135 137
Bessel functions, second kind 121
Bessel functions, series of 137Ч139
Bessel functions, zeros of 134Ч137
Bessel transforms 210
BesselТs inequality 65
boundary conditions 2 24 219
Boundary conditions, Churchill type 248
Boundary conditions, Dirichlet type 247
Boundary conditions, linear homogeneous 219 222Ч225
Boundary conditions, Neumann type 248
Boundary conditions, nonhomogeneous 219 225
Boundary conditions, Robin type 248
Boundary value problems (BVPs) 1 24 219 270
Boundary value problems (BVPs), boundedness of solutions 36 222
Boundary value problems (BVPs), defined 24
Boundary value problems (BVPs), methods for solving 173 186 219 222Ч225 270Ч273 283Ч285 307-310
Boundary value problems (BVPs), solutions verified 225Ч228 242Ч245
Cauchy equation 7
Cauchy principal value 113Ч114
Cauchy Ч Kowalewsky theorem 25
Characteristic equations 5 8 27Ч31
Characteristic functions 50
Characteristic values 50
Classification, second order PDEs 23Ч24
Complete orthogonal sets 65Ч66
Complex conjugate 46Ч47 198
Complex-valued functions 46Ч47
Conduction of heat 236Ч238
Conductivity, thermal 236
Continuous functions 45 59
Continuous functions, piecewise (PWC) 68
Continuous functions, sectionally 68
Convergence in mean 64 66
Convergence of Fourier cosine series 78Ч79
Convergence of Fourier integrals 108
Convergence of Fourier series 75Ч76
Convergence of Fourier sine series 79
Convergence, point wise 66
Convergence, point wise, uniform, integrals 102Ч103
Convergence, point wise, uniform, series 58Ч59
Convolution 180Ч181
Convolution for Fourier exponential transforms 192Ч193
Convolution for Laplace transforms 180Ч181
Convolution for Mellin transforms 217
Cylindrical coordinates 140
Cylindrical coordinates, Laplacian in 141
Derivative, left hand 69
Derivative, right hand 69
Differential equations, Cauchy (Euler) 7
Differential equations, linear 2
Differential equations, linear homogeneous 2
Differential equations, nonhomogeneous 6
Differential equations, ODEs 1
Differential equations, PDEs 1
Differential equations, systems of 185
Differential operator 2
Differentiation of series 9 92Ч94
Diffusion, coefficient of 238
Diffusion, equation 238
Dirac delta function 177Ч179
Dirichlet problem 247Ч248
Discrete Fourier Transform 197Ч203
Discrete inner product 198
Discrete least squares approximation 198
Discrete norm 198
DТAlembert 68
dТAlembert solution of 28 34
dТAlembertТs solution 28 34
Eigenfunctions 50
Eigenfunctions, linear independence of 57
Eigenfunctions, series of 61 62
Eigenvalues 50
Elasticity, modulus 230
electrical circuits 271 273
Elliptic type, PDEs of 23Ч24
Error function 183 301Ч305
Euler 7 68
Euler, constant 120Ч121
Euler, differential equation 7
Euler, formulas 74
Euler, identity (relation) 32 112
Even function 76Ч77
Existence 2 25 169Ч170
Exponential, Fourier integrals 112Ч114
Exponential, Fourier series 80Ч82
Exponential, Fourier transforms 190 192
Exponential, function 5Ч6 30Ч31 46-48
Exponential, order 169
Exponential, solutions 5Ч6 30Ч31
Extension, nonperiodic 111
Extension, periodic 74 78
Fast Fourier Transform 203Ч205
Finite difference formulas 200
Finite difference method 241Ч242
Forward difference method 242
FOURIER 68
Fourier method of solution 222Ч225
Fourier method of solution, two dimensional 276Ч280
Fourier series 72Ч74
Fourier series in two variables 97Ч99
Fourier series, convergence 75Ч79
Fourier series, cosine 78
Fourier series, differentiation 92Ч94
Fourier series, exponential form 80Ч81
Fourier series, generalized 62
Fourier series, integration 94Ч96
Fourier series, sine 78Ч79
| Fourier series, uniform convergence of 89Ч92
Fourier sine integral formula 110
Fourier sine integral formula, theorem 75Ч76
Fourier sine integral formula, transforms of two variables 208Ч209
Fourier sine integral formula, transforms, cosine kernel 191
Fourier sine integral formula, transforms, exponential kernel 192
Fourier sine integral formula, transforms, sine kernel 191
Fourier Ч Bessel series 137Ч139
Fourier, constants (coefficients) 62Ч65 73Ч74 78Ч79 81
Fourier, cosine form 109Ч110
Fourier, cosine kernel for 189
Fourier, exponential form 112Ч113
Fourier, exponential kernel for 190
Fourier, finite transforms 189Ч190
Fourier, integral formula 107Ч108
Fourier, integral theorem 108 110Ч111
Fourier, method 219 270
Fourier, sine form 110
Fourier, sine kernel for 189
Functions, analytic 10 25
Functions, associated 164
Functions, Bessel 18 119Ч121
Functions, characteristic 50
Functions, complex-valued 46Ч47
Functions, continuous 45Ч46 59
Functions, error 183 301Ч305
Functions, even 76Ч77
Functions, exponential 5Ч6 30Ч31 46-48
Functions, gamma 117Ч119 170
Functions, generating for Bessel functions 130Ч132
Functions, generating for Legendre polynomials 149Ч151
Functions, harmonic 161 248
Functions, hyperbolic 47
Functions, inner product of 43 198
Functions, Legendre 144
Functions, normalized 43
Functions, norms of 43 198
Functions, odd 76Ч77
Functions, orthogonal 43
Functions, orthonormal 43
Functions, piecewise continuous 68Ч70
Functions, piecewise smooth 70
Fundamental interval 74
Fundamental set 4
Gamma function 117Ч119 170
Gauss Ч Seidel method 251Ч252
General solution 4 6 28Ч33
Generalized Fourier series 62
Generalized functions (or distributions) 179
Geometric series (progressions) 180 199
Gibbs phenomenon 86Ч88
Gram Ч Schmidt orthogonalization 44Ч45
Hadamard example 25Ч26
Hankel transforms 209Ч212
Harmonic analysis 82Ч84 198Ч202
Harmonic functions 161 248
Harmonic functions in cylindrical regions 260Ч263
Harmonic functions in half-plane 312
Harmonic functions in rectangular regions 248Ч251
Harmonic functions in spherical regions 267Ч268
Harmonic functions in strip 313Ч314
Heat conduction, equation 238
Heat conduction, experimental observations 236
Heat conduction, flow 236
Heat conduction, problem 236Ч238
Heat conduction, problem, solution 238Ч241
Heat conduction, problem, uniqueness 244Ч245
Heat conduction, problem, verification 242Ч244
Hermite polynomials 49
Hermitian orthogonality 47Ч49
Homogeneous equations 2 5Ч7 23
HookeТs law 270
Hyperbolic functions 47
Hyperbolic type, PDEs of 23Ч24
Improper integral, principal value of 113Ч114
Improper integral, uniform convergence of 102Ч103
Indicial equation 14
Indicial equation, roots of 14
Inequality, BesselТs 65
Inequality, Schwarz 46
Initial value problems (IVPs) 2Ч3 24
Inner product 40 43 198
inner product of functions 43
Inner product of vectors 40
Insulated surface 238 245 254 291
Integral equation 184
Integral form, BesselТs function 130Ч132
Integral theorem, Fourier 108
Integral transforms 168 189 191 208Ч210 214Ч215
Integral transforms, Fourier 191
Integral transforms, Fourier, cosine 191
Integral transforms, Fourier, exponential 192
Integral transforms, Fourier, finite 189Ч190
Integral transforms, Fourier, finite, cosine 189
Integral transforms, Fourier, finite, exponential 190
Integral transforms, Fourier, finite, sine 189
Integral transforms, Fourier, sine 191
Integral transforms, Fourier, two variables 208
Integral transforms, Hankel 209Ч210
Integral transforms, Hankel, finite 210
Integral transforms, kernels of 210
Integral transforms, Laplace 168
Integral transforms, Legendre 214
Integral transforms, Mellin 215
Integrating factor 50
Integration of series 94Ч96
Integro-differential equations 184
Interpolation 202
Inverse transforms 173 189Ч192 198 208Ч211 214 217
Jump discontinuity 69
Kernel 168
Kirchhoff s Law 271
LagrangeТs relation 58
Laguerre polynomials 49
Laplace transforms 168
LaplaceТs equation 247
Laplacian in cylindrical coordinates 141
Laplacian in rectangular coordinates 247
Laplacian in spherical coordinates 160Ч161 164
Least squares approximation 64Ч66
Left hand, derivative 69Ч70
Left hand, limit 68Ч69
Legendre, equation 12 142
Legendre, functions of second kind 164
Legendre, functions, associated 164
Legendre, polynomials 142 144
Legendre, polynomials, associated 162Ч163
Legendre, polynomials, derivatives of 148 151
Legendre, polynomials, generating functions 149
Legendre, polynomials, norms 153Ч154
Legendre, polynomials, orthogonal sets of 152Ч153
Legendre, polynomials, RodriguesТ formula 146Ч148
Legendre, polynomials, series of 154Ч155
Legendre, transforms 214Ч215
Liebmann method 251Ч252
Limits in the mean 64 66
Limits, one sided 68
Linear combinations 2 4
Linear combinations, extensions of, by integrals 111 297
Linear combinations, extensions of, by series 74 78 224Ч225 229 240 250
Linear dependence (independence) 3
Linear dependence (independence) of eigenfunctions 57
Linear dependence (independence) of functions 3
Linear differential equations 2 4Ч6 23
Linear operators 1Ч2
Linear operators, adjoint of 58
Linear operators, product of 2
Linear operators, self-adjoint 58
Linear operators, sum of 1
Liouville (Sturm Ч Liouville problem) 50
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



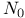 (set of natural numbers plus zero)
(set of natural numbers plus zero)