|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Asmar N.H. — Partial Differential Equations with fourier series and boundary value problems |
|
|
 |
| Предметный указатель |
Heat equation, solution with the Laplace transform 503
Heat equation, two dimensional 104 160
Heat equation, two dimensional with one radiating side 185
Heat equation, two dimensional, double Fourier series solution 161
Heat equation, two dimensional, nonhomogeneous 169
Heat equation, uniqueness of solution 189
Heat equation, varying the thermal diffusivity 124
Heat flux 143
Heat kernel 421
Heat problem in a bar insulated ends 146
Heat problem in a bar insulated lateral surface with non zero boundary conditions 140 142
Heat problem in a bar insulated lateral surface with zero boundary conditions 135
Heat problem in a bar with one radiating and one insulated end 152
Heat problem in a bar with one radiating end 147 450
Heat problem in a bar with two radiating ends 154
Heat problem in a thin circular ring 152
Heat problem with positive and negative separation constants 153
Heat source 143
Heat transfer constant 147 185 341 346
Heaviside unit step function 447 491
Heaviside unit step function, derivative of 448
Heaviside, Oliver 479
Heisenberg’s inequality 593
Heisenberg’s inequality for the Gaussian 595
Heisenberg’s uncertainty principle 573 574 590-592
Helmholtz equation 173 178 231
Helmholtz equation in a ball 291 293
Helmholtz equation in a disk 231 232
Helmholtz equation in rectangular coordinates 173
Helmholtz equation in spherical coordinates 291
Helmholtz equation, eigenvalues and eigenfunctions 293
Helmholtz equation, expansion in terms of the eigenfunctions of the 232 294
Helmholtz equation, three dimensional 178
Helmholtz equation, two dimensional 173
Hennite polynomial 332 597 606
Hennite polynomial, generating function for 608
Hennite polynomial, recurrence relation for 607
Hermite coefficient 599
Hermite function 410 580
Hermite series 581 599
Hermite’s differential equation 580 597
Hooke’s law 7
Hydrogen atom 573 582
Hydrogen atom and Schr dinger’s equation 582 dinger’s equation 582
Hydrogen atom and spherical harmonics 583
Hydrogen atom, bound state of the 585
Hydrogen atom, energy levels in the 585
Hydrogen atom, probability distribution lor the 586
Hydrogen atom, time-dependent wave function of the 586
Identity Principle A33
IDFT see "Inverse discrete Fourier transform"
Imaginary part 645
Impulse of a force 115
Incomplete gamma function 466 588 589
Indicial equation A54 238
Indicial root A54 238
Infinite square well 578
Initial condition A5 3 105;
Initial condition, radially symmetric 199
Initial point 612
Initial value problem A5
Initial value problem, existence and uniqueness of solutions of A6
inner product of functions 327
Inner product of vectors 326
Inner product with respect to a weight 330
Integral representation of Bessel functions 261 264
Integral representation of Legendre polynomials 307
Integral representation of modified Bessel functions 388
Inverse cotangent 653
Inverse discrete Fourier transform 561
Inverse Fourier cosine transform 35
Inverse Fourier sine transform 135
Inverse Fourier transform 398
Inverse Laplace transform 485
Inverse tangent 652
Isolated ,singularity 682
Isotherm 220 130 657 668
Iteration methods 541
Jacobi iteration 511 512
Jordan’s Theorem 612
Korteweg-de Vries equation 419
Lagnerre’s differential equation 584 600
Laguerre coefficient 601
Laguerre polynomial 332 584
Laplace transform 480
Laplace transform and ordinary differential equations 488 193
Laplace transform and rational functions 488
Laplace transform inverse of 185
Laplace transform involving unit step functions 492
Laplace transform of   , , 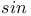  482 482
Laplace transform of 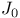 500 500
Laplace transform of  181 181
Laplace transform of convolutions 194
Laplace transform of derivatives 183
Laplace transform of functions of exponential order 180
Laplace transform of partial derivatives 502
Laplace transform of periodic functions 499
Laplace transform of the error function 501
Laplace transform of the Gaussian function 101
Laplace transform, delined 480
Laplace transform, derivatives of 183
Laplace transform, existence of 480
Laplace transform, linearity 182
Laplace transform, operational properties 182
Laplace transform, shifting on the 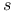 -axis 184 -axis 184
Laplace transform, shifting on the 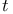 -axis 492 -axis 492
Laplace transform, table of A70
Laplace’s equation 541
Laplace’s equation in a disk 218
Laplace’s equation in a wedge 222
Laplace’s equation in cylindrical coordinates 228
Laplace’s equation in cylindrical coordinates, solution 228 229
Laplace’s equation in polar coordinates 216
Laplace’s equation in rectangular coordinates 163
Laplace’s equation in spherical coordinates 270 274 281
Laplace’s equation in spherical coordinates with symmetry 274
Laplace’s equation invariance by conformal mapping 664
Laplace’s equation, boundary condition 164 216
Laplace’s equation, discretization of 535
Laplace’s equation, iteration methods for 541
Laplace’s equation, maximum principle for 189
Laplace’s equation, product solutions in spherical coordinates 271 273
Laplace’s equation, radially symmetric 270
Laplace’s equation, separating variables in spherical coordinates 270
Laplace’s equation, three dimensional 469
Laplace’s equation, two dimensional 104 163
Laplace’s integral formula for Legendre polynomials 307
Laplacian 104
Laplacian in cylindrical coordinates 196
Laplacian in polar coordinates 194 196
Laplacian in spherical coordinates 196 497
Laplacian, Green’s formula for its integral 648
Law of conservation of heat energv 443
Lebesgue, Henri 389
Legendre coefficient 312
Legendre function 300 303
Legendre scries 270 312
Legendre series with decreasing coefficients 318
Legendre series, polynomial of polynomials 318
Legendre series, test for pointwise convergence 318
Legendre series, test for uniform convergence 318
Legendre, polynomial 273 275 301 308 328
Legendre, polynomial formula for the 303
Legendre, polynomial integral formula 315
Legendre, polynomial,  305 305
Legendre, polynomial,  304 309 304 309
Legendre, polynomial, Bonnet’s resurrence relation 309
Legendre, polynomial, generating function 307
Legendre, polynomial, Laplace’s integral formula for 307
Legendre, polynomial, leading coefficient of 302
| Legendre, polynomial, maxima and minima of 304
Legendre, polynomial, normalization of 302
Legendre, polynomial, orthogonality of 275 310
Legendre, polynomial, properties of 303 304
Legendre, polynomial, recurrence relation 309
Legendre, polynomial, recurrence relation for the coefficients 301
Legendre, polynomial, Rodrigues’ formula for 308
Legendre, polynomial, zeros of 304
Legendre’s differential equation A18 271 272 275 300 304
Legendre’s differential equation, solution by the method of power series 300
Legendre’s differential equation, used to compute areas 614
Leibniz rule 314
Liebmann’s iteration method 543
Line integral 643
Line of force 657
Line of heat flow 668
Linear correction term 82
Linear dependence for functions A7
Linear fractional transformation 675
Linear fractional transformation inverse of 676
Linear fractional transformation, composition of 676
Linear fractional transformation, determined bv three points 678
Linear fractional transformation, image of circle or a line by 678
Linear fractional transformation, is analvtic 675
Linear fractional transformation, is one to-one 676
Linear fractional transformation, mapping the disk to the upper half-plane 678
Linear fractional transformation, mapping the upper half-plane to the disk 678
Linear independence A7 326
Linear independence, Wronskian criterion for A7
Longitudinal vibrations of elastic bars 1 12
M bius transformation see "Linear fractional transformation" bius transformation see "Linear fractional transformation"
mass density 1 43
Maximum principle 169 187
Maximum principle for Laplace’s, equation 169 189
Maximum principle for the heat equation 188
Maximum principle, failure with internal source 492
Maximum principle, proof of the 190
Maximum-minimum principle 625
Mean square error 53
Mean square error in terms of an integral 53
Mean square error in terms of the Fourier coefficients 55
Mean value property of harmonic functions 623
Method of characteristic curves 5 108
Method of eigenfunction expansions 170 473 231
Method of Frobenius 51 2 37
Method of images 638
Method of power series 300
Method of separation of variables 13 115
Method of separation of variables and conformal mapping 669
Method of separation of variables in cylindrical coordinates 228
Method of separation of variables in polar coordinates 199 208
Method of separation of variables in quantum mechanics 573
Method of separation of variables in spherical coordinates 270
Method of separation of variables, applied to Schr dinger’s equation 575 dinger’s equation 575
Method of separation of variables, failure with nonhomogeneous problems 170
Method of separation of variables, gist of the 116
Method of successive overrelaxetion 543
Method of the Fourier transform 411- 413
Method of the Laplace transform 502
Method of undetermined coefficients A16
Method of undetermined coefficients, superposition rule for A17
Modified Bessel function 229
Modified Bessel function integral representation 388
Modified Bessel function, asymptotic formula 388
Modified Bessel’s equation 230 231 387
Moment of inertia 360 368
Moments of the Gaussian 596
Momentum of an electron 575 591
Momentum of an electron, as a Fourier transform 591
Multiply connected 613
Natural frequencv 72
Neumann condition 181 221
Neumann condition in a Poisson problem 688
Neumann condition in polar coordinates 221
Neumann condition on a rectangle 181
Neumann function 681
Neumann function and conformal mappings 687
Neumann function for regions depicted by figures 689
Neumann function for the first quadrant 688
Neumann function for the unit disk 690
Neumann function for the upper half-plane 686
Neumann function for unbounded regions 688
Neumann function, defined 681
Neumann function, normal derivative of 685
Neumann problem 441 442 618 619 684
Neumann problem in a rectangle 180
Neumann problem in the upper half-plane 645
Neumann problem on a disk 225
Neumann problem on simply connected region 684
Neumann problem, compatibility condition in 186 618
Neumann problem, solution by Neumann function 685
Neumann problem, solution in the upper half-plane 687 689
Neumann problem, solution on a disk 690
Neumann problem, uniqueness of solution 619
Newton’s law of gravitation 308
Newton’s second law of motion 7 574
Nodal line 160
Nonhomogencous heat equation on a half-line 470
Nonhomogencous wave equation, solved using Duhamel’s principle 174
Nonhomogeneous heat equation 463 165 169 473
Nonhomogeneous heat equation, solved using Duhamel’s principle 173
Norm of a function 327
Norm of a vector 326
Norm with respect to a weight 330
Normal dcrivative 617
Normal mode 10 70 118;
Normal mode for a rectangular membrane 157
Normal mode, amplitude of 73
Nyquist sampling rate 519
Open set 612
Operations on Fourier series 33
Ordinary differential equation A2
Ordinary differential equation in standard form A2
Ordinary differential equation with constant coefficients, general solution A15
Ordinary differential equation with constant coefficients, nth order A10
Ordinary differential equation, existence of fundamental sets of solutions A1
Ordinary differential equation, first order, linear A2
Ordinary differential equation, first order, linear, solution of A2
Ordinary differential equation, homogeneous A2
Ordinary differential equation, linear A2
Ordinary differential equation, nonhomogeneous A2
Ordinary differential equation, nonhomogeneous, general solution of A5
Ordinary differential equation, nonhomogeneous, particular solution of A5
Ordinary differential equation, order of A2
Ordinary differential equation, second order with constant coefficients A16
Ordinary differential equation, second order, general solution A16
Ordinary differential equation, solution of A2
Ordinary point A43 A51
Orthogonal functions 21 327
Orthogonal set of functions 327
Orthogonal trajectories 657
Orthogonal vectors 326
Orthogonality in Sturm - Liouville theory 336
Orthogonality of associated Legendre functions 322
Orthogonality of Bessel functions 250 252 338
Orthogonality of Chebyshev polynomials 315
Orthogonality of complex exponential system 65
Orthogonality of eigenfunctions in fourth order Sturm - Liouville problems 353
Orthogonality of eigenfunctions in Sturm - Liouville theory 336
Orthogonality of eigenfunctions of Helmholtz equation 232
Orthogonality of eigenfunctions of Helmholtz equation in a ball 293
Orthogonality of generalized Laguerre polynomials 603
Orthogonality of Hernite polynomials 598
Orthogonality of Laguerre polynomials 601
Orthogonality of Legendre polynomials 273 310 338
Orthogonality of spherical Bessel functions 261
Orthogonality of spherical harmonies 283
Orthogonality of trigonometric system 21
Orthogonality with respect to a weight 330 343
Orthonormal set of functions 327
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 dinger’s equation
dinger’s equation 
 ,
, 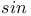
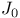

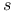 -axis
-axis 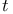 -axis
-axis 
