|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Adler S.L. Ч Quaternionic Quantum Mechanics and Quantum Fields |
|
|
 |
| ѕредметный указатель |
"Algebraic chromodynamics" 442n.20 473 479n.39
"Ghost" fermions 492n.48
"Mass gap" for constant quaternionic potential 126 527
"Quantization" of a classical theory 442n.20 533
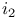 , real , real 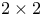 representation of i, adjoint introduced 346 representation of i, adjoint introduced 346
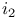 , real , real 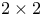 representation of i, defined 47 representation of i, defined 47
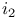 , real , real 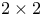 representation of i, transformation to bases which diagonalize 381 representation of i, transformation to bases which diagonalize 381
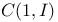 (complex subalgebra of left-acting algebra) 70 85 113 414 417 422Ч424 426Ч427 429 432 478 497 500 (complex subalgebra of left-acting algebra) 70 85 113 414 417 422Ч424 426Ч427 429 432 478 497 500
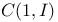 (complex subalgebra of left-acting algebra) and independent particle picture in Fock space 287 (complex subalgebra of left-acting algebra) and independent particle picture in Fock space 287
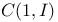 (complex subalgebra of left-acting algebra) and spin Hamiltonian 85Ч86 (complex subalgebra of left-acting algebra) and spin Hamiltonian 85Ч86
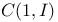 (complex subalgebra of left-acting algebra), asymptopia hypothesis 497Ч498 518Ч519 530 (complex subalgebra of left-acting algebra), asymptopia hypothesis 497Ч498 518Ч519 530
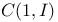 (complex subalgebra of left-acting algebra), conjugation 86 279 (complex subalgebra of left-acting algebra), conjugation 86 279
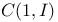 (complex subalgebra of left-acting algebra), spin matrices 84 (complex subalgebra of left-acting algebra), spin matrices 84
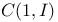 (complex subalgebra of left-acting algebra), unitary products of left algebra units in second quantization 278 (complex subalgebra of left-acting algebra), unitary products of left algebra units in second quantization 278
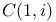 (complex subalgebra of quaternion) 34 59 61 63 66 70Ч72 75Ч76 78 80Ч81 115 117 119 122 132 141 148 152Ч156 159Ч160 166Ч167 171Ч174 196 207Ч209 230 233 242Ч243 245 247Ч248 251 253Ч260 262 270Ч272 278 287 289 291 296 314Ч315 329n.12 332 334 335n.14 340 340n.16 351 359Ч361 369 373Ч387 390Ч395 397Ч398 401 404Ч405 407 409Ч410 478 479n.39 527Ч530 (complex subalgebra of quaternion) 34 59 61 63 66 70Ч72 75Ч76 78 80Ч81 115 117 119 122 132 141 148 152Ч156 159Ч160 166Ч167 171Ч174 196 207Ч209 230 233 242Ч243 245 247Ч248 251 253Ч260 262 270Ч272 278 287 289 291 296 314Ч315 329n.12 332 334 335n.14 340 340n.16 351 359Ч361 369 373Ч387 390Ч395 397Ч398 401 404Ч405 407 409Ч410 478 479n.39 527Ч530
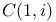 (complex subalgebra of quaternion) and matrix representations of symmetry generators 68 75Ч77 80Ч81 84 141n.6 238 (complex subalgebra of quaternion) and matrix representations of symmetry generators 68 75Ч77 80Ч81 84 141n.6 238
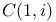 (complex subalgebra of quaternion) and nonrelativistic reduction of Klein Ч Gordon equation 321Ч322 (complex subalgebra of quaternion) and nonrelativistic reduction of Klein Ч Gordon equation 321Ч322
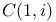 (complex subalgebra of quaternion) and zeroth-order basis rediagonalization in degenerate perturbation theory 142 (complex subalgebra of quaternion) and zeroth-order basis rediagonalization in degenerate perturbation theory 142
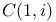 (complex subalgebra of quaternion) with i replaced by (complex subalgebra of quaternion) with i replaced by 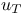 116 286 116 286
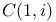 (complex subalgebra of quaternion) with i replaced by general unit quaternion 93 227 254 283 322 (complex subalgebra of quaternion) with i replaced by general unit quaternion 93 227 254 283 322
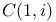 (complex subalgebra of quaternion), bases used to span quaternionic Fock space 271 (complex subalgebra of quaternion), bases used to span quaternionic Fock space 271
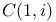 (complex subalgebra of quaternion), notation introduced 13 (complex subalgebra of quaternion), notation introduced 13
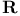 , reduction of wave packet operation 520 522Ч524 , reduction of wave packet operation 520 522Ч524
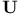 , unitary evolution operation 520 522Ч524 , unitary evolution operation 520 522Ч524
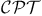 theorem 216 216n.13 531 theorem 216 216n.13 531
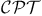 theorem, apparent violation for theorem, apparent violation for 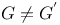 482n.42 531 482n.42 531
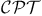 theorem, restrictions on theorem, restrictions on 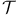 violation model 216 216n.12 violation model 216 216n.12
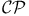 in time reversal violation model 216 in time reversal violation model 216
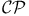 violation, phenomenological 215Ч217 508Ч509 531 violation, phenomenological 215Ч217 508Ч509 531
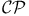 violation, phenomenological, Kobayashi Ч Maskawa form 216 518 violation, phenomenological, Kobayashi Ч Maskawa form 216 518
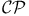 violation, phenomenological, magnitude of 215Ч217 violation, phenomenological, magnitude of 215Ч217
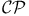 violation, phenomenological, milliweak 216 violation, phenomenological, milliweak 216
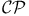 violation, phenomenological, superweak 216n.12 violation, phenomenological, superweak 216n.12
Abelian group 90Ч91 99Ч100
Abelian monopole 97n.8
Absolute value function see "Modulus function"
Absorption see "Scattering one-dimensional"
Action and Feynman path integral 110 353
Action as integral of Lagrangian density 375
Action, classical, not fundamental in quaternionic quantum mechanics 111Ч112
Action, invariance under 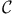 , ,  , , 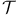 384Ч387 384Ч387
Action, principle for generalized dynamics 445Ч447
Action, real-valued, independent variations of 375
Adiabatic approximation 145Ч149 195n.2
Adiabatic approximation for zero energy state 148Ч149
Adiabatic approximation, effective expansion parameter for 147
Adiabatic switching 229
Adjoint defined for column vector 21Ч22
Adjoint defined for quaternion matrix 14
Adjoint of Grassmann quaternion 16
Adjoint of operator 22Ч23 51
Adjoint of product 15Ч16
Adjoint, relation between 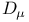 and and 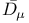 484 484
Adjoint, use of 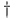 as notation for 14 236 323 330 as notation for 14 236 323 330
Albert's Theorem 7
Algebra of Dirac matrices and 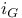 , , 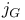 , , 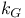 340 340n.16Ч17 340 340n.16Ч17
Algebra over reals 5Ч7
Algebra, "charge" for complex generator matrices 436
Algebra, "charge" for quaternionic generator matrices 434Ч437 452
Algebra, "color charge" 480 480n.40
Algebra, absolute valued 7
Algebra, angular momentum 65 85 90n.4 395
Algebra, angular momentum, one-dimensional representation of 396 434Ч435 515
Algebra, anticommutator, of Dirac matrices 330 335
Algebra, basis elements 6
Algebra, Clifford 10n.9 114n.16 514n.11
Algebra, Clifford, of (3, 1) signature and quaternions 512
Algebra, commutator, of Dirac matrices and 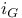 331 335 331 335
Algebra, complex 7
Algebra, complex, automorphism of 16n.16 30
Algebra, conformal, generators of 392
Algebra, conformal, nonzero energy quaternionic representations transformable to complex form 392
Algebra, division 8Ч9
Algebra, four-vector extension of quaternion 513 514n.11
Algebra, Grassmann 16
Algebra, Jordan 10Ч11
Algebra, Jordan, exceptional 11
Algebra, Jordan, infinite-dimensional 11
Algebra, Jordan, special 11
Algebra, left-acting 23Ч24 33 38Ч39 100n.10 see
Algebra, Lie, commutator 435Ч436
Algebra, Lie, generalized bracket 437 452
Algebra, multiquaternion 272n.1 479Ч480 511 530
Algebra, nonassociative 8 20 49Ч52 540
Algebra, noncommutative 7Ч8 11 20n.3 55 244 258
Algebra, octonion 7Ч8 11 49Ч52
Algebra, Poincare 361 388Ч398 429 489 530 see
Algebra, Poincare, nonzero energy quaternionic representations transformable to complex form 361Ч362 388Ч398 499 503 526 532
Algebra, Poincare, relation to locality 362 398
Algebra, quaternion 7 11Ч12 114
Algebra, quaternion, associativity of 12
Algebra, quaternion, automorphism of 16Ч17 30 515
Algebra, quaternion, complex 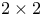 matrix representation 495 matrix representation 495
Algebra, quaternion, real matrix representations 10n.9
Algebra, right-acting 24Ч25 34 38Ч39 100n.10 275 399 480 512 530
Algebra, simple 11n.12
Algebra, SU(2) see "Angular momentum"
Algebra, supersymmetry 361
Analyticity properties 159 175
Analyticity properties of forward scattering amplitude 179Ч183 358 499 526
Analyticity properties of thermal Green's functions 291Ч293
Analyticity properties upper half plane, in decaying state theory 202Ч206
Angular momentum, algebra see "Algebra"
Angular momentum, analog of left- and right-ordered Fourier transform 84n.12
Angular momentum, anti-self-adjoint operator for 64Ч66 80 118Ч119
Angular momentum, anti-self-adjoint operator for, action in coordinate representation 64
Angular momentum, anti-self-adjoint operator for, action of time reversal on 118Ч119
Angular momentum, anti-self-adjoint operator for, commutation relations 65
Angular momentum, anti-self-adjoint operator for, eigenstates and spectrum of 65
Angular momentum, anti-self-adjoint operator for, eigenstates, ray convention for 65
Angular momentum, anti-self-adjoint operator for, rotation group constructed with 65
Angular momentum, anti-self-adjoint operator for, self-adjoint squared operator 65 80
Angular momentum, complex linear operators 66Ч68 351 408n.4 512
Angular momentum, complex linear operators, action of time reversal on 118Ч119
Angular momentum, ladder operators 66Ч68
Angular momentum, orbital 85 502n.6
Angular momentum, orbital, scalars with respect to 85
Angular momentum, orbital, vectors with respect to 85
Angular momentum, partial wave analysis 166 175
Angular momentum, representation 65Ч66
Angular momentum, representation, left-acting algebra I, J, K in 65Ч66
Angular momentum, representation, matrices 68
Angular momentum, representation, matrices, right action 68 80Ч81 503
Angular momentum, self-adjoint operator for 66Ч68 351 512
Angular momentum, self-adjoint operator for, action in 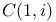 Hilbert subspace 66 166 Hilbert subspace 66 166
Angular momentum, self-adjoint operator for, commutation relations 66
Angular momentum, spin 84
Angular momentum, spin, algebra of 85
Angular momentum, spin, nonrotational invariance of J 85 130
Angular momentum, spin, operators 85 119
Angular momentum, spin, rotational invariance of 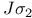 85 130 85 130
Angular momentum, total 85 90n.4
Angular momentum, total, action of time reversal on 119
Anomaly 387 387n.10 531
Anomaly, chiral 374 399 480 483 508
Anomaly, Witten 480
Anticommutation, assumption for symplectic components of fermions in charge conjugation analysis 384
Anticommutator in Foldy Ч Wouthuysen method 325
Anticommutator in Galilean analysis 93n.7 95
Anticommutator in uncertainty principle derivation 73
Anticommutator of 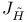 , , 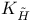 with with 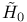 139 139
Anticommutator of annihilation and creation operators 273 417 503
Anticommutator of Dirac matrices 330
Anticommutator of quasiparticle operators 280 285Ч286
Anticommutator, canonical, in operator gauge invariant theory as constraint 463 512
Anticommutator, canonical, in operator gauge invariant theory biunitary transform covariant 529
Anticommutator, notation defined 16
Associator 539Ч540
Asymptotic completeness 265 265n.8 527
Asymptotic particle spectrum 388 391 397
| Asymptotic scattering states 4 66 128 188
Asymptotic scattering states in quantum chromodynamics 499n.3
Asymptotic scattering states, complex for suitable ray choice 63Ч64 159 160 172n.5 181 198 213 512
Asymptotic scattering states, dynamics of 113 497Ч499
Asymptotic scattering states, momentum operator definitions agree on 63Ч64
Asymptotic scattering states, structure, in multiparticle, multichannel scattering 254Ч262 see classification
Asymptotically 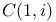 497Ч498 500 530 497Ч498 500 530
Asymptotically 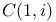 , analogy with asymptotically flat 64n.5 , analogy with asymptotically flat 64n.5
Automorphism of number field, defined 29n.7
Axial-vector current 374 531
Baker Ч Campbell Ч Hausdorff formula 90n.4 102 105 110Ч111 111n.14 245 393n.14
Bargmann potentials 526
Bell inequalities 524n.19
Berry's phase see "Phase geometric"
Bessel function of imaginary argument 137 137n.3 249n.4 311
Bessel function, spherical 167
big bang 532Ч533
Binding energies in atoms and nuclei 208
Birkhoff Ч von Neumann axioms 10Ч11
Bogoliubov transformation 533
Born approximation 174Ч175
Boson 238
Bound states 159Ч183 356
Bound states and potential component 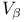 179n.7 526 179n.7 526
Bound states and scattering theory 225Ч227 225n.1
Bound states, disappearance from spectrum 163Ч164
Bound states, energy shift 177
Bound states, stabilized by rest mass 164Ч165 171 177Ч179 208 258
Bound-state-associated scattering resonances (resolvent singularities) 127 159 163Ч164 175Ч179 183 356
Bracket, classical Poisson 528 536 539
Bracket, generalized or generalized Poisson 398Ч399 447Ч448 528 see "Operator-valued "Total
Bracket, generalized or generalized Poisson of general trace functional with total trace Hamiltonian 447
Bracket, generalized or generalized Poisson of two conserved functionals is conserved 448
Bracket, generalized or generalized Poisson, algebra of total trace generators under 437 452
Bracket, generalized or generalized Poisson, antisymmetric in arguments 447
Bracket, generalized or generalized Poisson, Jacobi identity for 447Ч448
Bracket, generalized or generalized Poisson, Jacobi identity invalid in octonionic Hilbert space 539Ч540
Bracket, generalized or generalized Poisson, Jacobi identity proved 535Ч540
Bracket, generalized or generalized Poisson, Leibnitz product rule for 448
BRST transformation 529 529n.25
c-number 33 33n.9 374 384 384n.7 399 442 475 481Ч482 532 536
Causality 182 499 see Kramers
Center of mass, coordinate defined 81 238 255Ч256
Center of mass, N-pair model 245Ч246
Center of mass, separation of motion 81 233
Center of mass, separation of motion, complex cluster 255Ч256 261
Center of mass, separation of motion, quaternionic cluster 256 261
Center of mass, separation of motion, three-body 240Ч242
Center of mass, separation of motion, two-body 239Ч240
Chaos 524n.19 526n.23
Charge conjugation invariance 381Ч382 384Ч385 482Ч483
Charge conjugation invariance, 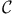 defined as behavior under sign reversal of imaginary terms in symplectic components 384Ч385 defined as behavior under sign reversal of imaginary terms in symplectic components 384Ч385
Charge conjugation invariance, analysis assumes symplectic components of fermions anticommute 384
Charge conjugation invariance, notation C in quaternionic quantum mechanics, and C in complex quantum mechanics and phenomenology 217n.14
Charge conjugation invariance, real phase factors in 385 482Ч483
Charge conjugation invariance, relationship between complex and quaternionic definitions 482n.42 529
Charge conjugation invariance, second, quaternionic definition for G = G' 385
Charge conjugation operation, used to relate antiparticle to particle states 502
Chiral components of fermion 387
Chiral components of fermion, coupled by quaternionic gauge interactions 388 508
Chiral projections in Majorana representation, do not commute with covariant derivative 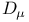 387Ч388 387Ч388
Classical state 4Ч5
Classical system 4Ч5 519n.14 520
Classical system, Feynman formulation (versus quantum) 4Ч5
Classical system, Markov property of 5n.3
Cluster decomposition property 233 240 245Ч254 293Ч299 518Ч519 527 see
Cocycle (2-cocycle) 100 100n.9 see projective
Coherent state 5 111n.14 528
Color degree of freedom 503 532
Commutativity of complex phase shifts 516Ч517 517n.12
Commutator in Foldy Ч Wouthuysen method 325
Commutator in Galilean invariance analysis 90n.4
Commutator in Schur's Lemma derivation 103
Commutator in uncertainty principle derivation 73
Commutator in virial theorem derivation 108
Commutator of annihilation and creation operators 273
Commutator of annihilation and creation operators in Heisenberg picture 211Ч212
Commutator of annihilation and creation operators in interaction picture 211
Commutator of annihilation and creation operators in Schroedinger picture 210 411Ч412 416 422
Commutator of conformal boost and dilatation with energy 392
Commutator of conserved observables with Hamiltonian 269n.11
Commutator of covariant derivatives 364Ч365
Commutator of covariant derivatives with chiral projectors 388 531
Commutator of fermionic supersymmetry generators with energy 392
Commutator of permutation operator with identical particle Hamiltonian 238
Commutator of quasiparticle operators 280 286 424
Commutator of S-matrix with free particle Hamiltonian 228
Commutator of S-matrix with translation generator 267
Commutator of symmetry generators with Hamiltonian 74 238
Commutator, algebra of group generators 434Ч436
Commutator, algebra of Poincare generators 389Ч390 398
Commutator, canonical, in operator gauge invariant theory, as constraint 459 512
Commutator, canonical, in operator gauge invariant theory, biunitary transform covariant 529
Commutator, canonical, in operator gauge invariant theory, nonlocal form and Bell inequalities 524n.19
Commutator, conditions for independent particle behavior 243Ч245
Commutator, conditions for reduction of Hamiltonian modulus to complex self-adjoint form 125
Commutator, corrections to quaternionic path integral 110Ч111
Commutator, notation defined 13
Commutator, parafermion-like, of quasiparticles 504
Complete orthonormal set in complex inner product 43Ч45 272n.1 409Ч410
Complete orthonormal set in quaternionic inner product 42Ч43 409Ч410
Complete orthonormal set in real inner product 45
Complete orthonormal set, relationship of complex to quaternionic 40Ч44 111n.14 230 212n.1 407Ч410 439Ч440
Completeness relation 26 28 180 248 538
Completeness relation and unitarity deficiency 226Ч227 265
Completeness relation for energy eigenstates, applied to optical potential 128Ч129
Completeness relation for full scattering states and bound states 226 265
Completeness relation for in and out scattering states 223Ч224
Completeness relation for Klein Ч Gordon equation 309Ч310
Completeness relation, fails in octonionic Hilbert space 49Ч50 51n.20
Complex analyticity 18 179Ч183
Complex cluster 255 287 532Ч533
Complex conjugate or conjugation 7 13 16n.16 43 47n.19
Complex conjugate or conjugation and Frobenius Ч Schur classification 437
Complex conjugate or conjugation as time reversal operator 47n.19 49 112 174
Complex conjugate or conjugation, notation * used for 13 43
Complex form, transformation of quaternionic matrices to 360Ч361 396
Complex free particle wave equations 397
Complex function theory 526
Complex Hilbert space see "Hilbert space i)$"/>
Complex number 3n.1 289n.8 see
Complex quantum field theory see "Quantum field theory"
Complex quantum mechanics 3 19 20n.3 24 26Ч27 29Ч30 33Ч34 37 46Ч49 53 58 69 75Ч77 89 98 100n.9 107Ч108 110Ч111 111n.14 161 163Ч165 167 173 179 183 197 217n.14 233 238 255n.6 358 405
Complex quantum mechanics and indefinite inner product for Klein Ч Gordon equation 306
Complex quantum mechanics as effective dynamics for observed physics 498Ч499
Complex quantum mechanics of one degree of freedom 442n.21
Complex quantum mechanics, bound states in 168
Complex quantum mechanics, canonical commutators in, are constraints in generalized quantum dynamics 399 455Ч475 512
Complex quantum mechanics, classical limit of 528
Complex quantum mechanics, cluster decomposition property in 250 296 298
Complex quantum mechanics, conserved observables in 269n.11
Complex quantum mechanics, conversion of anti-self-adjoint to self-adjoint operators in 76
Complex quantum mechanics, decaying state problem in 203
Complex quantum mechanics, Ehrenfest and virial theorems 352Ч353
Complex quantum mechanics, embedding of real quantum mechanics in 47Ч49
Complex quantum mechanics, existence of multilinear tensor product and reduction to independent one-body problems 242Ч243 271 523
Complex quantum mechanics, existence of multilinear tensor product and reduction to independent one-body problems, second quantized treatment 283Ч284 286Ч287
Complex quantum mechanics, external potential problem obtained from multiparticle 233
Complex quantum mechanics, Feynman path integral in 110 353Ч354 489 531
Complex quantum mechanics, Foldy Ч Wouthuysen reduction of relativistic equation yields 303 322 342
Complex quantum mechanics, Galilean invariance in 89 94
Complex quantum mechanics, generalized quantum dynamics with total trace Lagrangian applied to 442 455Ч475
Complex quantum mechanics, harmonic oscillator in 123
Complex quantum mechanics, identical particles in 238 270Ч271
Complex quantum mechanics, left-acting operator I commutes with all operators in 34 456 456n.27
Complex quantum mechanics, multilinear tensor product for 243Ч244
Complex quantum mechanics, nonlinear corrections to 442n.21 524Ч525 530
Complex quantum mechanics, nonlinear corrections to, parameterization of 525 525n.20
Complex quantum mechanics, nonlinear corrections to, possible link to hierarchy problem 525
Complex quantum mechanics, perturbation theory for 131
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



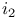 , real
, real 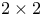 representation of i, adjoint introduced
representation of i, adjoint introduced 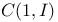 (complex subalgebra of left-acting algebra)
(complex subalgebra of left-acting algebra) 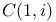 (complex subalgebra of quaternion)
(complex subalgebra of quaternion) 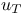
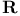 , reduction of wave packet operation
, reduction of wave packet operation 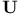 , unitary evolution operation
, unitary evolution operation 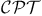 theorem
theorem 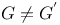
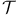 violation model
violation model 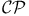 in time reversal violation model
in time reversal violation model 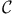 ,
,  ,
, 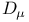 and
and 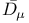
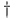 as notation for
as notation for 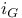 ,
, 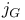 ,
, 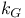
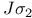
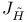 ,
, 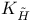 with
with