|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Adler S.L. Ч Quaternionic Quantum Mechanics and Quantum Fields |
|
|
 |
| ѕредметный указатель |
Multiparticle systems, center of mass separation, quaternionic cluster 256 261
Multiparticle systems, center of mass separation, three-body 241Ч242
Multiparticle systems, center of mass separation, two-body 239Ч240
Multiparticle systems, classification of asymptotic states 233 254Ч262 532Ч533
Multiparticle systems, classification of asymptotic states, assumptions made 254
Multiparticle systems, classification of asymptotic states, asymptotic Schroedinger equation 254Ч258
Multiparticle systems, classification of asymptotic states, complex cluster 255Ч256 287 518Ч519 532Ч533
Multiparticle systems, classification of asymptotic states, extension to positive cluster energies 260 287
Multiparticle systems, classification of asymptotic states, notation for partitioning in clusters 254
Multiparticle systems, classification of asymptotic states, null cluster 260
Multiparticle systems, classification of asymptotic states, quaternionic cluster 256 258 261 532Ч533
Multiparticle systems, classification of asymptotic states, wave function structure 256Ч262
Multiparticle systems, cluster decomposition property 233 240 245Ч254 293Ч299
Multiparticle systems, cluster decomposition property in finite subsystem of infinite system 253Ч254 293Ч299
Multiparticle systems, cluster decomposition property, breakdown 250 270 299 518Ч519 527
Multiparticle systems, cluster decomposition property, mean field approximation used to study 270 296Ч299
Multiparticle systems, cluster decomposition property, optical potential used to study 270 293Ч299
Multiparticle systems, energy, additive conservation law for 233 268Ч269 287
Multiparticle systems, energy, additive conservation law for, cluster energy conditions for 268 268n.10 287
Multiparticle systems, evolution operator factorization, complex case 244
Multiparticle systems, evolution operator factorization, failure in quaternionic case 245
Multiparticle systems, external potential problem obtained from 233
Multiparticle systems, Fock space 270Ч274 277 see second
Multiparticle systems, Fock space, class 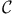 of complex bases 270Ч272 528 of complex bases 270Ч272 528
Multiparticle systems, Fock space, class 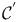 283 528 283 528
Multiparticle systems, Fock space, class 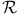 of real bases 275n.4 of real bases 275n.4
Multiparticle systems, Fock space, defined 273
Multiparticle systems, Fock space, dynamics 281Ч282
Multiparticle systems, Fock space, identity operator 274 277
Multiparticle systems, Fock space, inner product 271Ч272 281
Multiparticle systems, Fock space, N-particle Hilbert space component 273
Multiparticle systems, Fock space, vacuum state 273
Multiparticle systems, Galilean analysis 234Ч237
Multiparticle systems, Galilean analysis, assumptions 234Ч235 527
Multiparticle systems, Galilean analysis, summary 236
Multiparticle systems, general reduction for 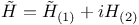 239Ч240 239Ч240
Multiparticle systems, Hamiltonian for 59Ч61 80Ч81 83 262
Multiparticle systems, Hamiltonian for, modeled as sum of one-body terms 242Ч243 270 283 509
Multiparticle systems, Hamiltonian for, noncommutativity and 244 283Ч285
Multiparticle systems, Hamiltonian for, quasiparticle transformation for 270 283Ч287
Multiparticle systems, Hamiltonian for, second quantized 270
Multiparticle systems, identical particles in 237Ч238
Multiparticle systems, independent particle behavior in complex specialization 245
Multiparticle systems, methods for 233Ч269
Multiparticle systems, momentum, in additive conservation law 233 267Ч268
Multiparticle systems, momentum, in anti-self-adjoint operator 59Ч60 80 238
Multiparticle systems, momentum, in anti-self-adjoint operator, action on asymptotic scattering states 261
Multiparticle systems, momentum, in anti-self-adjoint operator, commutes with S-matrix 267
Multiparticle systems, momentum, in anti-self-adjoint operator, eigenstates 61 76 255Ч256
Multiparticle systems, momentum, in self-adjoint operator 59Ч61
Multiparticle systems, momentum, in self-adjoint operator for individual particle 61
Multiparticle systems, momentum, in self-adjoint operator, action on asymptotic scattering states 261Ч262
Multiparticle systems, momentum, in total, as sum of cluster momenta 261
Multiparticle systems, N-pair model 245Ч254
Multiparticle systems, N-pair model, simplification in large N limit 250Ч251
Multiparticle systems, permutation, boson and fermion representations 238 270Ч271
Multiparticle systems, permutation, operator for coordinates 237Ч238
Multiparticle systems, permutation, order of P 271
Multiparticle systems, permutation, symmetry representations complex 238
Multiparticle systems, perturbation around 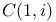 limit 245Ч254 limit 245Ч254
Multiparticle systems, perturbation around 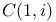 limit, zeroth-order approximation 247 limit, zeroth-order approximation 247
Multiparticle systems, quasiparticle operators 280 283Ч287 503Ч511 528
Multiparticle systems, quasiparticle operators, annihilate/create one-particle states 270 284 510
Multiparticle systems, quasiparticle operators, factor ordering in inversion formulas 284
Multiparticle systems, quasiparticle operators, noncanonical commutator/anticommutator 280 431 504 510
Multiparticle systems, quasiparticle operators, obey nonstandard exclusion principle 270 285
Multiparticle systems, quasiparticle operators, properties of 504Ч505 510
Multiparticle systems, quasiparticle operators, restrictions from time reversal 285Ч286
Multiparticle systems, scattering 61n.4 64 see multichannel
Multiparticle systems, Schroedinger equation for relative coordinate wave function 239 245Ч246
Multiparticle systems, Schroedinger equation for three-body problem 240Ч242
Multiparticle systems, Schroedinger equation, x-rep. projected from Fock space 282
Multiparticle systems, second quantization in  -representation 270Ч287 519 see "Fock "Quasiparticle -representation 270Ч287 519 see "Fock "Quasiparticle
Multiparticle systems, second quantization in  -representation, annihilation/creation operators 273 278Ч279 503 -representation, annihilation/creation operators 273 278Ч279 503
Multiparticle systems, second quantization in  -representation, annihilation/creation operators, commutator/anticommutator notation 273 -representation, annihilation/creation operators, commutator/anticommutator notation 273
Multiparticle systems, second quantization in  -representation, complete basis for Fock space 273Ч274 282n.6 -representation, complete basis for Fock space 273Ч274 282n.6
Multiparticle systems, second quantization in  -representation, Hamiltonian for 281Ч282 -representation, Hamiltonian for 281Ч282
Multiparticle systems, second quantization in  -representation, Hamiltonian for, n-body operator terms 282 -representation, Hamiltonian for, n-body operator terms 282
Multiparticle systems, second quantization in  -representation, Hamiltonian for, number conserving and nonconserving 281Ч282 528 -representation, Hamiltonian for, number conserving and nonconserving 281Ч282 528
Multiparticle systems, second quantization in  -representation, left-acting algebra 270 272n.1 274Ч278 503 -representation, left-acting algebra 270 272n.1 274Ч278 503
Multiparticle systems, second quantization in  -representation, left-acting algebra and change of representation 279 -representation, left-acting algebra and change of representation 279
Multiparticle systems, second quantization in  -representation, left-acting algebra and Hamiltonian structure 282 -representation, left-acting algebra and Hamiltonian structure 282
Multiparticle systems, second quantization in  -representation, left-acting algebra, complex conjugation * 279 419 430 -representation, left-acting algebra, complex conjugation * 279 419 430
Multiparticle systems, second quantization in  -representation, left-acting algebra, properties derived 275Ч278 -representation, left-acting algebra, properties derived 275Ч278
Multiparticle systems, second quantization in  -representation, left-acting algebra, properties stated 274Ч275 -representation, left-acting algebra, properties stated 274Ч275
Multiparticle systems, second quantization in  -representation, left-acting algebra, quaternion conjugation -representation, left-acting algebra, quaternion conjugation  282 282
Multiparticle systems, second quantization in  -representation, left-acting algebra, trace over defined 280 431 -representation, left-acting algebra, trace over defined 280 431
Multiparticle systems, second quantization in  -representation, notation used for operator and eigenvalue 275n.3 411n.6 -representation, notation used for operator and eigenvalue 275n.3 411n.6
Multiparticle systems, second quantization in  -representation, occupation number labels 274 -representation, occupation number labels 274
Multiparticle systems, second quantization in  -representation, particle number in cluster p of arrangement channel a 287 -representation, particle number in cluster p of arrangement channel a 287
Multiparticle systems, second quantization in  -representation, particle number, additive conservation law 287Ч288 -representation, particle number, additive conservation law 287Ч288
Multiparticle systems, second quantization in  -representation, particle number, operator 281 285 -representation, particle number, operator 281 285
Multiparticle systems, second quantization in  -representation, transformation to -representation, transformation to  -representation 277Ч279 277n.5 -representation 277Ч279 277n.5
Multiparticle systems, simplification by reraying 233 236Ч237
Multiparticle systems, statistical mechanics 287Ч293 527
Multiparticle systems, statistical mechanics, dilute regime 287
Multiparticle systems, statistical mechanics, equilibrium density matrix 288
Multiparticle systems, statistical mechanics, thermal averages 270
Multiparticle systems, statistical mechanics, thermal Green's functions 270 289Ч293
Multiparticle systems, symmetrization for identical particles 233 237Ч238 270
Multiparticle systems, tensor product 233 240Ч245
Multiparticle systems, tensor product, existence of complex multilinear 243Ч244
Multiparticle systems, tensor product, nonexistence of quaternion multilinear 233 244Ч245 250 258 280
Multiparticle systems, translation invariant 237Ч239 267
Multiparticle systems, translation invariant, three-body problem 240Ч242
Multiparticle systems, translation invariant, two-body problem 239Ч240
Multiparticle, multichannel scattering see also "Scattering" "S-matrix"
Multiparticle, multichannel scattering, S-matrix for 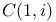 with standard ray choice 233 266Ч267 509 517 with standard ray choice 233 266Ч267 509 517
Multiparticle, multichannel scattering, S-matrix for definition and properties 266Ч267
Multiparticle, multichannel scattering, time-dependent formal theory of 233 262Ч269
Multiparticle, multichannel scattering, time-dependent formal theory of, a-state and integral equations 263Ч264
Multiparticle, multichannel scattering, time-dependent formal theory of, arrangement channel a defined 262
Multiparticle, multichannel scattering, time-dependent formal theory of, arrangement channel Green's functions 263
Multiparticle, multichannel scattering, time-dependent formal theory of, full Hamiltonian Green's functions 263
Multiparticle, multichannel scattering, time-dependent formal theory of, Hilbert spaces for 263
Multiparticle, multichannel scattering, time-dependent formal theory of, Moeller wave operators for channel a 264Ч267
Negative energy solutions, Dirac equation 333Ч334
Negative energy solutions, Klein Ч Gordon equation 314
Nernst theorem 46n.17
Neutron-optical experiments see "Experimental signatures for quaternionic quantum mechanics"
Noether theorem, total trace version 450Ч452
Noether theorem, total trace version, fermionic currents 484Ч486
Non-Abelian monopole 97n.8 528
Nonlinear modifications in quantum mechanics 524Ч525 see
Nonrelativistic kinematics 87 87n.1 89 164
Norm see "Quaternion" "Hilbert
Normalization for bound state 161 168
Normalization for Fourier expansion 307 411
Normalization, box 28
Number field, automorphism 29n.7 30
Number field, defined 9Ч10
Number field, generalized Wigner theorem for 29Ч31
Number field, rational 7n.6
Number field, rational, p-adic norm for 7n.6
Number field, topological characterization of 10n.9
Observables 27 35 58 108
Observables, conserved, conditions for 269n.11
Observables, identification in operator gauge invariant theories 452Ч453 453n.24 512 531
Octonion see "Algebra"
Octonionic quantum mechanics 9n.8 11 20 49Ч52 539Ч540
Octonionic quantum mechanics, attempted Schroedinger equation for 50Ч51
Octonionic quantum mechanics, failure of completeness in 49Ч50
Octonionic quantum mechanics, failure of cyclic trace property in 540
Octonionic quantum mechanics, failure of unitarity in 50Ч52
One quantum criterion 519 519n.14
Open questions 497
Open questions, involving quaternionic analogs of first quantized complex quantum mechanics topics 526Ч528
Open questions, involving quaternionic analogs of second quantization, relativistic quantum mechanics, and quantum field theory 528Ч533
Operator see also "Quaternion"
Operator, "time" 526n.22
| Operator, adjoint 22
Operator, annihilation for harmonic oscillator 209
Operator, annihilation, abstract 270
Operator, anti-Hermitian see "Quaternion anti-self-adjoint"
Operator, antiunitary 29Ч30 112 118Ч119 214
Operator, bosonic 289n.9 443
Operator, colinear and counitary 22 30
Operator, complex anti-self-adjoint, spectral theory 80
Operator, complex antilinear 43 see
Operator, complex linear 22 47n.19 49 53 61Ч63 66Ч68 118Ч119 351 408n.4
Operator, complex linear, defined in general case 61
Operator, complex self-adjoint, spectral theory 80 142 204
Operator, creation for harmonic oscillator 209
Operator, creation, abstract 270
Operator, dimension-6, and phenomenology of tests for quaternionic and nonlinear quantum mechanics 519Ч520 525
Operator, elliptic 127 172n.4
Operator, fermion grading 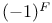 442Ч443 442n.20 443n.22 461 442Ч443 442n.20 443n.22 461
Operator, fermionic 289n.9 443
Operator, gauge transformation see "Operator-valued gauge transformation"
Operator, hermitian see "Quaternion self-adjoint"
Operator, left-acting algebra 23Ч24 33Ч34
Operator, left-acting algebra in angular momentum representation 65Ч66
Operator, left-acting algebra in coordinate representation 38
Operator, matrix elements, reality or complexity properties 34
Operator, mutually commuting set of self- and anti-self-adjoint, all Hermitian 77
Operator, mutually commuting set of self- and anti-self-adjoint, spectral theory of 53 76Ч83
Operator, noncompact 443n.22
Operator, nonlocal 83 127
Operator, normal 28n.6
Operator, product expansion 216
Operator, quaternion anti-self-adjoint 19 23 28n.6 31Ч36 53 76Ч83 103Ч104 118Ч119 448n.23
Operator, quaternion anti-self-adjoint, expectation value of 35
Operator, quaternion anti-self-adjoint, modulus (or magnitude) and phase of 33 35 77
Operator, quaternion anti-self-adjoint, not trivially made self-adjoint 77 448n.23 490Ч491
Operator, quaternion anti-self-adjoint, spectral theory of 29Ч36 76Ч83 91 98 124 134 136 494
Operator, quaternion anti-self-adjoint, spin 85
Operator, quaternion anti-self-adjoint, unitary inversion operator for 35 139 286
Operator, quaternion linear 22Ч23 27 61 66 408n.4
Operator, quaternion self-adjoint 19 23 27Ч29 62Ч63 69Ч71 76Ч83 103Ч104 108 397 448n.23
Operator, quaternion self-adjoint, expectation value of 28
Operator, quaternion self-adjoint, spectral theory of 27Ч29 76Ч83 103Ч104 494
Operator, quaternion self-adjoint, thermal expectation 288
Operator, quaternion unitary 30Ч31 36Ч37 41 54 65 68 70 74 90 99 101 103Ч105 109 113 208Ч209 228Ч232 432 440 523
Operator, quaternion unitary, spectral theory of 35Ч36 91
Operator, real anti-self-adjoint 47Ч48
Operator, real linear 48
Operator, real self-adjoint 47n.19 48
Operator, real skew-symmetric, canonical form for 47
Operator, unit see "Hilbert space unit
Operator, unitary 29Ч31 112
Operator-valued gauge transformation 399 442 442n.20Ч21 449Ч455 501 see generalized" "Generalized "Total
Operator-valued gauge transformation and complex quantum mechanics 455Ч475
Operator-valued gauge transformation, biunitary 431Ч432 449Ч450 483 529
Operator-valued gauge transformation, identification of invariant observables under 452Ч453 453n.24 512 531
Operator-valued gauge transformation, identification of invariant observables under, cotransforming states introduced 453
Operator-valued gauge transformation, summarized for quaternionic field models 475Ч478 483
Operator-valued gauge transformation, total trace Lagrangian invariant under 449Ч450 508
Operator-valued gauge transformation, unitary 431Ч432 449 529 see quaternion
Optical potential 114Ч115 127Ч128 177Ч179 183n.12 198n.4 218 499
Optical potential and cluster decomposition property 293Ч299
Optical potential and time reversal violation 114Ч115 129Ч130 174Ч175 215
Optical potential and time-dependent Schroedinger equation 128Ч130
Optical potential with spin 130Ч131
Optical potential, bound-state-associated resonances and singularities of 175Ч179
Optical potential, conjugate used in equation for 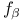 128 128
Optical potential, Galilean invariance 527
Optical potential, isolated singularity in 175
Optical potential, properties of 127Ч128
Optical potential, spin-0 obtained from spin-1/2 131
Optical potential, total 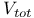 , applied 200Ч201 203Ч204 215Ч216 , applied 200Ч201 203Ч204 215Ч216
Optical potential, total 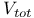 , defined 172 , defined 172
Optical theorem see "S-matrix unitarity
Parastatistics 238n.2 504Ч505 527
Parity, invariance 76 381Ч382 384 481Ч483
Parity, notation P in quaternionic quantum mechanics and  in complex quantum mechanics and phenomenology 217n.74 in complex quantum mechanics and phenomenology 217n.74
Parity, real phase factors in 384 481 483
Parity, relationship between complex and quaternionic definitions 482n.42
Path ordering operation 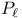 156 185 156 185
Pauli spin matrices 84 111n.14 184Ч185 322 330 479n.39
Pauli spin matrices, used to represent quaternions 495 527
Pauli spinors 401
Pauli spinors, origin of 515Ч516
Permutation operator 237Ч238
Permutation operator, square not assumed unity 238n.2
Perturbation theory, stationary state or time-independent 124 131Ч143 168Ч170
Perturbation theory, stationary state or time-independent for asymptotic bound on  138Ч139 138Ч139
Perturbation theory, stationary state or time-independent for multiparticle change from 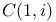 245Ч254 245Ч254
Perturbation theory, stationary state or time-independent for zero energy states 142Ч143
Perturbation theory, stationary state or time-independent, degenerate 140Ч143
Perturbation theory, stationary state or time-independent, dependence on origin of energy scale 134
Perturbation theory, stationary state or time-independent, first-order energy 133 177
Perturbation theory, stationary state or time-independent, first-order Hamiltonian modulus, phase 134Ч139
Perturbation theory, stationary state or time-independent, first-order left-acting algebra 134Ч139
Perturbation theory, stationary state or time-independent, first-order wave function 132Ч134
Perturbation theory, stationary state or time-independent, higher-order wave function 133Ч134 143
Perturbation theory, stationary state or time-independent, nondegenerate unperturbed energies 131Ч134 140
Perturbation theory, stationary state or time-independent, second-order energy and wave function 139Ч140
Perturbation theory, time-dependent 194Ч217
Perturbation theory, time-dependent in decaying state theory 201Ч208 213Ч217 499 526
Perturbation theory, time-dependent in decaying state theory, initial condition 201Ч202
Perturbation theory, time-dependent in decaying state theory, initial state 201
Perturbation theory, time-dependent in decaying state theory, mass and decay matrices 203Ч204
Perturbation theory, time-dependent in decaying state theory, upper half plane analyticity 202Ч206
Perturbation theory, time-dependent in decaying state theory, Weisskopf Ч Wigner approximation 202n.7 204Ч206
Perturbation theory, time-dependent in scattering theory 196Ч201
Perturbation theory, time-dependent in scattering theory, basic equation for 195 209
Perturbation theory, time-dependent in scattering theory, interaction picture 208Ч211
Perturbation theory, time-dependent in scattering theory, notation used for 194n.1
Perturbing Hamiltonian, compact notation for matrix elements 132 134 195
Phase of  -symplectic potential 114n.17 188 191 -symplectic potential 114n.17 188 191
Phase, approximation methods involving 145Ч158
Phase, dynamical (versus geometric) 148
Phase, geometric, adiabatic 145Ч149 527
Phase, geometric, analog in generalized dynamics 531
Phase, geometric, complex for nonzero energy 148
Phase, geometric, complex for nonzero energy, integral over closed orbit 148
Phase, geometric, complex for nonzero energy, reraying of 148
Phase, geometric, nonadiabatic 150Ч156
Phase, geometric, nonadiabatic and time-ordered integral properties 151Ч152
Phase, geometric, nonadiabatic, invariant angle associated with 152
Phase, geometric, nonadiabatic, quaternionic distinct from complex 153Ч156
Phase, geometric, nonadiabatic, quaternionic reraying of 152Ч156
Phase, geometric, nonadiabatic, Riccati equation and 153Ч155 527
Phase, geometric, nonadiabatic, trace of closed orbit integral 150Ч152
Phase, geometric, quaternionic for zero energy 149
Phase, geometric, quaternionic for zero energy, reraying of 149
Phase, geometric, quaternionic for zero energy, trace of closed orbit integral 149 152
Phase, role in generalized quantum dynamics 531
Phase, shift, in scattering 168 176
Phase, shift, in scattering, compound, and experimental tests 516Ч518
Planck scale (or mass) 497Ч498 500
Planck's constant 530 see
Potential see also "Hamiltonian" "Scalar "Scattering" "Schroedinger "Vector
Potential, anti-self-adjointness implies real part vanishes for single-component wave function 40 236
Potential, delta function 159
Potential, left-right symmetric in one-dimensional scattering 518
Potential, local 397Ч398
Potential, spherically symmetric 165Ч171 175Ч179
Potential, taken as a quaternionic constant 59n.3 113Ч114 123 125 137n.2
Potential, taken as a quaternionic constant, energy eigenstates for 125Ч126
Potential, time-independent and time reversal operator 112Ч119
Potential, translation invariance restrictions on 237
Pregeometry 511Ч512 511n.10 516 532
Preons 501Ч503 532 see
Preons, chiral symmetry and 508n.8
Preons, fundamental doublet assumed 502
Preons, fundamental doublet assumed, "rishons" or "quips" 502n.5
Prime as notation for x differentiation 184 358
Principal value P 56 127Ч128 177 203
Probability and Markovian property 5 5n.3
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



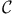 of complex bases
of complex bases 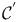
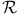 of real bases
of real bases 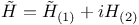
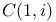 limit
limit  -representation
-representation 
 -representation
-representation 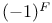
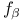
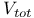 , applied
, applied  in complex quantum mechanics and phenomenology
in complex quantum mechanics and phenomenology 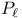

 -symplectic potential
-symplectic potential