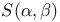|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Sheil-Small T. — Complex polynomials |
|
|
 |
| Предметный указатель |
Homology group of punctured plane 43
Homotopic 39
Homotopic curves 40
Homotopy classes 41
Homotopy group 42
Homotopy invariant 41
Hurwitz's theorem 65
Hyperbolic non-euclidean geometry 375
Ilieff — Sendov conjecture 206
Ilieff — Sendov conjecture, application of Grace's theorem 208—211
Ilieff — Sendov conjecture, case of real polynomial 216
Ilieff — Sendov conjecture, critical circle 225
Ilieff — Sendov conjecture, extremal distance 221
Ilieff — Sendov conjecture, extremal polynomial 223
Ilieff — Sendov conjecture, independent of particular zero 225
Ilieff — Sendov conjecture, nearest second zero 216
Ilieff — Sendov conjecture, proof for zeros on unit circle 207
Ilieff — Sendov conjecture, proof up to degree 5 211—212
Ilieff — Sendov conjecture, proof when zero at origin 216
Ilieff — Sendov conjecture, remaining zeros on unit circle 220
Ilieff — Sendov conjecture, upper bound on distance 215
Ilieff — Sendov problem see "Ilieff — Sendov conjecture"
Imaginary zeros 311—317
Implicit function theorem 63
Inequality for analytic polynomials 151—152
Inequality for harmonic polynomials 154
Inequality, implies surjectivity 101
Instantaneous double reversal 100—101
Integral mean theorem, zeros on unit circle 239
Integral representation of bounded convolution operator 168
Integral representation of Kaplan classes 293
Integral representation of non-vanishing polynomials 175
Interpretation of convolution conditions 270
Interspersed zeros and poles on unit circle 234
Interspersed zeros and poles, real rational functions 319
Interspersion lemma 232
Interspersion of zeros and local maxima 238
Interspersion theorem real meromorphic function 327
Interspersion theorem real rational functions 320
Interspersion theorem, unit circle 235
Inverse function 56
Inverse function inequality 356
Inverse function theorem 61
Inverse function, branch 58
Inverse function, continuation 57—58
Invertibility of harmonic multiplication operator 137
Inverting tract equation 18—19
Inverting transformation 18—19
Isolated zeros 8
Iterate 49
Jack, I.S. 266
Jacobian 61 124
Jacobian conjecture 81
Jacobian conjecture, algebraic resolution 124
Jacobian conjecture, condition in polar coordinates 88
Jacobian conjecture, degree of counter-examples 102—104
Jacobian conjecture, examples when true 87
Jacobian conjecture, proof for degree 2 85—86
Jacobian conjecture, proof under additional hypothesis 85
Jacobian conjecture, weak form 104—105
Jacobian determinant 61
Jacobian matrix 61
Jacobian operator, algebraic properties 91
Jacobian problem 89
Jacobian problem, geometric transformation 105
Jensen circle 304 305
Jordan curve 39
Jordan curve theorem 39
Jordan domain 39
Jordan polygon and dilatation criterion 404
Jordan polygon, mapping problem 402
Julia — Caratheodory lemma 330
Kaplan class 244 277 382 385
Kaplan class, coefficient bounds 294
Kaplan class, extreme points 293
Kaplan class, factorisation theorem 246
Kaplan class, integral representation 293
Kaplan class, K(1,1) 271
Kaplan class, linear functionals 293
Kaplan, W. 241
Keller Jacobian conjecture 87
Kernel 132
Knot 120
Krein — Milman theorem 287
Kristiansen, G.K. 240
Lagrange's interpolation formula 2
Laguerre — Polya class 347
Laurent expansion 126
Lax's theorem 153—154 186
Leading term 88
Length of curve 85
Level curve 66 306—307 350
Level curve of polynomials 351
Level curve, geometry 310
Level region 306 352
Level region and Smale's conjecture 364
Level region of rational function 353
Level region, convexity 360
Levin representation 332
Levin representation lemma 333
Lewandowski, Z. 242
Lewy's theorem 64
Limits of Suffridge's extremal polynomials 258
Linear form 181
Linear functional 131 177
Linear functional on Kaplan class 293
Linear functional on rational function 264—265
Linear operator 132
Linear operator lemma 272—273
Linear operator on polynomials 203
Linear operator on rational functions 264
Linear operator, Grace theorem 205
Linearly accessible domain 302
Liouville's theorem 26
Littlewood, J.E. 239
Lobachevsky 375
Local multiplicity 56
Local uniform convergence 128
Locally 1-1 24 82
Locally 1-1, function 56
Locally 1-1, harmonic functions 64
Locally 1-1, polynomial, topology 100
Locally bounded 128
Locating critical points 186
Location of zeros given critical points 201—202
Logarithm 28
Logarithmic derivative lemma 187
Logarithmic derivative, algebra 407
Logarithmic derivative, critical points 306
Logarithmic derivative, existence of non-real critical points 307
Logarithmic differentiation 23
Loop 28
Loop lemma 121
Lyzzaik, A. 392
Magnus theorem 109
Majorisation 171
Mapping problem for Jordan polygons 402
Marden, M. 206
Mason's theorem 370
Max-min inequalities 200—201
Maximum modulus 238
Maximum principle 57
Mean 145
Meromorphic function 27 45
Monodromy theorem 58
Multiple zeros 187
Multiplicity 22
Multiplicity of function at point 44
Multiplicity of harmonic function with polynomial co-analytic part 47
Multiplicity, analytic expression 24
| N-fold mapping and finite valence 390
N-fold mapping of circle 382—387
N-fold mapping, Fourier coefficients 391
n-valent 66
Nakai and Bab a theorem 111
NE convex 376
NE line 375
Nearest second zero 216
Negative type: strongly real rational function 321
Non-Euclidean line 375
Non-isolated zero 53
Non-real critical points of real rational function 323—324
Non-real zeros theorem 325
Non-separating lemma 119
Non-vanishing polynomials 173
Norm of operator 140
Norm of self-inversive polynomial 153
Normal family 128
Null homotopic 41
Number of isolated zeros of real analytic polynomial 8
Number of zeros 1
Number of zeros of real analytic polynomial 4
Open mapping 57
Order of critical point 353
Order of entire function 327
Order of meromorphic function 327
Orevkov, S.Yu. 118
Orientation 56
p-mean preserving operator 169
parabola 78
Parabolic region 78
Parametrisation 27
Parseval's formula 131
Partial fraction decomposition of rational function 355
Periodic 129
Pinchuk surface 100
Pinchuk's example 90—93
Pinchuk, S. 81 118
Plane topology 39
Poincare, H. 375
Poisson's formula 128
Polar coordinate 28
Polar coordinate form 82
Polar coordinate, Jacobian conjecture 88
Polar derivative 185
Pole 27 44
Polya and Schoenberg 161
Polya and Schoenberg's proof 161—165
Polya and Schoenberg's theorem 161
Polya — Schoenberg conjecture 260 275 276
Polya's theorem 347
Polynomial mean 145
Polynomial, constant on curve 84
Polynomial, non-vanishing 173
Polynomial, with all real zeros, Descartes' rule 318
Polynomial, with zeros on unit circle 231
Polynomially invertible 87 105
Popoviciu conjecture 407
Positive convolution operator 142
Positive harmonic function 142
Positive operator 138
Positive trigonometric polynomial 144—151
Positive trigonometric polynomial and convexity preserving operator 148
Positive trigonometric polynomial, representation 149
Positive trigonometric polynomial, representation theorem 150
Positive type, strongly real rational function 321
Positivity lemma 157
Prime degree 109—110
primitive 31
Problems 25—26 29 31 40 43 46—47 55—56 78—79 80 117 124 138 144 151—152 155—156 159—160 203 208 232 237—238 240 391—392
Projection onto plane 89
Projective plane 123
Properties of Sylvester resultant 12
Pseudo-surface 121 123
Pythagorean triples 372
Quadratic polynomials 373
Quadrilateral, harmonic mapping problem 405
Radical 23
Rado — Kneser — Choquet theorem 59 392
Ratio of linear functionals 180
Rational function in unit disc 193
Rational function with real critical points 325—326
Rational function, convolution containment theorem 265
Rational function, critical points 190
Rational function, distinct solutions 370
Rational function, Grace theorem 263
Rational function, linear functional theorem 264—265
Rational function, linear operator theorem 264
Rational function, proof of extended Grace theorem 269
Rational function, strongly real/interspersion theorem 320
Real analytic polynomial 4 27 81
Real analytic polynomial at infinity 13—19
Real critical point 325
Real polynomial 1 304
Real polynomial with imaginary zeros 311—317
Real polynomial, critical point 305
Real polynomial, Ilieff — Sendov conjecture 216
Real polynomial, representation as sum of polynomials with real zeros 322
Real rational function, critical point theorem 323—324
Real rational function, interspersed zeros and poles on real axis 319
Real rational function, representation in terms of strongly real rational functions 321
Real zeros, Descartes' rule 318
Rectilinear polygon 35
Relatively prime degrees 109—110
Removable singularity 44
Repeated asymptotic value curve 18
Repetition of asymptotic values 16
Repetition of reduction process 15
Repetition property 102 117
Repetition, third method 16—17
Representation for harmonic polynomial 3
Representation of complex polynomial 2 3
Representation of linear operator 132—133
Residue 43
Residue theorem 24 27
Resolving the singularity 13
Resultant 124
Resultant and Jacobian 124
Reverse inequalities 216
Reversed asymptotic value curve 18
Riemann mapping theorem 35 39
Riemann — Hurwitz formula 353
Robinson's conjectures 300—301
Robinson, S. 300 303
Rogosinski's coefficient theorem 170
Rogosinski's lemma 157
Rotation conjecture 392
Rouche's theorem 48
Rubinstein, Z. 207
Rule of signs, Descartes' 317
Ruscheweyh theorem for 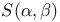 297 297
Ruscheweyh, St. 281
Schmeisser, G. 216
Schoenflies theorem 59
Schwarz function 168
Schwarz's lemma 60 234
Second derivative, non-real zeros 325
Second dual 172
Second zero 216
Self-intersections 123
Self-inversive polynomial 149 152 228
Self-inversive polynomial on unit circle 229
Self-inversive polynomial, norm theorem 153
Self-inversive polynomial, representation lemma 254
Self-inversive polynomial, zeros and critical points 230
Sendov, B. 206
Sense preserving 56 61
Sense reversing 56 61
Separated sets 30
Separation by a line 186
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте