|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ebbinghaus H.-D., Flum J. — Finite Model Theory |
|
|
 |
| Предметный указатель |
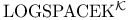 331 331
 246 246
 249 249
 39 39
![$EVEN[\tau]$](/math_tex/2510ee031669aa3c0fd774b52aa1483382.gif) 21 37 41 53 59 72 156 21 37 41 53 59 72 156
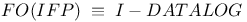 246 246
 155 155
![$FO[\tau]$](/math_tex/4aa3bc2a1b91dfb9f375ee432e17620d82.gif) 5 5
 219 219
 321 321
 72 72
 15 15
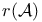 57 57
 50 50
![$[{\rm GFP}_{\overline{x},X}\;{\varphi}(\overline{x},X)]\overline{x}$](/math_tex/cc21ccf7ab475b78d8ca0bc6fafb28ff82.gif) 172 172
![$[{\rm IFP}_{\overline{x},X\varphi}]$](/math_tex/36df233b3911c6eb66d798b848aeb96182.gif) 169 169
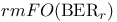 236 236
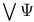 40 40
 7 7
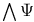 41 41
 179 179
 105 105
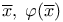 6 6
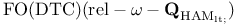 334 334
![$\rm FO(DTC)[rel-\omega-{\bf Q}_{{HAM}_{<}}]$](/math_tex/e1fea22d28f9d8d8c4a1f28e52a95b6282.gif) 328 328
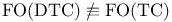 223 223
 273 273
 271 271
 270 270
 271 271
 269 269
 179 179
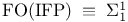 155 155
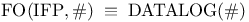 248 248
 210 210
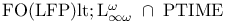 206 206
 244 244
 261 261
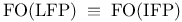 173 173
 203 204 203 204
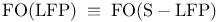 179 179
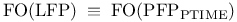 205 206 205 206
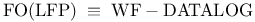 265 265
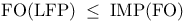 219 219
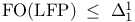 212 212
 249 249
 199 199
 224 224
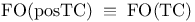 226 226
 243 243
 268 268
 268 268
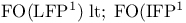 273 273
 268 268
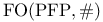 209 209
 209 209
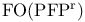 268 268
 205 205
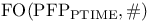 210 210
 221 221
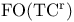 221 268 221 268
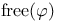 5 5
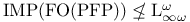 219 219
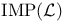 218 218
 14 14
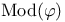 10 10
 15 15
 243 243
 211 211
 272 272
![$\rm Str[\tau]$](/math_tex/dcdb15d399f4196f637d5c59c93830b082.gif) 158 158
 332 334 332 334
 332 332
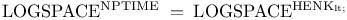 332 332
 334 334
 276 276
 38 38
 -structure 1 -structure 1
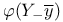 179 179
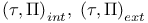 239 239
 242 242
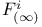 174 174
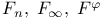 120 120
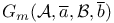 16 16
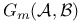 17 17
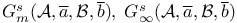 50 50
 50 50
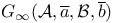 42 42
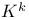 312 312
 64 64
 108 108
 71 71
 74 74
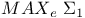 281 281
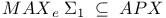 281 281
 334 334
 240 240
 309 309
![${Q}_{K}{{\overline{x}}_{1},...,{\overline{x}}_{s}}[{\psi}_{1}({\overline{x}}_{1}),...,{\psi}_{s}({\overline{x}}_{s})]$](/math_tex/1ac17fb486825224971fd9bbc8f3c33f82.gif) 308 308
 322 322
 1 1
 1 1
 125 133 125 133
 76 84 76 84
 45 73 45 73
 76 76
 78 78
 77 77
 77 77
 20 20
 52 52
 43 43
 208 208
 312 312
 179 179
 40 40
 8 8
 59 59
 7 7
 239 239
 105 105
 336 336
 54 54
![${\mathcal A}[\Pi],\;(\Pi,P)\overline{t}$](/math_tex/f92066f76343859cb8201788d674a70d82.gif) 240 240
![${\mathcal A}[\Sigma],\;(\Sigma,P)\overline{t}$](/math_tex/86b1ce38b40f228058d1f734a4cdda4e82.gif) 241 241
 3 3
 4 4
 9 9
![${\mathcal A}\models{\varphi}[{a}_{1},...,{a}_{n}],\;{\mathcal A}\models{\varphi}$](/math_tex/9a973327843399ffc091cc1014090b6782.gif) 6 6
 3 3
 4 4
 297 297
 48 48
 213 213
 42 42
 51 51
 38 38
 20 20
 43 43
 217 217
 14 14
 3 3
 24 24
 109 109
 331 331
 23 23
 309 309
![${\mathcal L}[{\bf Q}]$](/math_tex/ee6dded764a9239c91f2067a261f17e082.gif) 323 323
![${\mathcal L}[{\tau}]$](/math_tex/ddaa5126caa7364cc9d88224ee79dac582.gif) 122 122
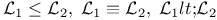 122 122
| ![${\mathcal L}{[\tau]}_{0},\;{\models}^{{\mathcal L},\tau}$](/math_tex/5501cdeb1caa4b685f1d2377c5b93fa882.gif) 289 289
 290 290
 296 296
![${\mathcal O}[{\sigma}]$](/math_tex/b287ec192019b198a38962d64a02897282.gif) 3 3
 4 4
 50 50
 6 6
 7 7
 38 38
 52 52
 60 60
 155 155
 242 242
 59 59
 59 59
 59 59
 243 243
 47 47
 40 40
 47 47
 314 314
 213 213
 38 38
 106 106
 7 7
![${\rm Str}[\tau]$](/math_tex/c78fb2a3cdb17aebab9c1c1f1ccef41c82.gif) 158 158
 229 229
 26 26
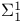 and NPTIME 139 150 151 157 and NPTIME 139 150 151 157
 86 86
 7 7
 1 1
 3 3
 156 156
 239 239
 6 6
 7 7
 10 10
 8 8
 18 18
 5 5
 322 322
 131 131
 107 107
 4 4
(M,f) 290
(M,O) 331
ACCEPT 126 132
Acceptable 126
Acceptor 162
Almost all 72
Alphabet 105
Antitone 167 172 192
Approximable 280
APX 281
Arity 1
Arity hierarchy 268 272 273
Arity, of a quantifier 309
ASSIGNMENT 6
ATC 261
Automaton 106
Automaton, deterministic 106
Automaton, nondeterministic 106
Axiomatizable, in  333 334 333 334
Axiomatizable, in  333 334 333 334
Axiomatizable, in  54 54
Axiomatizable, in  53 53
Axiomatizable, in  53 53
Axiomatizable, in  41 41
Axiomatizable, in a logic 124
Axiomatizable, in FO 14 20 150 252
Axiomatizable, in FO(M-LFP) 217
Axiomatizable, in SO 150
Back property 20
Back property, s- 51
Ball 26
Ball, r- 26
Base of an instruction 132
Basic term 248
Beth property 63
Beth's theorem 63
Blank letter 125 130
Body of a clause 239
Bounded 57 58
Bounded, fixed-point 204
Bounded, s- 57
Breadth, of a DATALOG program 242
Breadth, of an S-DATALOG program 242
Canonization,  294 294
Canonization,  on S 301 on S 301
Canonization, LOGSPACE- 294
Canonization, PSPACE- 294
Canonization, PTIME- 291—293
Capture 157
Capture, a complexity class 151 288
Capture, effectively strongly 290 295 325
Capture, effectively strongly on S 296
Capture, PTIME effectively strongly 290 292 294 300
Capture, PTIME effectively strongly on GRAPH 300
Capture, strongly 157 288
Cardinality 4
cell 125
Cell, virtual 125 130
Circuit, Hamiltonian 2 113 327
Class, bounded 57
Class, elementary 14
Class, elementary relative to 14
Class, finitely axiomatizable 14
Class, fixed-point bounded 204
Class, free parametric 80
Class, indiscernible 222
Class, nontrivial free parametric 80
Class, nontrivial parametric 77
Class, of finite structures 14
Class, of structures 10
Class, parametric 75
Class, s-bounded 57
Class, s-rigid 204
Clause 239
CLIQUE 2 113
Closed subset 222
Closed under isomorphisms 10
Closure, alternating transitive 261
Closure, deterministic transitive 123 220
Closure, plus 108
Closure, positive 108
Closure, transitive 123 220
Co-NPTIME 157
Colour type 61
Compactness Theorem 8
Compatible 76
Complement of a complexity class 155
Complete, NPTIME- with respect to FO(DTC) reductions 328
Complete, NPTIME- with respect to logspace reductions 327 328
Complete, strongly PTIME- with respect to FO-reductions 325
Complete, with respect to  -reductions 321 -reductions 321
Complete, with respect to 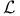 -reductions 324 -reductions 324
Completeness theorem 8
Complexity class, as a class of ordered structures 153
Complexity class, in complexity theory 153
Component, connected 2 30
Component, of a graph 2
Computable, PTIME- 204 291
Concatenation of languages 107
Configuration 128 134
Configuration, accepting 134
Configuration, oracle 331
Configuration, starting 136
Conn 2 23 122
Connected component 30
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



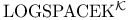



![$EVEN[\tau]$](/math_tex/2510ee031669aa3c0fd774b52aa1483382.gif)
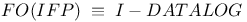

![$FO[\tau]$](/math_tex/4aa3bc2a1b91dfb9f375ee432e17620d82.gif)




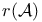

![$[{\rm GFP}_{\overline{x},X}\;{\varphi}(\overline{x},X)]\overline{x}$](/math_tex/cc21ccf7ab475b78d8ca0bc6fafb28ff82.gif)
![$[{\rm IFP}_{\overline{x},X\varphi}]$](/math_tex/36df233b3911c6eb66d798b848aeb96182.gif)
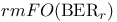
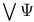

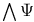


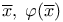
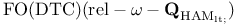
![$\rm FO(DTC)[rel-\omega-{\bf Q}_{{HAM}_{<}}]$](/math_tex/e1fea22d28f9d8d8c4a1f28e52a95b6282.gif)
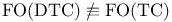






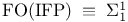
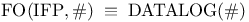

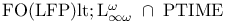


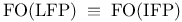

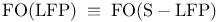
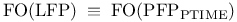
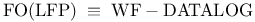
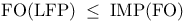
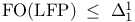



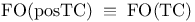



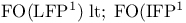

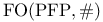

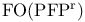

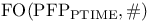

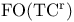
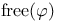
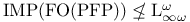
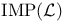

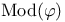




![$\rm Str[\tau]$](/math_tex/dcdb15d399f4196f637d5c59c93830b082.gif)


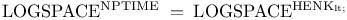



 -structure
-structure 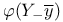
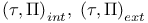

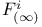
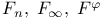
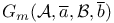
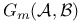
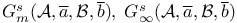

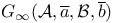
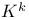




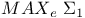
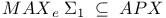



![${Q}_{K}{{\overline{x}}_{1},...,{\overline{x}}_{s}}[{\psi}_{1}({\overline{x}}_{1}),...,{\psi}_{s}({\overline{x}}_{s})]$](/math_tex/1ac17fb486825224971fd9bbc8f3c33f82.gif)
























![${\mathcal A}[\Pi],\;(\Pi,P)\overline{t}$](/math_tex/f92066f76343859cb8201788d674a70d82.gif)
![${\mathcal A}[\Sigma],\;(\Sigma,P)\overline{t}$](/math_tex/86b1ce38b40f228058d1f734a4cdda4e82.gif)



![${\mathcal A}\models{\varphi}[{a}_{1},...,{a}_{n}],\;{\mathcal A}\models{\varphi}$](/math_tex/9a973327843399ffc091cc1014090b6782.gif)


















![${\mathcal L}[{\bf Q}]$](/math_tex/ee6dded764a9239c91f2067a261f17e082.gif)
![${\mathcal L}[{\tau}]$](/math_tex/ddaa5126caa7364cc9d88224ee79dac582.gif)
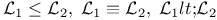
![${\mathcal L}{[\tau]}_{0},\;{\models}^{{\mathcal L},\tau}$](/math_tex/5501cdeb1caa4b685f1d2377c5b93fa882.gif)


![${\mathcal O}[{\sigma}]$](/math_tex/b287ec192019b198a38962d64a02897282.gif)





















![${\rm Str}[\tau]$](/math_tex/c78fb2a3cdb17aebab9c1c1f1ccef41c82.gif)


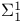 and NPTIME
and NPTIME 





















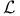 -reductions
-reductions