Авторизация
Поиск по указателям
Arratia R., Barbour A.D., Tavare S. — Logarithmic Combinatorial Structures: A Probabilistic Approach
Обсудите книгу на научном форуме Нашли опечатку?
Название: Logarithmic Combinatorial Structures: A Probabilistic ApproachАвторы: Arratia R., Barbour A.D., Tavare S.Аннотация: The elements of many classical combinatorial structures can be naturally decomposed into components. Permutations can be decomposed into cycles, polynomials over a finite field into irreducible factors, mappings into connected components. In all of these examples, and in many more, there are strong similarities between the numbers of components of different sizes that are found in the decompositions of "typical" elements of large size. For instance, the total number of components grows logarithmically with the size of the element, and the size of the largest component is an appreciable fraction of the whole.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2003Количество страниц: 363Добавлена в каталог: 18.11.2009Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
156 156 25 237 225 225 168 2 11 35 66 149 155 1 11 35 155 226 231 21 226 231 209 226 231 15 67 226 60 153 153 78 23 108 23 71 113 107 153 153 107 156 156 243 332 2 18 29 35 35 149 23 23 177 36 52 25 23 117 21 154 82 86 282 86 188 153 154 188 296 225 10 18 15 35 126 69 149 201 154 154 216 78 19 11 218 80 85 21 21 126 168 14 26 28 35 125 126 153 188 112 155 71 71 166 167 197 167 256 129 170 318 133 154 154 66 153 153 153 155 154 252 216 214 168 213 252 288 190 187 324 310 310 206 45 200 73 121 120 11 153 153 191 153 153 22 237 180 104 45 200 154 155 72 177 72 177 22 153 153 185 3 65 125 70 155 219 220 153 155 155 125 19 Additive functions 200—224 Additive semigroup, arithmetic 45 200—224 Additive semigroup, Erdos — Wintner theorem 203 Additive semigroup, Erdos — Wintner theorem, rate 209 Additive semigroup, Kubilius Main Theorem 214 Additive semigroup, Kubilius Main Theorem, functional 216 Additive semigroup, Kubilius Main Theorem, functional rate 217 Additive semigroup, regular variation, convergence 220 Additive semigroup, regular variation, functional rate 221 Additive semigroup, slow variation, convergence 214 Additive semigroup, slow variation, functional rate 217 Age-ordering 24 Aldous, D.J. 40 43 175 Approximation of 282 Approximation of 282 Approximation of 277—282 Approximation of 280 Approximation of 279 Approximation of 282—283 Approximation of 282 Approximation of 276 Approximation of 272 Approximation of 274 Approximation of 277 Approximation of 267—277 Approximation of 292 Approximation of 288—297 Approximation of 289 Approximation of 294 Approximation of 293 Approximation of 296 Approximation of 294 Approximation of 267 Approximation of 268 Approximation of 267—282 Approximation of 285—299 Approximation of 282—283 Approximation of 297—299 Approximation, Brownian 171—175 Approximation, Brownian, group order 199 Approximation, discrete 149 Approximation, global 71 97 Approximation, global, all components 168 Approximation, global, large components 167 Approximation, global, small components 165 Approximation, local 71 151 Approximation, local, large components 169 Approximation, local, small components 169 Approximation, normal 187 Approximation, normal, group order 199 Approximation, Poisson 186 191 328 Approximation, Poisson-Dirichlet 175—186 Approximation, total variation 226 Arratia, R. 3 7 16 22 23 26 29—31 43 46 47 100 103 104 115 123 125 141 143 166 167 170 171 173—175 187 189 191 199 202 Assemblies 45—46 48—49 54 59 60 70—73 133 139—140 Assemblies, logarithmic 51 70 Asymptotic independence 66 71 Bach, E. 7 31 Balakrishnan, N. 61 Barban, M.B. 29 Barbour, A.D. 7 16 17 20 21 23 26 43 67 100 123 125 166 167 170 173—175 186 187 189—191 199 202 225 309 Barouch, E. 79 Barton, D. 14 Bell numbers 37 Bell, J.P. 134 Bender, E.A. 134 Bergeron, F. 5 Bernoulli, random variables 19 55 58 145 156 186 236 Bernoulli, representation 19 20 101 Best, M.R. 25 Beta random variables 107 119 120 122 Beurling generalized primes 45 Beurling, A. 45 Billingsley, P. 7 28 30 31 Binomial random variables 51 Bollobas, B. 38 39 176 Bovey, J.D. 25 Brenti's representation 187 Brenti, F. 187 Brownian motion 20 216 Buchstab's function 22 87—89 Buchstab, A.A. 7 22 Cameron, P.J. 134 Car, M. 163 164 186 302 Card shuffling 44 Cayley, A. 41 Central limit theorem 103 Central limit theorem, functional 20 30 103 171—175 216 Central limit theorem, permutations 19 Central limit theorem, prime factorizations 30 Chen, L.H.Y. 73 225 Chistyakov, V.P. 4 Coagulation 63—64 Coloring 56—57 Completely additive 201 Component spectrum 1 35 Components, fixed number of 101 134 Components, functional limit theorem 216 Components, large 66 71—73 149—151 167 202 Components, largest 130 Components, number of 186—199 Components, small 66 71—73 96—100 151—152 165 202 Components, smallest 128 Conditioning Relation 2 15 26 32 34 48 69 77 97 111—113 125 149 155 Conditioning Relation, general statement 35 65 Conditions, G, A, D, B 156 Conditions, general 155—157 Conventions, general 155 Coupling 181—186 Coupling, Feller 100 181 Coupling, operational time 182 Coupling, Poisson process 181 182 Csoergo, M. 175 217 Daley, D.J. 121 David, F.N. 14 de Montmort, P.-R. 9 Decomposable 35 Delange, H. 29 DeLaurentis, J.M. 20 25 171 Derangement 13 Devroye, L. 61 Diaconis, P. 4 17 39 44 61 Diamond, H.G. 45 Dickman's function p 22 85 Dickman, K. 7 22 85 Dissected representation 153 155 163 167 Distance, bounded Wasserstein 174 187 209 226 231 Distance, Kolmogorov 226 231 Distance, total variation 15 67—70 226 Distance, Wasserstein 185 226 231 Distinct, component sizes 57 Distinct, parts of a multiset 57 Divisor function 158 Donnelly, P. 7 31 103 119 171 Dudley, R.M. 67 207 Elliott, P.D.T.A. 7 29 Engen, S. 107 119 Erdos — Turan theorem, functional rate 199 Erdos — Turan theorem, rate 199 Erdos — Wintner theorem 203 Erdos, P. 7 25 30 115 199 Ewens sampling formula 3 11 60—64 66 77—124 149 155 168 177 181 186 199 202 Ewens, W.J. 61 96 Exponential random variables 118 122 Factorial, falling 11 Factorial, moments 12 59 96 Factorial, rising 19 Feller coupling 16—18 100 181 Feller, W. 16 20 100 Fienberg, S.E. 61 Finite fields, random nonsingular matrices 44 Finite fields, random polynomials 43 Flajolet, P. 5 40 43 44 47 Foata, D. 5 46 Freedman, D. 4 Fristedt, B. 4 37 Functional central limit theorem 30 Functional central limit theorem, general 171—175 Functional central limit theorem, permutations 20 103 Functional central limit theorem, prime factorizations 30 G(n) 200 GEM, density 107 119 GEM, distribution 25 31 107 117—124 GEM, process 117—124 Generalized primes 45
Реклама
 |
|
О проекте
|
|
О проекте



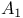
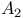
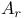
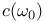
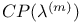
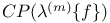
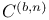
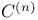
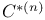
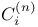
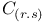
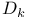
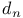
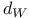
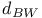
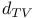
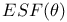
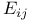
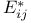
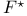
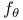
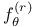
![$f_\theta^{[r]}$](/math_tex/89449f93fde45276e4bfc4264b4ef66a82.gif)
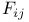
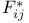
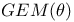
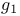

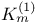
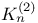
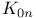
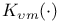
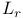
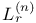
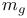
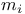
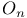
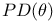
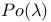
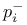
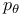
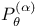
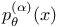
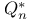
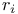
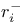
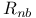
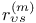
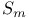
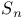
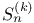
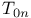
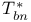
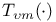
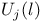
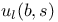
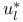
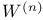
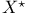
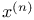
![$x^{[r]}$](/math_tex/2b89c79739d6eb05fda5f1740b25828f82.gif)
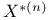
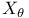
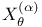
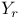
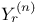
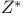
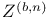
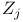
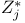
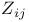
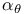
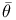
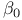
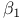
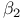
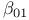
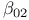
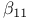
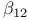

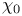
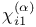
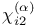

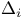
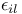
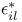
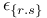
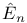
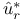
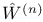
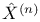
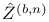
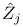
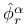
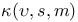
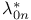
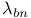
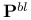
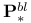
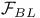
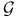
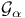
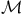
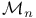
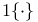
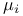
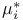
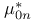
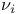
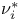
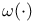
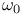
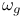
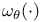
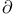
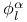
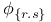
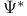
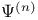
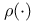
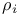
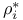
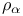

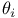
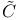
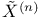
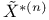
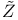
![$\tilde Z[a,b]$](/math_tex/09d0249de5769867567d2bc9b8971dcd82.gif)
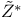
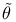
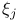
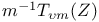 by
by 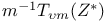 by
by 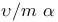
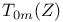 by
by 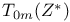 , Kolmogorov
, Kolmogorov 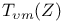 by
by 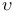
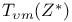 in distribution
in distribution 