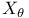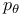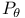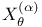Авторизация
Поиск по указателям
Arratia R., Barbour A.D., Tavare S. — Logarithmic Combinatorial Structures: A Probabilistic Approach
Обсудите книгу на научном форуме Нашли опечатку?
Название: Logarithmic Combinatorial Structures: A Probabilistic ApproachАвторы: Arratia R., Barbour A.D., Tavare S.Аннотация: The elements of many classical combinatorial structures can be naturally decomposed into components. Permutations can be decomposed into cycles, polynomials over a finite field into irreducible factors, mappings into connected components. In all of these examples, and in many more, there are strong similarities between the numbers of components of different sizes that are found in the decompositions of "typical" elements of large size. For instance, the total number of components grows logarithmically with the size of the element, and the size of the largest component is an appreciable fraction of the whole.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2003Количество страниц: 363Добавлена в каталог: 18.11.2009Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Generating function 19 Generator approach 226 Geometric random variables 28 GF(q) 43 Gnedin, A.V. 119 176 Goh, W.M.Y. 44 171 187 Golomb, S.W. 23 Goncharov, V.L. 12 14 19 22 186 Gordon, L. 78 164 Goulden, I.P. 5 Gourdon, X. 5 Griffiths, R.C. 85 107 118 Grimmett, G. 7 31 h(n+1) 21 Hald, A. 10 Hall, P.G. 20 186 Hambly, B.M. 26 Hansen, J.C. 4 43 44 103 131 143 171 175 186 Hansen, M.H. 78 Harary, F. 42 Hardy, G.H. 32 36 Harmonic number h(n + 1) 21 81 Hat-check problem 10 Hensley, D. 85 Hildebrand, A. 85 Hirth, U.M. 192 Holst, L. 4 67 190 309 Hoppe, F.M. 119 Hurwitz, W.N. 78 Hwang, H.-K. 5 19 58 133 187 194 Ignatov, T. 110 119 Immigration-death process 227—229 Indicator notation 11 Infinitely divisible 151 154 156 211 236 241 Infinitesimal generator 227 232 Integer partitions 36 Invariance principle, discrete 149 Jackson, D.M. 5 James, G. 56 57 Janson, S. 67 176 190 309 Jaworski, J. 175 Johnson, N.S. 61 Joyal, A. 5 46 47 Joyce, P. 119 Kac, M. 30 Katz, L. 39 Kaufman, G.M. 79 Keevash, P. 26 Kelly, F.P. 4 63 Kerber, A. 56 57 Kerov, S. 119 176 Kingman, J.F.C. 23 108 114 117 175 Knopfmacher, J. 5 45 200 Knuth, D.E. 7 31 32 Kolchin, V.F. 4 14 19 20 22 25 40 43 186 Kolmogorov, distance 226 231 Kolmogorov, three series criterion 203 Kotz, S. 61 Kubilius, fundamental lemma 29 Kubilius, J. 7 29 30 Kurtz, T.G. 103 171 174 Labelle, G. 5 Lagarias, J.C. 45 Landau's formula 29 101 132 Landau, E. 29 101 132 Large deviations 164 Large deviations, fixed number of components 101—103 132—137 Large deviations, number of components 194—199 Large deviations, smallest components 128—130 Large deviations, smallest cycles 22 Leroux, P. 5 Limit distribution 14 Limit theorem, central 19 30 103 Limit theorem, functional 20 30 71—73 103 171—175 Limit theorem, local 19 71 91 101 111 113 127 130 151 152 285 287 Limiting random variable, 80—85 121 126 151 152 230 277—282 Limiting random variable, 82 108 122 152 285 297—298 Limiting random variable, 277—282 Limiting random variable, 85—89 123 127 282—283 Limiting random variable, 86 123 287 297—298 Limiting random variable, 282—283 Lindvall, T. 67 Lloyd, S.P. 4 19 21 22 26 LLT 127—134 138—147 151 176 285 287 298 LLT, definition 127 LLT, sharpening 298 Local limit theorem 71 91 101 111 113 127 130 151 152 285 287 Local limit theorem, permutations 19 Loeve, M. 203 208 214 216 Logarithmic class 51 97 149—160 Logarithmic Condition 2 125—147 152 155 Logarithmic Condition, general statement 65 Loh, W.-L. 225 Lynch, W.C. 61 62 Mahmoud, H.M. 61 Makov, U.E. 61 Markov process 227—229 McCloskey, J.W. 107 119 McGrath, M. 44 Measures of smallness 153—154 Meir, A. 40 Mertens' theorem 34 Metropolis, N. 44 Midzuno, H. 78 Moon, J.W. 40 41 Moser, L. 19 37 Multisets 36 46—47 49—50 55 60 70—73 133 140—143 163 201 222 Multisets, logarithmic 53 70 Mutafciev, L.R. 40 43 175 186 Necklaces 43 Negative binomial, random variables 49 156 Nicolas, J.-L. 25 200 Nijenhuis, A. 36—38 42 Normal approximation 187 O'Connell, N. 26 Odlyzko, A. 5 40 224 Otter, R. 42 p(n) 36 52 Palmer, E.M. 42 Panario, D. 5 22 Partitions, integer 36 Partitions, set 37 Patil, G.P. 119 Pavlov, A.I. 19 25 186 Pavlov, Y.L. 43 Perman, M. 119 permutations 9—27 38 60 95 Permutations, age-ordering 24—25 Permutations, canonical cycle notation 10 Permutations, Cauchy’s formula 11 32 102 Permutations, cycle type 11 60 96 Permutations, distinct cycle lengths 21 Permutations, functional central limit theorem 20 103 Permutations, group order 25 115 199—200 Permutations, limit distribution 14 Permutations, local limit theorem 19 Permutations, longest cycles 22—24 108—115 Permutations, moments 11 Permutations, number of cycles 18 61 100—103 Permutations, number of cycles, Poisson approximation 20 Permutations, ordered cycles 106—107 Permutations, short cycles 96 Permutations, shortest cycles 21—22 100 104—106 Permutations, size-biased 119 Permutations, total variation distance 15—16 Philipp, W. 30 Pitman, J.W. 4 17 37 39 40 43 44 61 119 120 124 Pittel, B.G. 3 4 20 25 37 171 Plouffe, S. 42 Point probabilities, approximation 285—299 Point probabilities, bounds 239—265 Point probabilities, bounds on differences 247—265 Point probabilities, first bound 241 Point probabilities, large argument 243—247 Point probabilities, second bound 243 Point probabilities, successive differences, first bound 249 Point probabilities, successive differences, first uniform bound 253 Point probabilities, successive differences, second bound 256 Point probabilities, successive differences, second uniform bound 262 Point probabilities, successive differences, simplified bound 264 Poisson approximation 20 73—75 186 191 328 Poisson compound 75 151 225—237 Poisson process 14 117—124 229 232 233 Poisson process, coupling 181 182 Poisson process, scale invariant 120—124 180 282 Poisson process, spacings 119 Poisson process, translation invariant 121 Poisson random variables 48 77 126 155 156 225 324 Poisson — Dirichlet approximation 175—186 Poisson — Dirichlet density 23 113 Poisson — Dirichlet distribution 23 115 117—124 Poisson — Dirichlet limit 31 66 73 Poisson — Dirichlet process 73 117—124 192 Population genetics 61 Prime factorizations 27—31 Prime factorizations, conditioning relation 32—34 Prime factorizations, generalized 45 Prime factorizations, Mertens’ theorem 34 Prime factorizations, number of factors 29 201 Prime factorizations, number of factors, asymptotics 29 Prime factorizations, number of factors, central limit theorem 30 Prime factorizations, Poisson — Dirichlet 31 Prime factorizations, size-biased permutation 31 Prime factorizations, total variation distance 29 Prime factors, largest 31 Prime factors, smallest 31 Pure death process 227—229 R(n,c) 46 Rademacher, H. 36 Ramanujan, S. 32 36 Random graphs 38 Random mapping patterns 40 53 186 Random mappings 39 164 186 Random polynomials 43 44 53 163 165 186 200 refinement 53—56 Regular variation 218 Renyi, A. 16 20 30 Residual allocation 119 Revesz, P. 175 217 Richmond, L.B. 5 22 134 Riddell, R.J. 46 Rising factorial 19 Rota, G.-C. 44 S 230 S(N) 154 Sachkov, V.N. 37 Samuels, S.M. 61 Scheffe, H. 115 131 Schmutz, E. 44 143 171 175 187 Schwenk, A.J. 42 Sedgewick, R. 5 Selberg — Delange method 29 Selberg, A. 29 selections 47—48 50—51 55 60 70—73 133 143 Selections, logarithmic 53 70 Set partitions 37 Sevast'yanov, B.A. 4 Shepp, L.A. 4 19 21 22 26 Shmidt, A.A. 23 110 120 Singularity theory 224 Size-biased permutation, cycle lengths of permutations 24 Size-biased permutation, prime factorizations 31 Size-biasing 78—80 83 88 90 91 97 119 139 141 143 144 151 207 223 247 330 Size-biasing, equation 80 125 Size-biasing, Stein analogue 236 Sloane, N.J.A. 42 Slow variation 211 Soria, M. 5 43 44 47 Species 45 Split-merge 119 Stam, A.J. 4 Stanley, R.P. 5 Stark, D. 3 26 29 58 166 170 Stein equation 227 Stein Equation for 231 Stein Equation for 282 Stein Equation for 225 270 291 Stein Operator for 230 Stein Operator for 225 234 270 Stein — Chen method 73—75 190 328 Stein's method 73—75 144—147 151 152 225—237 247 Stein's method for 230—234 277—282 325 Stein's method for 225—230 269—277 Stein, C. 25 73 225 Stepanov, V.E. 40 186 Stirling numbers 18 Stirling numbers, asymptotics 19 Stong, R. 44 Strongly additive 201 subsets 47 Taillie, C. 119 Tavare, S. 3 7 16 21—23 26 43 46 47 61 100 103 104 115 118 123 125 141 143 166 167 170 171 173—175 187 189 191 199 202 Tenenbaum, G. 7 22 27 29 31 85 158 Tilting 57—64 160—163 194—199 Total variation, approximation 226 Total variation, asymptotics 170 Trabb Pardo, L. 7 31 32 Trees 40 41 Trees, search 61—63 Turan, P. 7 25 115 199 Uniform random variables 122 Uniform structures 45 Van de Lune, J. 85 van Lint, J.H. 44 46 Vere-Jones, D. 121 Vershik, A.M. 7 23 110 120 Vervaat, W. 82 85 Vinogradov, A.I. 29 Wasserstein distance 185 Wasserstein distance, bounded 174 187 209 Wattel, E. 85 Watterson, G.A. 4 85 96 109 110 175 Wheeler, F.S. 85 Whittle, P. 4 63 Wieand, K.L. 26 Wilf, H.S. 21 36—38 42 46 Wilson, R.M. 44 46 Wreath products 55 56 Wright, E.M. 36 Wyman, M. 19 37 Yannaros, N. 192 Yor, M. 119 120 124 Zhang, W.-B. 5 45 201 202 211 222 224
Реклама
 |
|
О проекте
|
|
О проекте