Авторизация
Поиск по указателям
Пич А., Лизоркин П.И. (ред.) — Операторные идеалы
Обсудите книгу на научном форуме Нашли опечатку?
Название: Операторные идеалыАвторы: Пич А., Лизоркин П.И. (ред.) Аннотация: Монография известного ненецкого математика, профессора Йенского университета, академика ГДР, посвященная систематическому изложению нового раздела функционального анализа — теории операторных идеалов в банаховых пространствах, в развитие которой большой вклад внес сам автор. Изложение тесно связано с другими разделами математики: спектральной теорией операторов, геометрией банаховых пространств, теорией ядерных локально-выпуклых пространств, теорией случайных процессов. В настоящее издание включен новый материал, полученный от автора. В частности, существенно расширена библиография.
Язык: Рубрика: Математика /Серия: Сделано в холле Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1982Количество страниц: 536Добавлена в каталог: 24.07.2009Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
5.4.1 26.3.1 p-неравенство треугольника (p-triangle inequality) 6.2.1 13.2.6 16.1.7 S-функция (S-function) 11.1.1 13.7.2 s-число (s-number) 11.1.1 13.7.2 Абрамович, Ю.А. 476 484 Абсолютно суммируемое, p-, семейство (absolutely p-summable family) 16.2.1 Абсолютно суммирующий оператор (absolutely summing operator) 6.5.1 Абсолютно суммирующий, 23.1.1 Абсолютно суммирующий, (r,p)-, оператор (absolutely (r,p)-summing operator) 17.2.1 Абсолютно суммирующий, (r,p,q)-, оператор (absolutely (r,p,q)-summing operator) 17.1.1 Абсолютно суммирующий, r-, оператор (absolutely r-summing operator) 17.3.1 Абстрактное C.2.1 Абстрактное C.2.3 Адамара неравенство (Hadamard inequality) 27.2.2 Аддитивная s-функция (additive s-function) 11.8.1 Алгебраическая кратность (algebraic multiplicity) 27.1.3 Аллингер 279 374 484 Амэмия 111 475 476 484 Апёля, Н. 261 474 484 Аппроксимативное число (approximation number)оператора 11.2.1 Аппроксимативное число (approximation number)последовательности 13.7.3 Аппроксимационное свойство (approximation property) 10.1.1 Аппроксимируемый оператор (approximable operator) 1.3.1 Арази 458 484 Ассуад 279 414 484 Аткинсон 414 424 484 Ахиезер, Н.И. 477 Бадрикян 344 401 477 484 Базис (basis) 23.2.3 28.5.1 Банах 477 Банахово пространство (Banach space) A.1.2 Банахово пространство котипа (s,p) (Banach space of (s,p)-cotype) 21.4.11 Банахово пространство радемахеровского типа (s,p) (Banach space of Radamacher (s,p)-type) 21.2.12 Банахово пространство типа (s,p) (Banach space of (s,p)-type) 21.2.12 Баумбах 360 374 484 Баухардт 186 234 300 374 484 485 Бауэр, Н. 477 Безусловно суммирующий оператор (unconditionally summing operator) 1.7.1 Беннетт 344 350 371 373 374 414 484 Берг 477 Беренс, Н. 477 Бессага, С. 90 92 474 479 485 Бидуальное банахово пространство A.24 Бидуальный оператор A.3.6 Бирман, М.Ш. 186 485 Бозами 49 56 458 485 Боненблюст 27 481 Борелевская C.1.8 25.1.1 Борелевская вероятностная мера C.1.8 25.1.2 Борсук 35 Бохнер 401 481 Бохнера интеграл (Bochner integral) 24.1.9 Браун 254 485 Брейс 49 485 Бретаньоль 344 485 Броуновское движение (Brownian motion) 25.6.4 Брудновский, Б.С. 300 474 485 Брэскэмп 425 485 Бурбаки 477 Бургэн 89 92 485 Бутцер 477 Бухвальтер 476 486 Вайдманн 401 486 Вайз 79 82 458 486 Вальдивия 301 486 ван Дюльст 49 490 ван Римсдейк 254 502 Вариация (variation) 24.3.2 Вахания, Н.Н. 478 Вейль, Г. 425 445 481 Вейля тип (Weyl type) 27.4.10 Вейля число (Weyl number) 11.4.4 Вектор-функция 24.1.3 Вектор-функция 24.1.9 Вектор-функция 24.1.2 Вектор-функция (vector function) 24.1.1 Векторная мера 24. 3.4 Векторная мера 24.3.4 Векторная мера (vector measure) 24.3.1 Верон 344 495 Виленкин, Н.Я. 478 Винер 414 482 Винера мера (Wiener probability) 25.6.4 Виттмер 476 486 Вихманн 478 Владимирский, Ю.Н. 48 486 Влока 401 486 Вон, Т.К. 401 486 Вон, Я.-Чж. 478 Вполне непрерывный оператор (completely continuous operator) 1.6.1 Вполне симметричная s-функция 11.7.1 Вполне симметричный квазинормированный операторный идеал 8.2.4 Вполне симметричный операторный идеал 4.4.6 Гантмахер, Ф.Р. 62 69 82 482 Гапайяр 143 476 486 Гарлинг 143 213 254 373 374 414 450 458 476 486 Гарнир 143 478 487 Гауссова мера (Gauss probability) 25.5.2 25.5.3 Гельфанд, И.М. 5 186 401 478 482 Гельфанда число (Gelfand number) 11.5.1 Гёльдера (Hoelder)пространство 22.7.1 Гильберт 39 48 425 482 Гильберта оператор (Hilbert operator) 6.6.1 Гильберта пространство (Hilbert space) D.1.1 Гильберта число (Hilbert number) 11.4.1 Гильберта — Шмидта оператор (Hilbert — Schmidt operator) 15.5.5 Гильберта, 5.4.1 Гиперортогональный базис (hyperonthogonal basis) 23.2.3 Гирлих 8 Глазман, И.М. 477 Глускин, Е.Д. 186 362 363 365 374 401 487 Го 478 Голдберг 478 487 Голдстайн 186 234487 Гордон 143 279 300 320 373 374 382 384 446 453 454 458 486 487 Гохберг, И.Ц. 9 49 82 83 91 186 234 254 424 475 478 487 Гохберга оператор (Gochberg operator) 4.3.5 Грамш 83 92 487 Грибанов, Ю.И. 213 487 Гротендик 8 9 49 66 62—63 82 93 111 134 158 260 261 279 300 356 357 373 385 425 426 445 458 474—476 478 484 488 Гротендика оператор (Grothendieck operator) 3.2.6 Гротендика постоянная (Grothendieck constant) 22.4.5 Гротендика пространственный идеал (Grothendieck space ideal) 29.6.1 Грюнбаум, В. 458 488 Гудмэн 350 373 485 Гулауик 480 Гурарий, В.И. 458 488 Гурса 39 48 482 Густафсон 49 488 Дадли 198 414 488 Дазор 56 300 488 Дакюна-Кастель 115 134 301 320 344 485 488 Данфорд 385 387 401 475 478 482 Данфорда — Петтиса оператор (Dunford — Pettis operator) 3.2.5 Данфорда — Петтиса свойство (Dunford — Pettis property) 3.2.8 Данфорда — Петтиса теорема (Dunford — Pettis theorem) 24.2.3 Данфорда — Петтиса — Филлипса теорема (Dunford — Pettis — Phillips theorem) 24.2. 5 Дворецкий 35 482 488 де Боор 186 485 де Вильде 474 478 486 де Вор 186 485 Дейви 143 158 488 Дейвис 56 234 488 Декартово банахово пространство 2.1.4 Декартово операторный идеал 29.4.1 Декартово произведение банаховых пространств B.4.12 Декартово произведение локально-выпуклых пространств 29.1.10 Декартово произведение операторов 29.1.11 Декартово произведение, C.4.1 Декартово пространственный идеал 29.4.2 Деттвайлер 344 488 Джейн 488 Джонсон, Дж. 458 488 Джонсон, П. 186 489 Джонсон, У. 36 56 90 92 158 234 300 384 440 441 446 453 458 488 489 506 507 Дзоити 279 489 Диканский, А.С. 425 493 Дин 36 143 458 489 Динкуляну 478 Дискретно p-пропускаемый оператор (discretely p-factorable operator) 19.3.11 Дистел 56 62 82 279 401 458 474 478 489 490 Доддс 476 490 Доминационное свойство нормированного операторного идеала 15.4.1 Доминационное свойство нормированного последовательностного идеала 13.8.1 Доминированный, (p,q), оператор ((p,q)-dominated operator) 17.4.1 Доминированный, p-, оператор (p-dominated operator) 17.4.7 Дополняемое подпространство (complemented subspace) B.4.3 Дор 457 458 490 Доран 478 Дробное интегрирование (fractional integration) 22.7.5 Дуализуемый оператор (dualisable operator) 4.4.10 Дуальное банахово пространство A.2.2 Дуальный квазинормированный операторный идеал 8.2.1 Дуальный оператор A.3.5 Дуальный операторный идеал 4.4.1 Дуальный пространственный идеал 4.4.4 Дубински 279 300 384 474 478 490 Дэй 478 Единичное семейство k-e(k-th unit family) A.4.4 Заанен 478 Замкнутый операторный идеал (closed operator ideal) 4.2.4 Замыкание операторного идеала (closure of operator ideal) 4.2.1 Зигмунд 478 Идемпотентная процедура 4.1.2 Идемпотентный квазинормированный операторный идеал 7.1.5 Идемпотентный операторный идеал 3.1.5 Иех 478 Изоморфизм банаховых пространств B.2.1 B.2.2 Изоморфизм локально-выпуклых пространств 29.1.8 Изоморфизм, 26.3.1 Интегральный оператор (integral operator) 6.4.1 Интегральный, 23.3.1 Интегральный, (r,p,q)-, оператор ((r,p,q)-integral operator) 19.1.1 Интегральный, r-, оператор (r-integral operator) 19.2.1 Инъективная s-функция 11.5.4 Инъективная оболочка квазинормированного операторного идеала 8.4.1 Инъективная оболочка операторного идеала 4.6.1 Инъективный квазинормированный операторный идеал 8.4.8 Инъективный операторный идеал 4.6.8 29.3.1 Инъективный пространственный идеал 4.6.8 29.3.2 Инъективный тип C.5.4 Инъекция (injection) B.3.2 Инъекция, 26.6.1 Ионеску, Тулча А. 478 Ионеску, Тулча К. 478 Иосида 39 48 414 424 478 482 Исмагилов, Р.С. 184 186 490 Истрэцеску 279 493 Кавата 479 Кадец, М.И. 279 344 446 450 458 488 490 Кайсер 357 490 Какутани 27 39 48 482 Калкин 82 91 234 ' 482 Калкина алгебра (Calkin algebra) 26.3.4 Кальдерон 213 490 Карл 184 186 198 226 233 234 331 371 373 374 440 446 458 490 491 Карлеман 439 445 482 Картрайт 458 476 491 Като оператор (Kato operator) 1.9.2 Като, М. 279 301 491 497 Като, Т. 39 48 49 425 479 491 Кахан 479 Каханпя 474 491 Качмаж 479 Кашин, Б.С. 184 186 491 Квазидуальное банахово пространство (quasi-dual Banach space) 4.4.9 Квазикомпактный оператор (quasi-compact operator) 26.4.1 Квазинорма на операторном идеале 6.1.1 Квазинорма на последовательностном идеале 13.2.1 Квазинорма на семейственном идеале 16.1.3 Квазинормированный операторный идеал 6.1.3 Квазинормированный последовательностный идеал 13.2.3 Квазинормированный семейственный идеал 16.1.5 Квапень 56 261 265 278 279 320 344 373 374 384 401 413 414 449 458 491 492 507 Кете 56 134 143 213 474 479 482 492 Кёниг 186 234 278 279 330 344 345 359 372—374 440 441 445 446 453 458 476 489 492 Кисляков, С.В. 279 374 401 453 458 487 492 Кларк 374 493 Кляйнекке 49 82 414 424 493 Книс 49 485 Кокрэн 374 479 493 Колмогоров, А.Н. 5 186 198 401 413 479 482 493 Колмогорова число (Kolmogorov number) 11.6.1 Колтон 458 493 Комарчев, И.А. 279 374 493 Компактный оператор (compact operator) 1.4.1 Компактный, (p,q)-, оператор ((p,q)-compact operator) 18.4.1 Компактный, p-, оператор (p-compact operator) 18.3.1 Конечномерная ядерная норма 6.8.1 Конечномерное банахово пространство (finite dimensional Banach space) 2.3.1 Конечномерный оператор (finite operator) B.1.1 Конечномерный подъем 26.1.2 Конечномерный спуск 26.1.3 Константин 234 254 279 493 Коротков, В.Б. 401 493 Коэн 279 458 493 Край 279 493 Красносельский, М.А. 35 479 482 Крачковский, С.Н. 425 493 Крейн, М.Г. 9 35 186 234 254 424 475 478 482 487 Кривин 115 134 301 320 344 356 374 485 488 493 Кхоан, Во-Кхак 300 476 493 Кэрадус 425 479 494 Кюн 300 414 494 Кюрстен 133 134 173 186 222 494 Лапрестэ 279 300 318 320 494 Левин, Б.Я. 479 Левин, В.Л. 476 494 Леворазложимый оператор (left decomposable operator) 24.4.1 24.5.1 Лежаньский 425 445 494 Лей 134 503 Лейси 92 494 Лёфстрём 477 Лиго 476 479 494 Лидский, В.Б. 426 444 445 494 Лизоркин, П.И. 6 7 Линде 300 344 360 374 401 414 458 484 494 495 510 Линденштраусс 35 36 56 89 90 92 158 279 320 344 345 356 373 374 458 479 484 489 495 507 Литтлвуд 38 279 480 482 483 Лифтинга свойство (lifting property) C.3.5 Локально-безусловная структура (local unconditional structure) 23.3.7 Локально-выпуклое пространство 29.1.1 Локально-выпуклый пространственный идеал 29.2.2 Лоренц 186 198 479 495 Лоренца последовательностный идеал (Lorentz sequence ideal) 13.9.1 Лотц, Х. 458 476 479 491 Лотц, Э. 8 Льюис 143 279 300 320 373 374 382 384 446 451 453 454 458 487 495 Люфт 83 92 495 Майер-Ниберг 320 476 495 Майоров, В.Е. 186 496 Мак-Карти 254 458 496 Мак-Фейл 261 458 482 Максимальная s-функция 11.10.1 Максимальная оболочка квазинормированного операторного идеала 8.7.1 Максимальная оболочка квазинормированного последовательностного идеала 13.5.1 Максимальная оболочка операторного идеала 4.9.2 Максимальный квазинормированный операторный идеал 8.7.7 Максимальный квазинормированный последовательностный идеал 13.5.5
Реклама
 |
|
О проекте
|
|
О проекте



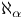 -гильбертов оператор (
-гильбертов оператор ( -изоморфизм (
-изоморфизм ( -, оператор (absolutely
-, оператор (absolutely 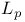 -пространство (abstract
-пространство (abstract 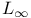 -пространство (abstract
-пространство (abstract  -алгебра
-алгебра -измеримая (
-измеримая ( -
-