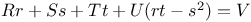|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Пиаджио Г. — Интегрирование дифференциальных уравнений |
|
|
 |
| Предметный указатель |
c-дискриминант 89 90 98 189 237 238 239
p-дискриминант 92—93 94 95 98 152 189 237 238 239
Автор, метод численного приближенного решения 131—135
Адамс 272
Адамс, метод численного приближенного решения 272—275
Алгебра, основные законы 48—49
Ампер 12 223
Ангармоническое отношение частных интегралов уравнения Риккати 246
Ангстрем 78
Асимптотические ряды 265 306
Бернулли, Иоганн 11 24
Бернулли, уравнение 11 32 247
Бернулли, Яков 11 33
Беспроволочная телеграфия 53 64
Бессель 137
Бессель, уравнение 137 141—143 146 148 260 264—265 308
Бессель, функции 137
Бетмэн 270 282
Бибербах 282
Брио и Буке 12
Бродецкий, графический метод 4 18
Бромвич 299
Буль 11
Вада Такео, графический метод 4 12 18 20 21
Вариация параметров 110—113 116
Вейерштрасс, признак равномерной сходимости 161
Возраст земли, вычисление в. з. Кельвином 80 304
Волна, распространение волны в канале с вертикальными стенками 299
Волновая механика 270
Волновое уравнение 267—270
Вращательное движение, устойчивое и неустойчивое 65
Вращение стержня 65
Вронского определитель 307—308
Вспомогательные уравнения 180 199 201
Второго порядка уравнения обыкновенные, в частных производных 70 72 77 78 79 80 81 82 220—225 230 231 232 233 265—271 284 298 299 305 308 310
Второго порядка уравнения обыкновенные, линейные 12 102 106 107 108 109 112 113 114 115 116 136—148 156 254—261 265 306 307 308
Второго порядка уравнения обыкновенные, однородные 104—106
Высших порядков уравнения обыкновенные: в частных производных 211
Высших порядков уравнения обыкновенные: линейные 40 42—43 45 49 52 61 64 65 112—113 114
Высших порядков уравнения обыкновенные: однородные 104
Гамильтон, преобразование 301
Гамильтон, уравнения 301
Гаусс 137
Геометрические задачи, приводящие к дифференциальным уравнениям 33—35
Геометрическое исследование, системы интегральных кривых вблизи особых решений обыкновенного дифференциального уравнения 87—90
Геометрическое исследование, системы интегральных кривых вблизи особых точек 20—21
Геометрическое истолкование линейного уравнения Лагранжа 180
Геометрическое истолкование уравнения Pdx+Qdy+Rdz=0 168—169
Гидростатический маятник 296
Гипергеометрический ряд 115 147
Гипергеометрический ряд, его уравнение 147 148 260
Гипергеометрический ряд, уиттэкерово уравнение г. р. со слившимися особенностями 265
Главные колебания 294 296
Граничные условия 72 76
Графическое изображение интегральных кривых 18—19
Группы преобразований 148 282 342
Группы, непрерывные 12 282
Гурса 12 281—282
Даламбер 11 40 61 67
Дарбу 12
Двойной маятник 295 296
Двойственности принцип 195 196 231 301
Де-ла-Валле Пуссэн, его определение огибающей 235
Действие произвольной системы на связанную с ней простую систему с одной степенью свободы 297
Дискриминант 89—90 92—95 98—99 152 189 236—239
Дифференциал, уравнения в полных дифференциалах 168 178 249—252
Диффузия соли 80—81
Дополнительная функция 44—46 48—50 109 213 310
Жидкость, движение шара в ж. 298
Жидкость, испарение смеси двух ж. 39
Жироскопический эффект 295
Закон Ома для постоянных токов 293
Замена переменных 58 82 99 100 106 114 116 147 148 200
Заострение, место точек з. 90 95 96 237 238
Заряд лейденской банки 44 293
Звук, распространение з. в воздухе от сферического источника 299
Зеемана эффект 296
Инвариант 115
Интеграл Фурье 80
Интеграл, нормальные и субнормальные и. 261—264
Интеграл, общий (уравнения в частных производных) 11 168 180 182—183 192
Интеграл, особый 189—191
Интеграл, полный 186—187 189—194 195
Интеграл, правильный 137 146 254
Интеграл, промежуточный 221 231
Интеграл, решение дифференциального уравнения в форме определенного и. 303—305
Интеграл, специальный 183—184 279—280
Интеграл, частный 11 17 45 50—57 109 213 215 217—218 309
Интегральные уравнения 119
Интегрируемость (см. условия интегрируемости)
Интегрирующий множитель 11 25 30—31 36—37 114 250—251 237 288 311
Исключение параметра из уравнения семейства 88—89 237
Исключение произвольной функции уравнения в частных производных 218—219
Исключение, получение дифференциальных уравнений путем интегрирования произвольных постоянных 14—15 16
Исключение, получение уравнений в частных производных путем интегрирования произвольных постоянных 68—69
Исключение, путем интегрирования произвольных функций 67—68
Испарение смеси двух жидкостей 39
Камертон, его колебания 44
Каноническая форма линейного дифференциального уравнения второго порядка 114 115
Кельвин 78 80 304
Кирхгоф 270
Клейн 12
Клеро 11 97
Клеро, уравнение 11 97—99 100 238 239 242 309
Колебания вынужденные колебания системы, находящейся в резонансе с внешней силой, затухающей вследствие трения 64
Колебания двух связанных электрических цепей 294
Колебания камертона 44
Колебания материальной частицы под влиянием силы, пропорциональной расстоянию, при трении, пропорциональном скорости 44
Колебания мембраны 233
Колебания с неограниченно возрастающей амплитудой 64
Колебания системы под действием внешней периодической силы при сопротивлении, пропорциональном скорости 53
Колебания стержня 232—233
Колебания струны 11 68 81 232 265—266 298
Колебания упругого двойного маятника 295
Колебания, главные 294 296
Колебания, малые 44 294 296 297
Колебания, небольшие к. простого маятника 44 297
Колебания, свободные к. тока 293
Колеблющаяся струна, уравнение 11 68 81 232 265—266 298
Конечные разности 308
Конечные разности, уравнения в к. р. 308—309
Конические сечения софокусные 38 99
Коши 12 149
Коши, метод К. доказательства существования решения дифференциального уравнения 153—154
Кристаль 12
Кристаль, уравнение 184
Кутта, метод численного приближенного решения 130 135
Кэли 11
Лагранж 11 67
Лагранж, линейные уравнения Л. в частных производных 11 180 182—184 193—194 280
Лагранж, метод Л.(вариации параметров) 102 110—113
Лагранж, уравнение 309—310
Лагранж, уравнение движения Л. в обобщенных координатах 301
Лаплас 12
Лаплас, уравнение 70 232 233 270 271 284 305 343
Лежандр 137
Лежандр, уравнение 145 148 260
Лежандр, функция 233
Лейбниц 11
Ли 3 12 282
Линейные уравнения обыкновенные, в конечных разностях 308—309
Линейные уравнения обыкновенные, в частных производных второго порядка 70 72 77 78 79 80 81 82 220—225 230 231 232 233 265 271 284 298 299 305 303 310
Линейные уравнения обыкновенные, в частных производных высших порядков 211
Линейные уравнения обыкновенные, в частных производных первого порядка 68 108 182—184 185—186 193—194 280
Линейные уравнения обыкновенные, в частных производных с постоянными коэффициентами 211—219 304—305
Линейные уравнения обыкновенные, второго порядка 12 102 106 107 108 109 112 113 114 115 116 136—148 156 254—261 265 306 307 308
Линейные уравнения обыкновенные, высших порядков 40 42—43 45 49 52 61 64 65 112—113 114
Линейные уравнения обыкновенные, первого порядка 30—33 307
Линейные уравнения обыкновенные, с постоянными коэффициентами 11 40—66 306—307
Линии тока 38
| Лиувилль, его решение волнового уравнения 268—270
Лобатто 11
Магнитное поле 66
Майер, метод Майера интегрирования уравнения в полных дифференциалах 251—253
Максвелловы уравнения электромагнитного поля 79
Материальная частица, уравнение движения м. ч., притягиваемой силой, пропорциональной расстоянию, при трении, пропорциональном скорости 44
Маятник, гидростатический 296
Маятник, двойной 295 296
Маятник, простой 44 297
Маятник, Фуко 299
Мембрана колеблющаяся 233
Меркурий, неправильность в движении его перигелия 300
Место точек заострения 90 95 96 237 238
Место точек перегиба 243
Место точек прикосновения 94 95 237 238
Место узловых точек 90 96 237 238
Метод автора 131—135
Метод Адамса 272
Метод Бродецкого 4 18
Метод Коши 153—154
Метод Кутта 130 135
Метод Лагранжа 102 110—113
Метод Майера 251—253
Метод Монжа 220—227 230
Метод Пикара 12 117—119 149—152
Метод Пуассона 231
Метод Римса 276—277
Метод Рунге 117 123—129
Метод Сильвестра 237
Метод Фробениуса 136—148 156—162 254
Метод Хойна 130 135
Метод Шарпи 197—200
Метод Якоби 200—203 280—281 301
Метод, символические методы 11 46—64 81—82 211—218 306—307
Митчель 238
Множитель системы 301—303
Множитель, интегрирующий 11 25 30—31 36—37 114 250—251 287 288 311
Множитель, последний м. Якоби 302—303
Множитель, решение системы уравнений с помощью м-лей 165—166
Монж 12 209
Монж, метод М. интегрирования уравнения 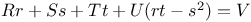 223—227 230 223—227 230
Монж, метод М. интегрирования уравнения Rr+Ss+Tt=V 220—223
Направляющие косинусы касательной к кривой 163
Направляющие косинусы нормали к поверхности 179—180
Начальные условия 17 43 44 71 72
Неинтегрируемые уравнения 174—175
Непосредственное интегрирование 24—39 209—210
Непрерывные группы 12 282
Несущественная особенность 258
Неустойчивое вращательное движение 65
Нормальные интегралы 261—264
Нормальные колебания (см. главные колебания)
Ньютон 11
Общее решение 17
Общий интеграл, обыкновенного дифференциального уравнения (см. общее решение)
Общий интеграл, уравнения в частных производных 11 168 180 182—183 192
Обыкновенная точка 258
Обыкновенные дифференциальные уравнения с тремя переменными 163—178 249—252 279—281
Огибающая 87—88 89 90 93—94 95 96 98 180 189 190 234—236 237 238 239
Однородные уравнения второго порядка 104—106
Однородные уравнения высших порядков 104
Однородные уравнения первого порядка и первой степени 11 26—29
Однородные уравнения, интегрирующий множитель для о. у. в полных дифференциалах 250—251
Однородные уравнения, линейные о. у. в частных производных с постоянными коэффициентами 211—213 305
Однородные уравнения, система линейных однородных уравнений в частных производных 207
Ом, закон О. для постоянных токов 293
Оператор  62 62
Оператор d 46—47 48 50—51 54—56 62 63 108 213 214 306—307
Определенные интегралы, решение дифференциальных уравнений в форме о. и. 303—305
Определитель Вронского 307—308
Определяющее уравнение 136 137—139 140—141 141—143 144—145 146
Орбиты планет 299 300
Ортогональные траектории 11 34—35 38 168—169 232
Основные законы алгебры 48—49
Особенности существенные и несущественные 258
Особое решение 11 17 87—101 234—239
Особые точки 20—21 258—260
Особые точки, регулярная о. т. 258
Особый интеграл 189—191
Падающая цепь 298
Падающее тело, скорость п. т. в воздухе 38
Падающее тело, уравнение движения п. т. в пустоте 107
Параметр, вариация 110—113 116
Параметр, исключение п. из семейства 88—89 237
Педж 282
Первого порядка и первой степени обыкновенные дифференциальные уравнения 24—39 163—178
Первого порядка и первой степени обыкновенные дифференциальные уравнения, линейные 30—33 307
Первого порядка и первой степени обыкновенные дифференциальные уравнения, однородные 11 26—29
Первого порядка и первой степени обыкновенные дифференциальные уравнения, система уравнений 168
Первого порядка и первой степени обыкновенные дифференциальные уравнения, уравнения в частных производных 180—186 193—194
Первого порядка, но более высокой степени, обыкновенные уравнения 83—86
Первого порядка, но более высокой степени, уравнения в частных производных 186—189 197—208
Перегиб, место точек п. 243
Перигелий Меркурия, неправильности в его движении 300
Пикар 11 117
Пикар, метод П. доказательства существования решения дифференциального уравнения 12 117—119 149—152
Пограничные линии 238—239
Подстановки (см. замена переменных)
Поле магнитное 66
Поле электрическое 66
Поле электромагнитное 79
Полные дифференциалы, уравнения в п. д. 168—178 249—252
Полный интеграл 186—187 189—194 195
Понижение порядка уравнения 102 103 106 109
Порядок уравнения 13
Порядок уравнения, его понижение 102 103 106 109
Последний множитель Якоби 302—303
Последовательные приближения 112 117—119 149—152
Постоянные коэфициенты, линейные дифференциальные уравнения с п. к. 11 40—66 306—307
Постоянные коэфициенты, линейные уравнения в конечных разностях с п. к. 309
Постоянные коэфициенты, линейные уравнения в частных производных с п. к. 211—219 304—305
Постоянные, исключение произвольных п. 14 15 16 68—69
Потенциал 38 164 293 299
Потенциал скоростей 299
Потенциал, линии постоянного п. 38
Потенциал, разность 293
Правильные интегралы 137 146 254
Преобразование Гамильтона 301 (см.
Преобразования, группы 148 282
Приближенное решение 299—300 (см.
Прикосновение, место точек п. 94 95 237 238
Принцип двойственности 195 196 231 301
Производная Шварца 115
Произвольные постоянные, исключение 14—15 16 68—69
Произвольные функции, исключение 67—68 218—219
Произвольные функции, определение п. ф. с помощью геометрических условий 209 210
Промежуточный интеграл 221 231
Простое гармоническое движение, его уравнение 14 107 294 296
Простой маятник 44 297
Пуанкарэ 12
Пуассон, метод 231
Пуассон, решение волнового уравнения 268—270
Пуассон, скобки 201
Пуассон, уравнение 270
Равномерная сходимость 152
Равномерная сходимость, признак р. с. Вейерштрасса 161
Радий, уравнение распада 38
Развертывающаяся поверхность 231
Разделение переменных 11 25
Разложение оператора на множители 108 345
Распад радия 38
Распространение волны в канале с вертикальными стенками 299
Распространение звука в воздухе от сферического источника 299
Распространение тепла в одном измерении 70
Распространение тепла в стержне 77 78 79 80
Распространение тепла в твердом теле, простирающемся в бесконечность по всем направлениям 304
Распространение тепла в шаре 77
Регулярная особая точка 258
Резонанс 53 64 295 296 297
Решение, в виде степенного ряда 16 136—148 154—155 156—162
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте