|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Shorack G.R. — Probability for statisticians |
|
|
 |
| Предметный указатель |
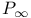 36 36
 -field 3 -field 3
 -field, -field, ![$\mathcal{A} = \sigma[C]$](/math_tex/6b29e9fd3fd1c99732c41746fce0e52a82.gif) 12 12
 -field, -field, 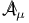 , the completed , the completed  -field 15 -field 15
 -field, -field, 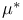 -measurable sets -measurable sets 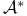 4 4
 -field, histories 305 469 -field, histories 305 469
 -field, induced -field, induced  24 24
 -field, predictable 513 -field, predictable 513
 -field, preservation of 22 -field, preservation of 22
 -field, symmetric 156 -field, symmetric 156
 -field, tail 155 -field, tail 155
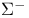 and and 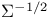 192 379 192 379
A.b.f. 8
Absolute continuity 255 258
Absolute continuity of functions 74 76 78 323
Absolute continuity of log f 78 138
Absolute continuity of measures 60 63 64 66—68 78 108
Absolute continuity of the integral 42 54 66 76 480
Absolute continuity Radon — Nikodym 66
Absolute continuity, fundamental theorem of calculus 76 78 137
Adapted 35 36 305
Added touch 124 268
Ancillary statistic 173
Approximation by continuous functions 59 60
Approximation by elementary functions 26
Approximation by simple functions 26
Approximation by step functions 59 78
Approximation for 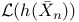 396 396
Approximation lemma, for sets 16 80 155 156
Associated rvs 264
Best linear predictor 194
Bootstrap 274 277 388 432
Bootstrap Bayesian 434
Borel sets 5 6 17 18 23
Borel sets 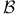 , , 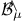 , , 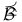 18 18
Borel sets, countable base 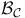 of of 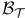 91 91
Borel sets, generators of 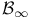 36 86 36 86
Borel sets, generators of 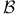 24 24
Borel sets, generators of 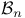 23 35 80 23 35 80
Borel–Cantelli 204 217 218 236 237 244 321 376
Bounded variation 74—76
Bounded variation, total variation measure 62
Branching processes 484
Brownian bridge 202 302 326
Brownian motion 202 235 302 311 318 469 500 536
Brownian motion integrals of 303
Brownian motion LIL 303 320
Brownian motion path properties 323
Brownian motion reflection principle 314 315 321 322 331 409
Brownian motion transformations 303 318
Cantor set 108 114
Caratheodory covering 12 17 77
Caratheodory extension theorem 5 10 12 80 88 480
Censored data 523 527
Chain rule 67 78
Change of variable 78 113 134
Change of variable, Radon–Nikodym 66—68
Change of variable, unconscious statistician 42 67 113
CHF 242 294 341 351
Chf continuity theorem 342 350 351 366 381
Chf distributions on grids 361
Chf examples 343—345 349
Chf expansion for uan array 400
Chf Fourier, Laplace, etc. 341 356
Chf moment expansions 352—354 371 374
Chf tail behavior 355
Chf uniqueness theorem 342 346 347 350 351 366
Chf, complementary pair 346
Chf, empirical 348
Chf, Esseen's lemma 358 371 373 385 391 394
Chf, inversion formula 346—348 359 362 380 381 385 386 393
Chf, multivariate normal 200
Chisquare tests 369 379 389
CLT 125 126 147
CLT for general iid uan arrays 406
CLT, asymptotic normality condition 265 406 529
CLT, basic dependent 529
CLT, Berry–Esseen 259 261 263 267 270 276 278 371 376 450
CLT, Berry–Esseen for U-statistics 454
CLT, bootstrap 274 434
CLT, classical 183 238 342 366
CLT, connection with variance estimation 125 233 270 271
CLT, creating normality 428
CLT, delta method 279
CLT, Doeblin 285 370
CLT, Edgeworth (see also) 391
CLT, examples 279 280 282 283 286 287 368 369
CLT, finite sampling 388 430 464 465
CLT, Frechet — Shohat via moments 293
CLT, gamma approximation 383 388 389 459
CLT, Hoeffding's combinatorial 458
CLT, L-statistics 441 442
CLT, Liapunov 371 377
CLT, Lindeberg — Feller 260 266 267 373 404 529
CLT, local limit (see also) 380
CLT, martingale 530
CLT, multivariate 201 368
CLT, negligibility 215 233 234 367
CLT, Poisson approximation 386
CLT, R-statistics 427
CLT, random sample size 285
CLT, Rebolledo 503 505
CLT, slowly varying 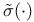 233 268 270—272 233 268 270—272
CLT, Stein's approach 255 262 263 459
CLT, Studentized CLT for 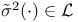 270 272 270 272
CLT, trimmed means 416 417 420
CLT, U-statistics 450 453
CLT, universal bootstrap CLT 277
CLT, universal studentized CLT 276
CLT, Winsorized 264 270
Compensator 487 488 501 511
Complete measure 15 18 29
Complete space 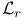 51 51
Completeness assumption 469
Conditional expectation 158 159 168 171 246 248
Conditional expectation, properties of 163
Conditional probability 159 160 186 201
Conditional probability, regular 10 168—170
Contiguity 567
Convergence a.e. 29—31 51
Convergence a.s. 33 78 89 114 241
Convergence almost uniform 60
Convergence in 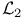 78 78
Convergence in distribution 33 52 89 112 114 241 288 290 291 293 342 531
Convergence in measure 30 31 51
Convergence in probability 33 51 89 241
Convergence in quantile 112
Convergence in rth mean 33 51 89
Convergence in sub-df 288
Convergence modes 57
Convergence set 29 217 242 252
Convergence uniform 60
Convergence, Cesaro summability 205 217
Convergence, DCT 41
Convergence, fd convergence 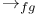 91 91
Convergence, MCT 40
Convergence, mutual 29—31 51
Convex 46 48 49 56 468
Convolution formula 187 347–349
Correlation coefficient 286 463
Correlation coefficient, multiple 194
Correlation coefficient, Spearman 462
Counting process 470 501
Coupling 262 389 542
Cramer — Levy continuity theorem 350
Cramer — von Mises 304 331 338 339
Cramer — Wold device 351 368 378
Cumulant gf 356 371 384 387 388 392
Cumulative hazard function 470 506 522 527
Decomposition of Normals 405
| Decomposition of Poissons 405
Dense in Hilbert space 106
Dense, Bernoulli polynomials 223
Dense, continuous functions 59 78
Dense, step functions 59 78 482
Density estimation 348
Derivative series 71
Derivative under integral sign 45 317
Derivative, differentiable 70 75 76
Derivative, Dini derivates 70
Derivative, Lebesgue theorem 70 71 78
Derivative, Radon — Nikodym 66—68 74 76—78 158
Derivative, Taylor's theorem 72 352
Determining class 347
Determining class limit 53
Determining class moments 293 294 354
Determining class, 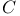 , , 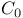 , , 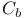 , , 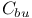 , , 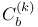 , , 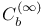 292 292
Determining class, 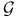 , , 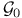 , , 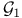 , , 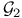 292 292
Determining class, chf 294
df 20 33 107
Df properties 113
Df support 110
Df, absolutely continuous 108
Df, decomposition of 107
Df, generalized 18 19 27
Df, joint 84 85 154
Df, jumps and flat spots 110 134
Df, Lebesgue singular 71 108
Df, singular 108
Df, sub 33 107 288
Diagonalization 289
Discontinuity set 26
Distribution sampling without replacement 180
Distribution, Bernoulli 179
Distribution, Beta 184 549
Distribution, binomial 179 555
Distribution, Cauchy 184 187 242 284 342—344 412
Distribution, chisquare 183
Distribution, compound Poisson 402
Distribution, de la Vallee Poussin 343 346 348 363
Distribution, discrete uniform 555
Distribution, double exponential 184 283 345 558
Distribution, exponential 181 287
Distribution, extreme value 286 559
Distribution, gamma 182 383 392 406 556
Distribution, geometric 179
Distribution, hitting time 409
Distribution, hypergeometric 180 555
Distribution, log gamma 559
Distribution, logistic 184 345 558
Distribution, multinomial 185 369 402
Distribution, multivariate normal 199 286
Distribution, NegBiT 179 387 555
Distribution, noncentral 378 379 389
Distribution, normal 183 287 405 549 556
Distribution, Pareto 562
Distribution, Poisson 181 284 287 386 405 555
Distribution, Snedecor's 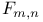 188 557 188 557
Distribution, stable laws (see also) 407
Distribution, Student's 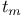 188 557 188 557
Distribution, triangular 343 346 348
Distribution, uniform 184 558
Distribution, Weibull 561
Divergence set 29
Domain of attraction 145
Domain of attraction,  (Normal) 267 268 271 272 277 (Normal) 267 268 271 272 277
Domain of attraction, 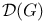 of the stable law of the stable law  407 412 407 412
Domain of attraction, 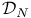 (Normal) 413 (Normal) 413
Domain of attraction, 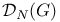 of the stable law of the stable law  407 412 407 412
Domain of attraction, statistical  145 417 442 145 417 442
Domain of attraction, total  145 145
Edgeworth expansions 386 391 392
Eigenvalues 191 196 340
Embedding, Csoergo, Csoergo, Horvath, Mason 328
Embedding, Shorack 328
Embedding, Skorokhod 235 312 318 329
Empirical chf 348
Empirical df 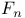 121 223 325 121 223 325
Empirical df 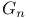 121 223 325 417 121 223 325 417
Empirical finite sampling process 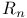 326 326
Empirical process 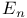 121 121
Empirical process 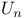 121 325 368 417 121 325 368 417
Empirical qf 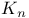 120 120
Empirical quantile process 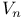 325 325
Empirical two-sample process 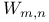 331 331
Empirical weighted process 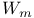 326 326
Equivalent summands 267
Euclidean space 23
Euler's constant 186 546 550
Expectation 38
Expectation of products 152
Extremes 370
Filtration 469 489 493 511
Finite-dimensional convergence projection mappings 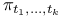 90 90
Finite-dimensional convergence rectangle 86 89
Finite-dimensional convergence subsets 90
Finite-dimensional convergence, 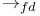 91 91
Finite-dimensional convergence,  -field 90 -field 90
Finite-dimensional convergence, distributions 90
Function,  -function 59 -function 59
Function, elementary 24—26
Function, indicator 3 24
Function, measurable 24
Function, simple 24—26 28 37 166
Function, step 59
Gambler's ruin 499 500
Gamma approximation; the GLT 383
Gamma function 546
Gamma function, digamma 546
Generalized inverse 193
Generators 4
Generators of the induced  24 24
Generators of the induced 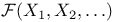 35 35
Generators of the induced 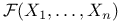 35 35
Generators regarding 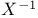 22 22
Generators regarding independence 9
Generators,  -field 3 10 24 -field 3 10 24
Generators, Glivenko — Cantelli 223 325 326
Generators, various for Borel sets 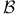 24 24
Generators, various for Borel sets 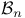 23 35 80 23 35 80
Generators, various for Borel sets 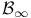 36 86 36 86
Hermite polynomials 317 390 391 470
Hewitt — Savage zero-one law 156
Hilbert space 104 174
Hilbert space, 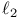 -isomorphism 106 -isomorphism 106
Hilbert space, 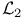 is a Hilbert space 104 is a Hilbert space 104
Hilbert space, alternating projections (ACE) 175
Hilbert space, Fourier coefficients 105 106 340
Hilbert space, Gram–Schmidt 106
Hilbert space, idempotent operator 174
Hilbert space, inequalities 104 106
Hilbert space, orthogonal projections 105 174
Hilbert space, orthonormal basis 105 106
Hilbert space, projection operator 176
Hilbert space, self-adjoint operator 174
Hilbert space, subspaces 105
Hitting time 311 314 409
Hodges — Lehmann estimator 455 456
I.o. 8 204
Increment function 18
Independence tests 369
Independent 163
Independent  -fields 151 153 -fields 151 153
Independent rvs 151 153 154 157 189 200 201 351
Indicator function proof 28 38 42 66 81 83 164 166
Induced distribution 23 24 27 33 42 52 92
Induced distribution consistency 87
Inequality, 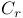 -inequality 47 163 209 313 372 -inequality 47 163 209 313 372
Inequality, basic 49
Inequality, Birnbaum–Marshall 249 333
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



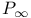
 -field
-field ![$\mathcal{A} = \sigma[C]$](/math_tex/6b29e9fd3fd1c99732c41746fce0e52a82.gif)
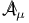 , the completed
, the completed 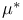 -measurable sets
-measurable sets 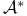

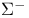 and
and 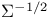
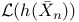
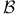 ,
, 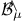 ,
, 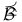
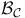 of
of 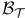
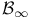
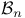
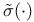
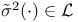
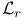
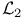
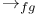
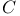 ,
, 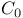 ,
, 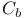 ,
, 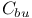 ,
, 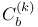 ,
, 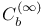
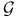 ,
, 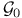 ,
, 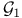 ,
, 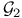
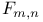
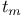
 (Normal)
(Normal) 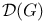 of the stable law
of the stable law 
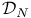 (Normal)
(Normal) 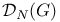 of the stable law
of the stable law 
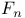
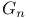
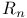
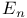
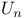
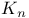
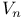
 -function
-function 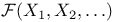
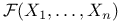
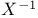
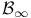
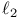 -isomorphism
-isomorphism 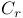 -inequality
-inequality