|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Shorack G.R. — Probability for statisticians |
|
|
 |
| Предметный указатель |
Inequality, Bonferroni 50
Inequality, bounds on 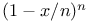 354 550 354 550
Inequality, Cantelli 221
Inequality, Cauchy — Schwarz 48 197
Inequality, Chang 336
Inequality, Chebyshev 49 218
Inequality, chf bound on tails 350
Inequality, chf key inequality 372
Inequality, convexity 48
Inequality, correlation 48
Inequality, Daniels' equality 214 230 335
Inequality, dispersion 167 209
Inequality, Doob 247 249 335
Inequality, Etemadi 212
Inequality, geometric mean 50
Inequality, Gine — Zinn symmetrization 213 273
Inequality, Hajek — Renyi 221 248 333 452 453
Inequality, Hardy 50
Inequality, Hilbert space inequalities 104 106
Inequality, Hoeffding — Frechet 85
Inequality, Hoelder 47 48 163 209
Inequality, Hoffman — Jorgensen 250
Inequality, Jensen 49 163 166 167 209 248 468
Inequality, Khinchin 213 273
Inequality, Kolmogorov 210 217 218 247 248 253 285 321
Inequality, Kolmogorov's other 243
Inequality, Levy 211 220 235
Inequality, Liapunov 48 163 209 371
Inequality, Littlewood 48
Inequality, Markov 49 209
Inequality, Mills' ratio 235 237 321 322
Inequality, Minkowski 49 53 163
Inequality, moment expansions of chfs 352 354 371 374
Inequality, monotone 205 221 247 248 321
Inequality, Ottavani — Skorokhod 212 242
Inequality, Paley–Zygmund 49 273 324
Inequality, Pyke–Shorack 328 334 336
Inequality, sandwiching the mean 206 207 215 217 218
Inequality, Shorack 141 143 147 214 256 458
Inequality, Shorack–Smythe 247
Inequality, symmetrization 210 219
Inequality, truncation 219 227–229 232
Inequality, upcrossing 473
Inequality, Wellner 50
Inequality, Winsorized variance 141 143 147
Inequality, Young 47
Infinitely divisible 400
Infinitely divisible, limits of 400
Infinitely divisible, log chf is never zero 400
Infinitely divisible, subclass  400 400
information 35
Integrable 38
Integrable collection 54
Integrable, 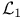 37 37
Integrable, 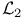 78 78
Integrable, 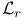 37 47 37 47
Integrable,  37 37
Integrable, product 82
Integrable, uniformly 54—56 221 252 473 477 478 488 492 511 516
integral 38
Integral, improper 44
Integral, Lebesgue 37
Integral, Lebesgue — Stieltjes 44
Integral, linearity 38 163
Integral, Riemann 1 75
Integral, Riemann — Stieltjes 44
Integration by parts formulas 115 118
Inverse image 21 22
Inverse image of  -fields 22 -fields 22
Inverse transformation 111
Jacobian 78 190
Khinchin equivalent rvs 206 207 215 244
Kolmogorov consistency theorem 92 302
Kolmogorov Extension Theorem 87
Kolmogorov inequality (see also) 210
Kolmogorov representation theorem for 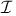 402 402
Kolmogorov zero-one law 155 204 482
Kolmogorov, Gnedenko — Kolmogorov theorem 123 232
Kolmogorov, Kolmogorov — Smirnov 316 331
Kolmogorov, SLLN (see also) 215 275
Kullback — Leibler information 564 567
Large deviations 395
Lebesgue decomposition theorem 64 66 108
Lebesgue integral 37
Lebesgue measure 6 23 38 67
Lebesgue measure 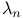 80 80
Lebesgue sets 15 17
Lebesgue singular df 71 108
Lebesgue sums 1
Lebesgue theorem re derivatives 70 71 78
Lebesgue, Lebesgue — Stieltjes measure 4 18 20 77 78 80
Likelihood ratios 470
LIL 235 238 321 323 303 see
LIL, U-statistics 452
Limit determining class 292
Limit theorem, general uan terms 405
Limit theorem, uan terms with negligible variances 403
Lindeberg's 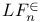 260 266 267 278 283 373 375 376 436 260 266 267 278 283 373 375 376 436
Linear algebra 191
Lipschitz condition 74 540
LLN 126 148 218 222 224—226
LLN, Glivenko — Cantelli (see also) 223
LLN, negligibility 215 226
LLN, random sample size 220
LLN, SLLN of Kolmogorov 208 215 220 275 481
LLN, strong 221 224 238 245 325
LLN, U-statistics 452 453 481
LLN, uniform SLLN of Chung 252
LLN, weak 208 224 226 228 245 366 377 406 425
LLN, WLLN of Feller 208 215 220
LLN, WLLN of Khinchin 208
Local limit theorem 380
Mann — Whitney statistic 456
Martingale 246 311 317 467
Martingale,  notation 246 notation 246
Martingale, closes 473 477 478 493
Martingale, CLT 530
Martingale, convergence theorem 473 477 478
Martingale, counting process 470
Martingale, decomposition 487 488 502 511 512
Martingale, equivalence 246 467
Martingale, examples re empiricals 333
Martingale, exponential 470 499 500
Martingale, integrable 468
Martingale, Kakutani 470 482
Martingale, local 511
Martingale, optional sampling theorem 312 472 492 493
Martingale, reversed 335 453 478 481 498
Martingale, s-mg 246 467
Martingale, square-integrable 468
Martingale, sub mg 246 247 467
Martingale, transform 489 490 502 513 516
Martingale, U-statistic 452
Martingale, Wald 469
Mason theorem 329 332 336
Maximum likelihood 551 563
Measurability criterion 24 25
Measurable 24
Measurable as a limit 25 29
Measurable function spaces 90
Measurable function spaces,  90 295 298 90 295 298
Measurable function spaces,  297 297
Measurable function spaces, 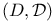 295 298 469 295 298 469
Measurable function spaces, 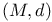 with with  295 295
Measurable function spaces, 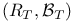 91 91
Measurable function spaces, ![$(R_{[0,1]}, \mathcal{B}_{[0,1]})$](/math_tex/9fcfc008ce1ce8ca50b7f119f0db3d2882.gif) 90 90
Measurable function spaces, general space 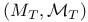 90 90
Measurable partition 37
Measurable set 26 29
Measurable space 3
| Measurable,  -measurable 24 -measurable 24
Measurable, 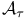 -measurable 306 -measurable 306
Measurable, 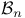 -measurable 84 -measurable 84
Measurable, 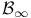 -measurable 86 -measurable 86
Measurable, 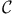 -measurable 298 -measurable 298
Measurable,  -measurable 301 320 -measurable 301 320
Measurable, 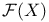 -measurable 24 28 86 158 -measurable 24 28 86 158
Measurable, 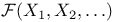 -measurable 35 86 91 -measurable 35 86 91
Measurable, 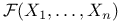 -measurable 35 -measurable 35
Measurable, 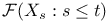 -measurable 36 91 -measurable 36 91
Measurable,  -measurable 239 -measurable 239
Measurable, 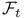 -measurable 36 -measurable 36
Measurable, ![$\sigma[\mathcal{C}]$](/math_tex/f824fb9cd7ed878ce6f50fcddfe4d11582.gif) -measurable 24 28 -measurable 24 28
Measurable, common functions are 25
Measurable, measurability criterion 28
Measurable, non 16 92
Measurable, progressively 306
Measure 4
Measure,  -finite 12 14 61 64 66 80 -finite 12 14 61 64 66 80
Measure, absolute continuity 63 64 66—68 78 108
Measure, Borel 531
Measure, complete 15 18 29
Measure, continuous 7 62 88
Measure, counting 6 67
Measure, finite 61
Measure, induced 23 24 27 33 42 52 92
Measure, Lebesgue 4 6 23 38 67
Measure, Lebesgue 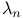 80 80
Measure, Lebesgue — Stieltjes 4 18 20 77 78 80
Measure, monotone property 6 62
Measure, motivation 4
Measure, outer 4
Measure, outer extension 12
Measure, positive part 62 64
Measure, positive set 62
Measure, probability 20
Measure, product 80 81
Measure, regular 16 20
Measure, signed 61 64 66 76
Measure, singular 63 64 71 108
Measure, space 4
Measure, total variation 62 513
Measure, uniform convergence 41 54 60
mesh 44
Metric space 101 295
Metric space, Arzela theorem 103 539 541
Metric space, Ascoli theorem 103
Metric space, compact 102
Metric space, compactness equivalents 102
Metric space, complete 102 537
Metric space, covering numbers 103
Metric space, discontinuity set 26
Metric space, equicontinuity 103
Metric space, equivalent metrics 101
Metric space, properties 101
Metric space, regular measure 16
Metric space, relatively compact 537
Metric space, separable 295 537
Metric space, sup norm 103
Metric space, totally bounded 102
Metric space, uniform continuity 103
Metrics d on 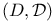 297 297
Metrics, Dudley 540
Metrics, Hellinger 68 543
Metrics, Kolmogorov 543
Metrics, Levy 290
Metrics, Prohorov 540
Metrics, total variation 68 380 543 544
Modulus of continuity 539
moment 46 47 117
Moment, conditional 195
Moment, consistent estimation 226 228 231 270 272 275
Moment, convergence of 53 244 289 293 376
Moment, correlation 48 157 463
Moment, covariance 46 117 157 199
Moment, cumulant 357 388
Moment, generating function 395
Moment, mean 46 116 117 119
Moment, partial 127 128 134 226—228 231 269
Moment, partial variance 145
Moment, skewness 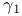 and tail heaviness and tail heaviness 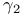 279 357 383 386—388 391 392 554 279 357 383 386—388 391 392 554
Moment, standard deviation 46
Moment, variance 46 116 117 119 233
Moments determine the normal 293
Moments of stable laws 409
Monte Carlo 225
Natural parameters 272
Negligibility 213—215 217—221 226 228 231 233 264 274 275 367 427 430
Negligibility, uan 260 264 283 326 377 399
Nonnegative definite 193 202 363
Norm, 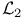 -norm 104 -norm 104
Norm, q-norm 329
Norm, rth mean 46
Norm, sup 22 103 295 330
Null set 15 83
Oh, big 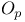 209 209
Oh, big O 9
Oh, little 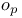 209 209
Oh, little o 9
Oh, o-plus 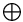 , or “at most” 9 , or “at most” 9
Optional sampling 472 492 499
Order statistics 120 172 173 184 281 325
Orthogonal 104 191 338 339 369 379 512
Partial sum process 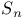 318 319 368 536 539 318 319 368 536 539
Partition 37
PLT 367 404
PLT, negligibility 367
PLT, Poisson limit theorem 367 404
Poisson approximation 386 389
Poisson process 181 470 500
Poisson, compound 402
Poisson, generalized 402
Positive definite 191
Positive part 21 119 468
Predictable 487 489 502 511 513 514 516
Predictable  -field 513 514 -field 513 514
Predictable covariation 512 517
Predictable variation 489 490 501 502 512 516
Probability integral transformation 113
Probability integral transformation, inverse 111
Process 90
Process counting 470
Process realizations (equivalent) 90
Process realizations (smoother) 93
Process,  -class 511 -class 511
Process, convergence on 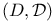 538 538
Process, empirical process (see also) 121
Process, existence of on 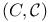 298 298
Process, existence of on 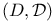 301 301
Process, general 91
Process, increasing 511
Process, independent increments 297
Process, normal 90 202
Process, predicatable (see also) 487
Process, stationary 297
Process, stationary increments 297
Process, versions 90
Product  -field 79 -field 79
Product lemma 353 366 373
Product limit estimator 507
Product measure 80 81
Product null sets 83
Product sections 81 82
Product space 79
Product topology 99
Product, 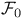 , ,  , , ![$\mathcal{A\times A'} = \sigma[F]$](/math_tex/969c5c470a8ee459bff8c55e554b8d8482.gif) , , 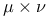 79 79
Product, countable 86
Product, cylinder set 86
Product, Fubini theorem 82
Product, integrable 82
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



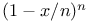

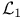
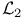
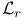

 -fields
-fields 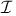
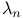
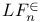
 notation
notation 

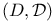
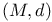 with
with 
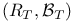
![$(R_{[0,1]}, \mathcal{B}_{[0,1]})$](/math_tex/9fcfc008ce1ce8ca50b7f119f0db3d2882.gif)
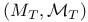
 -measurable
-measurable 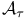 -measurable
-measurable 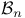 -measurable
-measurable 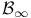 -measurable
-measurable 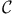 -measurable
-measurable  -measurable
-measurable 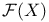 -measurable
-measurable 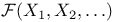 -measurable
-measurable 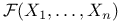 -measurable
-measurable 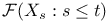 -measurable
-measurable  -measurable
-measurable 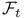 -measurable
-measurable ![$\sigma[\mathcal{C}]$](/math_tex/f824fb9cd7ed878ce6f50fcddfe4d11582.gif) -measurable
-measurable 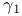 and tail heaviness
and tail heaviness 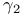
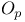
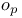
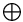 , or “at most”
, or “at most” 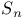
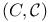
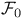 ,
,  ,
, ![$\mathcal{A\times A'} = \sigma[F]$](/math_tex/969c5c470a8ee459bff8c55e554b8d8482.gif) ,
,