|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Salvatore D., Reagle D. Ч Statistics and econometrics |
|
|
 |
| ѕредметный указатель |
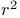 see УDetermination coefficient see УDetermination coefficient
2SLS (two-stage least squares) 230 237Ч238 241
A priori (classical) probability 37 42Ч44 51
A priori theoretical criteria 6
Absolute dispersion 29
Acceptance region in hypothesis testing 87Ч89 95Ч104
Acceptance region in multiple regression analysis 171Ч172
Adjusted 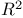 (R, adjusted coefficient of multiple determination) 157 170Ч171 (R, adjusted coefficient of multiple determination) 157 170Ч171
AikakeТs information criteria (AIC) 244 248 253Ч254 261Ч262 265
Almon lag model 183 194Ч196 205
Alternative hypothesis, in hypothesis testing 87Ч89 95Ч96 99Ч101
Alternative hypothesis, in multiple regression analysis 171
Alternative hypothesis, in simple regression analysis 143
Analysis of variance see УANOVAФ
ANOVA (analysis of variance) tables 92Ч93 109Ч115
Arithmetic mean (average) 11
ARMA 242Ч245 249Ч254
Asymptotic unbiasedness 148Ч149
Augmeted Dickey Ч Fuller (ADF) 246Ч247 257
Autocorrelation (serial correlation), and errors in variables 217
Autocorrelation (serial correlation), as problem in regression analysis 208Ч209 215Ч220 242
Autoregression 242 249Ч251
Autoregression function (ACF) 244Ч245 251Ч253
Average (arithmetic mean) 11
Average deviation 13 24Ч25
BayesТ Theorem 39 49Ч50
Behavioral (structural) equations 228 231Ч233
Best linear unbiased estimators see УBLUEФ
Best unbiased (efficient) estimators 133Ч134 147Ч149
Bias 133Ч134 147Ч149 228 231
Biased estimates 147Ч149 183
Biased estimates, and errors in variables 221
Biased estimates, heteroscedasticity and 207
Biased estimates, Koyck lag model and 194
Bimodal distribution 20
Binary choice models 184Ч185 198Ч200
Binomial distribution, as discrete probability distribution 39Ч40 51Ч55 64Ч65
Binomial distribution, in estimation 70 79Ч81
Binomial distribution, in hypothesis testing 88Ч89 90Ч92 98Ч99 105Ч106
Binomial distribution, normal distribution and 60
Binomial distribution, Poisson distribution distinguished from 55Ч56
Binomial probabilities 300Ч305
BLUE (best linear unbiased estimators), in multiple regression analysis 162
BLUE (best linear unbiased estimators), in simple regression analysis 133Ч134 147Ч149
Box Ч Pierce statistic 244 253
Causality 248Ч249 260Ч262 264Ч265
Central tendency 19Ч24 34
Central-limit theorem 68 75 84
ChebyshevТs theorem (inequality) 42 62 66 71 83Ч84 86
Chi-square test, of goodness of fit and independence 90Ч92 104Ч109 120Ч122
Chi-square test, proportions of area of 311Ч312
Class boundaries (exact limits) 18
Class intervals, in descriptive statistics 9 11 16Ч18
Class intervals, in hypothesis testing 106Ч107
Classical (a priori) probability 37 42Ч44 51
cluster sampling 72
Co variance 16 129 145
Cobb Ч Douglas production function 187 210Ч211
Coding 22 27
Coefficients 5Ч7 (see also УSpecific coefficientsФ)
Cointegration 247Ч248 258Ч260 264
Collection of data 2
Collinear independent variable 210
Column (sample) mean 92 109Ч114
Combinations 50
Conditional forecast 197
Conditional probability 38 47Ч48
Confidence intervals, and efficient estimator 147Ч148
Confidence intervals, autocorrelation and 208 216
Confidence intervals, for the mean using t distribution 70Ч71 81Ч84 86
Confidence intervals, in estimation 69Ч70 76Ч81 83Ч85
Confidence intervals, in forecast 183Ч184 197Ч198
Confidence intervals, in multiple regression analysis 165Ч169
Confidence intervals, in simple regression analysis 144
Confidence level, in estimation 69 76Ч80 83Ч85
Confidence level, in forecast 197Ч198
Confidence level, in hypothesis testing 87Ч88 95Ч99
Confidence limits 77
Consistency 148Ч149
Consistent estimators 134 148Ч149 186Ч187
Contingency-table tests 90Ч92
Continuity, correction for 92
Continuous distribution 41 57Ч62 105
Continuous probability distribution 41Ч42 57Ч62 65Ч66
Continuous random variables see УProbability distributionФ
Continuous variables 41 51 57 61
Correlation, coefficient of, in simple regression analysis 132Ч133 132 144Ч147
Correlation, coefficient of, multicollinearity and 210Ч211
Correlation, coefficient of, partial, in multiple regression analysis 158Ч159 172Ч173 179
Correlation, coefficient of, rank 132Ч133 146Ч147
Correlation, coefficient of, simple, in multiple regression analysis 158Ч159
Correlogram 244
Counting techniques 39 50 64
Critical region see УRejection regionФ
Cross-sectional analysis 135
Cross-sectional data 6 213
Cumulative frequency distribution 9 19
Cumulative normal function (probit model) 184 199
Data formats 266 271 292
Deciles 23Ч24
Degrees of freedom heteroscedasticity and 207 213
Degrees of freedom in distributed lag model 193
Degrees of freedom in dummy variable 189Ч190
Degrees of freedom in estimation 70Ч71 81Ч84
Degrees of freedom in forecast 183Ч184 197
Degrees of freedom in hypothesis testing 88 92Ч93 102Ч103 109Ч115
Degrees of freedom in multiple regression analysis 158 171Ч172
Degrees of freedom in simple regression analysis 131 143
delimiters 266 271
Demand function 5Ч7
Density function see УProbability distributionФ
Dependent variable see also УSimultaneous-equations methodsФ
dependent variables 1 3Ч6 44 49
Dependent variables, and errors in variables 221Ч222
Dependent variables, autocorrelation and 216Ч217
Dependent variables, endogenous variable as 228Ч229
Dependent variables, in distribution lag model 193
Dependent variables, in forecasting 197 (see also УForecastingФ)
Dependent variables, in multiple regression analysis 154 (see also УMultiple regression analysisФ)
Dependent variables, in simple regression analysis 128 134Ч136
Dependent variables, multiplication for 38 44Ч49
Dependent variables, qualitative 184 198Ч199
Descriptive statistics 1Ч3 9Ч35
Descriptive statistics, frequency distributions in 9Ч10 16Ч19 33
Descriptive statistics, in multiple regression analysis 157 169Ч171 179
Descriptive statistics, in simple regression analysis 132Ч133 144Ч145
Descriptive statistics, measures of central tendency in 11Ч12 19Ч24 34
Descriptive statistics, measures of dispersion in 13Ч15 24Ч29 35
Descriptive statistics, multicollinearity and 206 210
Determination, coefficient of (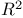 ), and autocorrelation 218 ), and autocorrelation 218
Discrete distribution 17 39Ч40 51Ч57 64Ч65
Discrete random variables 39 51
Disjoint (mutually exclusive) events 37Ч38 44Ч46 63
dispersion 13Ч15 24Ч29 35
Distributed lag models 182Ч183 193Ч196 204Ч205
Distribution curve (ogive) 9 17 19
Distribution, central tendency of 11
Distribution, central tendency of, in simple regression analysis 143 (see also УSpecific distributionsФ)
Disturbance see УError termФ
Double-lag form (model) 181Ч182 186Ч187 202
Double-lag linear model (form) 181Ч182 186Ч189
Dummy variables 182 189Ч193 203Ч204
Durbin two-stage method 217
Durbin-Watson statistic 208 216Ч217 318
Econometric criteria 6Ч7
Econometrics examination 294Ч299
Econometrics, methodology of 1 2 5Ч8
Econometrics, statistics and 1Ч5 7Ч8
Economic theory 1 4
Efficient (best unbiased) estimators 147Ч149 183
| Empirical probability see УRelative frequency distributionФ
Empirical sampling distribution of the mean 74
Endogenous variables 228Ч229
Error correction 247Ч248 258Ч260 264
Error sum of squares (ESS) 110Ч115
Error sum of squares (ESS), heteroscedasticity and 207Ч208 213Ч214
Error sum of squares (ESS), in simple regression analysis 132 144
Error term (stochastic term, disturbance) 1 3Ч6
Error term (stochastic term, disturbance), and errors in variables 209
Error term (stochastic term, disturbance), and qualitative dependent variable 199
Error term (stochastic term, disturbance), autocorrelation and 208Ч209 215Ч220
Error term (stochastic term, disturbance), forecasting errors and 197
Error term (stochastic term, disturbance), in distributed lag model 193Ч194
Error term (stochastic term, disturbance), in multiple regression analysis 165
Error term (stochastic term, disturbance), in recursive models 232Ч233
Error term (stochastic term, disturbance), in simple regression analysis 128 134Ч136 137Ч138
Error term, variance of, and heteroscedasticity 207 212
Errors in variables 209Ч210 221Ч222 226Ч227
ESS see УError sum of squaresФ
Estimate(s), defined 76
Estimate(s), error of the 79 130Ч131 155
Estimate(s), in descriptive statistics 25 27
Estimate(s), in simple regression analysis 128Ч130 (see also УSpecific types of estimates and estimatorsФ)
Estimated demand function 6
Estimated parameters, functional form and 186Ч187
Estimated parameters, in multiple regression analysis 172Ч173
Estimation 1 2 67Ч86
Estimation, confidence intervals for the mean, using t distribution 70Ч71 81Ч84 86
Estimation, indirect least squares 229Ч230 235Ч237 240Ч241
Estimation, sampling 67 71Ч72 84
Estimation, sampling distribution of the mean 67Ч69 72Ч76 84
Estimation, two-stage least squares in 230 237Ч238 241
Estimation, using normal distribution 69Ч70 76Ч81 85
Estimator(s), defined 76
Estimator(s), in multiple regression analysis 154
Estimator(s), in simple regression analysis 140Ч141 (see also УSpecific types of estimates and estimatorsФ)
Eviews 268Ч269 277Ч282 292
Exact limits (class boundaries) 18
Exact linear relationship 128 172Ч173
Exactly identified equations 229Ч230 233Ч235
Exogenous variables 228Ч230
Expected frequencies 90Ч92 104Ч109
Expected value, in binomial distribution 40 51 54Ч55 64
Expected value, of continuous probability distribution 57
Expected value, of error term in simple regression analysis 128
Expected value, of Poisson distribution 55 65
Explained variation (regression sum of squares) 110Ч115 132 144 157
Explanatory variables see УIndependent variablesФ
Exponential distribution 42 61Ч62
F distribution 110
F distribution, heteroscedasticity and 207Ч208
F distribution, in hypothesis testing 92Ч93 109Ч110
F distribution, in multiple regression analysis 158
F ratio 92Ч93 109Ч110 158 171Ч172
F, value of 313
Finite correlation factor 68 73
Finite population 67 73
First-order autocorrelation 208Ч209 215Ч220
Fitting a line 128Ч129 134Ч135
Fixed format 266 271
Forecast-error variance 183Ч184 197Ч198
Forecasting 4 6 7 183Ч184 197Ч198 205
Fourth moment 15
Frequency distributions 1 9Ч10 16Ч19 33 104Ч106
Frequency polygon 1 9 17Ч19
Functional form 181Ч182 186Ч189 202
Gauss Ч Markov theorem 133 148
Geometric mean 11 22Ч23
Goldfield Ч Quandt test for heteroscedasticity 213
Goodness of fit, chi-square test of independence and 90Ч92 104Ч109 120Ч121
Goodness of fit, in hypothesis testing 109
Goodness of fit, in simple regression analysis 132Ч133 144Ч147 153
Grand mean 92 109Ч115
Granger causality 248Ч249 260Ч262 264Ч265
Grouped data 11Ч14 19Ч29 51Ч52
Harmonic mean 11 23
Heteroscedasticity 207Ч208 212Ч215 223Ч225
High multicollinearity 210
histogram 1 9 16Ч19
Homoscedastic disturbances 212
Hypergeometric distribution 40 55
Hypothesis testing 71Ч72 87Ч127
Hypothesis testing, about population mean and proportion 87Ч89 96Ч101 119Ч120 УSimple
Hypothesis testing, analysis of variance in 92Ч93 109Ч115 122
Hypothesis testing, chi-square test of goodness of fit and independence in 90Ч92 104Ч109 120Ч122
Hypothesis testing, defined 1 2 71Ч72 87 95Ч96 119
Hypothesis testing, for differences between two means or proportions 89Ч90 101Ч104 120
Hypothesis testing, overall significance of regression in 171
Identification 229 233Ч235 239Ч240
ILS (indirect least squares) 229Ч230 235Ч237 240Ч241
Income elasticity 140Ч141 175Ч178 181Ч182 187
Inconsistent estimators see УBiased estimatesФ
Independent (explanatory) variables 1 4 6 38
Independent (explanatory) variables, and errors in variables 221Ч222
Independent (explanatory) variables, autocorrelation and 208 216Ч217
Independent (explanatory) variables, binomial and Poisson distributions and 55Ч56
Independent (explanatory) variables, exogenous variables as 228Ч229
Independent (explanatory) variables, heteroscedasticity and 207Ч208 212Ч215
Independent (explanatory) variables, hypothesis testing and 90Ч92 104Ч105
Independent (explanatory) variables, in distributed lag models 193
Independent (explanatory) variables, in forecasting 197 (see also УForecastingФ)
Independent (explanatory) variables, in simple regression analysis 128 134Ч136
Independent (explanatory) variables, lagged 209Ч210 221Ч222
Independent (explanatory) variables, multicollinearity and 206Ч207 210Ч212
Independent (explanatory) variables, multiple regression analysis 154 161
Independent (explanatory) variables, multiplication for 38 44Ч49
Independent (explanatory) variables, qualitative dependent variables and 184
Independent (explanatory) variables, qualitative, dummy variables as 182 189Ч193 203Ч204
Indirect least squares (ILS) 229Ч230 235Ч237 240Ч241
Inductive reasoning 2
Inferential statistics 1Ч3 (see also УEstimationФ УHypothesis
Infinite population 74 84
Instrumental variables 209Ч210 221Ч222
Interquartile range 13 24
Interval estimates 69Ч70 76Ч81
Inverse least squares 222
Joint moment 16
Joint probability 38
Kolmogorov Ч Smirnov test 94Ч95 118Ч119 123
Koyck lag model 183 193Ч194 204
Kruskal Ч Wallis test 94 117Ч118 123
kurtosis 15Ч16 31 35
Lack of bias 147Ч149
Lagged variables 209Ч210 221Ч222
Left-tail test 88 98 102
Leptokurtic curve 15 31
Likelihood function 199
Likelihood ratio index 185Ч186 200
Linear regression analysis 128 134
Linear relationship 154
Log-likelihood function 184 198Ч199
Logistic function (logit) 184Ч185
Logit model (logistic function) 184Ч185 199Ч200
Marginal effect 185 200 205
Mathematics 1 4 7
Matrix notation 159Ч160 173Ч175 179
Maximum likelihood 184 199
Mean absolute deviation (MAD) 13
Mean(s) 11 12
Mean(s), and analysis of variance 92
Mean(s), confidence interval for the, using t distribution 70Ч71 81Ч84 86
Mean(s), hypothesis testing for differences between two proportions or 89Ч90 101Ч104 120
Mean(s), in binomial distribution 39 54Ч55
Mean(s), in descriptive statistics 15Ч16 19Ч24
Mean(s), in normal distribution 41Ч42
Mean(s), in Poisson distribution 40 57Ч58
Mean(s), in simple regression analysis 141Ч142 (see also УEstimation Expected УSpecific
Mean(s), of error term in simple regression analysis 128
Mean(s), of normal distribution as a continuous probability distribution 57Ч58
Mean(s), sampling distribution of the see УSampling distribution of the meanФ
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



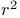
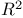 (R, adjusted coefficient of multiple determination)
(R, adjusted coefficient of multiple determination)