|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Wegge-Olsen N.E. — K-Theory and C*-Algebras: a friendly approach |
|
|
 |
| Предметный указатель |
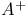 2.1.6f 2.1.6f
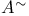 2.1.3 2.1.3
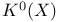 13.3.2 13.3.2
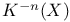 13.3.4 13.3.4
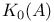 6.2 15.K 6.2 15.K
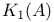 7.1 7.1
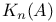 7.2.6 7.2.6
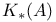 8.B 8.B
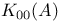 6.2 15.K 6.2 15.K
 -additive functor 11.E -additive functor 11.E
 -unital -unital  -algebra 1.2 -algebra 1.2
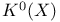 13.3.1 13.3.1
Additive functor 3C 11.1.1
Adjoined unit 1.2 2.1.3
Adjointable operator 15.2.1 15.E
AF-algebras 3.2.3 12.1
Algebraic direct limit L.l
Algebraic tensor product of representations T.5.1 T.5.3
Approximate unit 1.2
Approximation by projections 5.1.6
Atkinson’s theorem 14.1.1 17.1.6
Automorphisms of 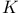 1.10.2 1.10.2
Bases in tensor products T.2.6
BDF-theory 3.G 3.H 3.1
Bott functor 11.1.1
Bott map 9.1.2 9.F 9.1
Bott periodicity 0.2.2 §9 9.J 11.2.1
Bott projection 5.1 7.G 8.F 9.J
Boundedness away from zero 15.G
Busby invariant 3.2.5 3.2.15
C*-equation 1.1
Calkin algebra 14.C
Carl Neumann criterion for invertibility 1.3
Cauchy — Schwarz inequality 15.1.3 15.C
Cech cohomology groups 13.H
Centralizer, double 2.2.6 2.E
Centralizer, double, left, right 2.2.7
Classical Fredholm index §14
Close invertibles 4.2.1
Close invertibles, projections 5.2.6
Close invertibles, unitaries 4.2.4
Cofibre 6.4.6
Cofibre axiom 11.C
Compact adjointable operators 15.2.6
Compact operators 1.5
Compact perturbations 3.G §17
Compactification 2.1.2 2.B 2.C
Complementable Hilbert modules 15.3.1 15.3.9 15.1
Complementable Hilbert modules, ideals 15.J
Cone 6.4.5
Conjugate Hilbert space T.P
Conjugate linear maps T.4.1
Continuity of  6.2.9 6.2.9
Continuity of 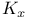 7.1.7 7.1.7
Continuity of tensor maps T.3.8 T.5.19 T.6.9 T.6.23
Continuous functors 11.E 11.1.1
Contractible  -algebra 6.4.1 6.4.4 6.4.7 6.H 11.1.3 16.8 -algebra 6.4.1 6.4.4 6.4.7 6.H 11.1.3 16.8
Corona algebra 2.2.15 10.3
Countably generated Hilbert modules 15.4.7 15.P
Cross norm T.3.2 T.6.21
Cuntz algebras 12.2
Cyclic projection T.5.5f
Decomposition into positive and negative part Appendix O
Deformation retraction 6.4.1
Dimension drop 7.D
Dimension group 12.1.1
Direct limit Appendix L
Direct sum of Hilbert modules 15.1.8
Direct sum of Hilbert modules of  -algebras 2.1.4 2.D 3.2.3 -algebras 2.1.4 2.D 3.2.3
Disorder in  -algebras Appendix O -algebras Appendix O
Double centralizer 2.2.6 2.E
Dual tensor norm T.3.10f T.F
e-Theory 0.2.3
Elementary matrix operations 4.2.8 5.2.14
Elementary tensor T.2.3
Enveloping  -algebra T.L -algebra T.L
Enveloping group Appendix G
EQUIVALENCE 6.4.1 6.4.4
Equivalence of projections 5.2.1
Equivalence of projections of idempotents 5.B
Essential extension 3.2.1
Essential extension, ideal 1.4 2.1.1 2.2.14 15.2.10 T.K
Essential extension, spectrum 3.G
Essentially normal operators 3.G
Exact functor 11.1.1
Exact sequence 3.1.1
Exact sequence of  -algebra tensor products T.6.26 -algebra tensor products T.6.26
Exact sequence of  -algebras 3.1.5 -algebras 3.1.5
Exact sequence of AF-algebras 12.1.1
Exact sequence, long 8.2.1 11.1.4 11.1.12 13.3.4
Exact sequenceof K-groups 6.3.2 7.1.12
Exponential map 9.3.1 9.E
Extension of nuclear  -algebras T.6.27 -algebras T.6.27
Extensions 3.2
Extensions, essential 3.2.1
Extensions, strong equivalence of 3.3.1
Extensions, strong isomorphism of 3.2.13
Extensions, sum of 3.3 3.3.5
Extensions, trivial 3.2.1 3.1
Extensions, weak isomorphism and weak equivalence of 3.E
Fibre of vector bundle 13.1.1
Finite  -algebras 5.F 6.1 -algebras 5.F 6.1
Finite dimensional  -algebras 12.1.2 T.5.20 -algebras 12.1.2 T.5.20
Finite rank operators 1.5
Finitely generated Hilbert modules 15.4
Fredholm alternative 14.A
Fredholm index 0.2.1 8.E §14 17.2
Fredholm matrices 17.2.2
Fredholm operators 14.1
Full Hilbert module 15.1.2
Functional calculus 1.3
Functorial K-theory 11.2.3
Generalized Atkinson’s theorem 17.1.6
Generalized Fredholm index 17.2
Generalized Fredholm operators §17
GNS-construction 1.1 1.5 15.Q
Grothendieck group Appendix G
Half exact functors 3.C 11.1
Half exactness of  6.3.2 6.3.2
Half exactness of 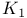 7.1.12 7.1.12
Halving projections 5.3.3ff 7.E 16.4f
Hilbert module 15.1.1 15.1.5
Hilbert module map 15.1.5
Hilbert module, full 15.1.2
Hilbert module, standard 15.1.7
Hilbert space over A 15.1.7
Hilbert — Schmidt operators T.P
Homology functors 11.1
Homology theory 11.1.4
Homotopic, invertibles 4.2.1
Homotopic, morphims 6.4.1
Homotopic, projections 5.2.1 5.D
Homotopic, unitaries 4.2.4
Homotopy 4.2 9.2.9
Homotopy invariance of 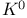 13.3.3 13.3.3
Homotopy invariance of  6.4.3 6.4.3
Homotopy invariance of 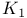 7.1.6 7.1.6
Homotopy invariant functors 11.1.1
Ideal 1.4 1.B
Ideal in tensor products T.6.25 T.K
Ideal, essential 1.4 2.1.1 2.2.14 15.2.10 T.K
Idealizer 2.2.3
Idempotents 5B
Index map in K-theory 8.1.1
Induced vector bundle 13.2
Inductive limits Appendix L 1.4 4.4 T.K
Infinite sums 1.7
Inner product in Hilbert modules 15.1.1
Inner product in Hilbert modules in tensor products T.4 T.G
Irrational rotation algebra 12.3 12.G
| Isometry 5.1.4 5.A
K-functors, surjectivity of 9.H
K-homology 0.2.3
K-idiomatic operations 0.2.2
K-masochist 7.2.3
Kasparov’s stabilization theorem 15.4.6
Kasparov’s technical theorem 2.2.15
KK-theory 0.2.3 3.3.9
Kuiper’s (generalized) theorem 16.8
Kunneth theorem 9.3.3
Laurent loop 9.2.1
Left multiplier 2.F 15.H
Lift of homotopies 4.4.2
Lift of invertibles 4.3.3
Lift of unitaries 4.3.5 17.1.2
Lifting map 3.1.2
Linear loops 9.2.1 9.2.6
Local  -algebras 5.B -algebras 5.B
Locally trivial vector bundle 13.1.4
Long Exact Sequence 8.2.1 11.1.4 11.1.12 13.3.4
Loops in  -algebras 7.2.2 9.2 -algebras 7.2.2 9.2
Loops in topological groups 7.2.2
Loops, Polynomial, Laurent, Projection, Linear 9.2.1
Mapping cone 6.4.5 6.4.8 6.M 6.N 9.G
Mapping cylinder 6.M
Mapping torus 9.K
Matrix algebras 5.C 5.3.6 T.2.13
Maximal  -norm T.6.6ff T.I -norm T.6.6ff T.I
Mayer — Vietoris’ sequence 11.D
Mindex 17.2.1
Mobius strip 13.2.2
Morphisms 1.1
Multiplicative states T.6.11
Multiplier algebras 2.2.2
Multiplier algebras, and tensor products T.6.1 T.N
Multiplier algebras, K-theory for 10.2
Multipliers (left, right, quasi) 2.F
Murray von Neumann equivalence qf projections 5.2.2
Natural transformation 7.2.6 8.A
Neumann criterion for invertibility 1.3
Non-adjointable bounded operator 15.E
Non-commutative topology 1.11 2.A 2.B
Non-degenerate representation 2.2
Non-unital  -algebras 1.2 -algebras 1.2
Norm in Hilbert modules 15.1.5
Normal elements 1.3
Normal Predholm operator 17.2.2
Normalized matrices 4.1.1
Nuclear  -algebras T.6.18ff T.6.26f -algebras T.6.18ff T.6.26f
Nuclear  -algebras, exact sequences of T.2.26 -algebras, exact sequences of T.2.26
Nuclearity of finite dimensional  -algebras T.5.20 -algebras T.5.20
Nuclearity of finite dimensional  -algebras, of commutative -algebras, of commutative  -algebras T.6.20 -algebras T.6.20
Nuclearity of finite dimensional  -algebras, of inductive limits T.M -algebras, of inductive limits T.M
Nuclearity of finite dimensional  -algebras, of multiplier algebras T.N -algebras, of multiplier algebras T.N
Numerical radius T.5.10
One point compactification 2.1.8
Operator algebras 1.5
Ordered group 6.1
Orthogonal complement 5.1.2 15.3.1
Orthogonal direct sum of  -algebras 2.1.4f 2.D 3.2.3 -algebras 2.1.4f 2.D 3.2.3
Orthogonal Hilbert modules 15.3.1
Partial isometry 5.1.4 5.A
Perforation in ordered groups 12.A
Polar decomposition 1.5 l.A 15.3.7f 15.L 17.1.5
Polarization identity 15.1.2
Polygonal homotopy 9.2.9
Portrait of  6.2.7 6.2.7
Positive cone 6.1
Positive elements Appendix O 15.2.5 1.6
Positive elements in abelian groups 6.1
Positive elements, spectrum of 1.3
Positive elements, strictly 15.4.5f
Positive functionals, tensor product of T.B
Positive part of selfadjoint element Appendix O
Powers — Rieffel projection 12.N
Pre-Hilbert module 15.1.1
Product state T.5.7 T.5.11f
Projection loop 9.2.1 9.2.7
Projections 5.1.1
Projections in inductive limits 5.1.7 5.H
Projections, close 5.2.6
Projections, cyclic T.5.5f
Projections, equivalence of 5.2
Projections, halving (or proper) 5.3.3ff 7.E 16.4f
Projections, skew 5.B 15.D
Projections, support/range 5.1.5
Projective modules 15.4.2 15.4.8
Projective plane 5.1
Proper map 2.A
Proper projection see “Halving projection”
Pullback 3.2.6ff 3.D
Pure state T.5.7f T.6.13
PV-sequence 9.3.3 9.K
Pythagoras’ equality 15.B
Quasi multiplier 2.F
Quotient norm 1.4
Quotient space (topological) 13.D
Reasonable tensor norm T.3.12
Reduced K-group 13.3.1
Reduced suspension 13.3.4
Relative K-groups 13.G
Representation 1.5
Representation of Hilbert modules 15.Q
Representation, algebraic T.5.1
Representation, non-degenerate 1.5 2.2
Representation, subcross T.5.3f
Representation, universal 1.5
Representations, Algebraic tensor product of T.5.1 T.5.3
Restriction of multiplicative state T.6.11
Restriction of multiplicative state, of tensor maps T.2.12 T.3.9 T.5.3 T.6.4 T.6.12f
Restriction of multiplicative state, of vector bundles 13.1.4
Riesz group 12.A
Right multiplier 2.F
Ring structure in  6.L 6.L
RIP-group 12.A
Rotation algebra 12.3 12.Gff
Scale of  -algebra 6.1 -algebra 6.1
Scaled ordered group 6.1
Section of vector bundles 13.4
Self dual Hilbert modules 15.1
Similar idempotents 5.B
Simplicity of  -algebra tensor products T.6.25 -algebra tensor products T.6.25
Simplicity of  -algebra tensor products, of rotation algebras 12. J -algebra tensor products, of rotation algebras 12. J
Six term exact sequence 9.3.2
Skew projections 5.B 15.D
Spatial norm, formula for T.5.14 T.5.16
Spatial tensor product T.5
Spectral radius 1.3
Spectral theory 1.3
Spectrum 1.3
Spectrum, essential 3.G
Split exact functor 11.1.1
Split exact sequence 3.1.1
Split exact sequence of  -algebras 3.1.5 -algebras 3.1.5
Split exactness of  and and 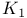 8.2.2 8.2.2
Stability of  6.2.10 6.2.10
Stability of 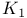 7.1.9 7.1.9
Stabilization 0.2.2 1.10 17.2.2 17.3.2
Stabilization theorem 15.4.6
Stable functor 11.1.1
Stable multiplier algebras 10.3 16.6ff
Stably finite  -algebras 6.1 -algebras 6.1
Standard exact sequence of  -algebras 3.1.5 -algebras 3.1.5
Standard isomorphism 3.3.3
Standard unitary 7.G 9.1 9.J
State T.5.7ff
State, product T.5.7 T.5.11f
State, pure T.5.7f
State, tracial 6.J
State, vector T.5.7 T.5.10f
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



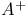
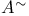
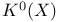
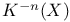
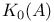
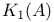
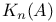
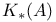
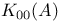
 -additive functor
-additive functor  -algebra
-algebra