|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gilbert J., Murray M. — Clifford Algebras and Dirac Operators in Harmonic Analysis |
|
|
 |
| Предметный указатель |
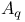 weight 118 weight 118
 functions, analytic over-determinedness of 115 118 functions, analytic over-determinedness of 115 118
 spaces of Clifford analytic functions, and critical index of subharmonicity 242—243 spaces of Clifford analytic functions, and critical index of subharmonicity 242—243
 spaces of Clifford analytic functions, boundary regularity of 242—243 spaces of Clifford analytic functions, boundary regularity of 242—243
 spaces, of Clifford analytic functions in spaces, of Clifford analytic functions in 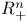 119—125 119—125
 theory, classical 108—119 theory, classical 108—119
 theory, for Clifford analytic functions in a Lipschitz domain in theory, for Clifford analytic functions in a Lipschitz domain in 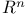 135—141 135—141
 theory, for Lipschitz domains in theory, for Lipschitz domains in 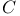 115—119 115—119
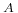 204 204
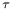 220—232 220—232
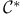 algebra 55 algebra 55
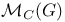 145—146 145—146
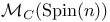 220 220
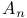 tangential and normal components of, on tangential and normal components of, on 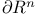 125 125
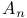 universal Clifford algebra for universal Clifford algebra for 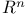 49—65 49—65
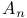 , Banach algebra structure of 53—65 , Banach algebra structure of 53—65
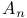 -module 60 -module 60
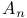 -module, structure of 62—63 -module, structure of 62—63
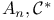 algebra structure of 55—65 algebra structure of 55—65
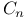 : universal Clifford algebra for : universal Clifford algebra for 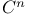 56 56
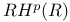 113 113
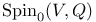 : connected component of Spin(V,Q) 49 : connected component of Spin(V,Q) 49
Adams, J.F. 206 244
Adjoint Dirac operator, 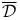 207 207
Ahlfors, L. 318
Algebraically over-determined operator 206
Alvarez-Gaume, L. 318
Analytic over-determinedness 223
Arima, R. 319
Associated vector bundle 266—267
Atiyah — Singer index theorem 244
Atiyah — Singer index theorem, for graded Dirac operators 309—317
Atiyah — Singer index theorem, for spin manifolds 315—316
Atiyah, M. 244 318—319
Axial polynomial 164
Bargmann, V. 284 318
Beardon, A. 85
Bergman space 287—288
Berline, N. 318
Bianchi identities 259
Bismut, J. 318
Bleecker, D. 318
BMO 133
Bochner — Weitzenbock formula 249 258 317
Bochner, S. 199
Booss, B. 318
Boothby, W. 317
Borel — Pompieu theorem 101
Bourguignon, J.-P. 317
Brackx, F. 141
Brauer, R. 94 141
Brocker, T. 85 201
Bruhat decomposition 280
Bruhat decomposition, for 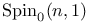 278 278
Burkholder — Gundy — Silverstein theorem, classical 114
Burkholder — Gundy — Silverstein theorem, for 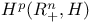 122 122
Calderon — Zygmund type operators 289—290
Calderon, A.P. 126 135 141 239
Capelli 181
Capelli operator 181
Cartan composition 159 222
Cartan — Schur — Weyl theorem 163
Cartan, E. 143 150 163
Cauchy integral operator, for 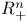 121 121
Cauchy integral operator, for a Lipschitz domain in 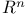 242—243 242—243
Cauchy integral operator, on Tan 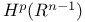 125 125
Cauchy integral theorem, for Clifford analytic functions 101
Cauchy — Binet identity 180 230
Cauchy — Riemann operators 87—93
Cauchy — Szego kernel 293
Cauchy — Szego transform 293 295
Cayley 69
Cayley mapping 70
Cayley operator 180—181
Cayley, A. 181
Chern, S.S. 311
Chevalley, C. 85 181
Class 1 property 164
Class 1 property, for harmonic polynomials of matrix argument 198
Class 1 property, of 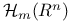 171 171
Clifford algebra 8
Clifford algebra bundle, over a Riemaimian manifold 264 267
Clifford algebra norm 267—268
Clifford algebra, 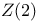 -grading of 14 -grading of 14
Clifford algebra, as a Lie algebra 67—68
Clifford algebra, center of 27—28
Clifford algebra, dimension of 10 11 31
Clifford algebra, even and odd subspaces of 13
Clifford algebra, ideal structure of 28—30 32
Clifford algebra, matrix realizations of 18—22
Clifford algebra, universal 12
Clifford analytic function, definition of 97
Clifford analytic functions, Cauchy integral theorem for 101
Clifford analytic functions, Cauchy theorem for 103
Clifford analytic functions, maximum modulus principle for 104
Clifford analytic functions, Mean-value theorem for 103
Clifford analytic functions, Morera's theorem for 103
Clifford analytic functions, subharmonicity properties of 105—108
Clifford analytic functions, Weierstrass theorem for 104
Clifford group 38 39 42—45
Clifford group, definition of 42
Clifford module 60
Clifford module, structure of 62—63
Clifford norm, on 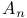 53 267—268 53 267—268
Clifford norm, on 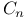 56 56
Clifford operator norm, in 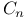 56 128 56 128
Clifford operator norm, on 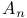 53 53
Clifford semigroup 39
Clifford semigroup, definition of 41
Clifford, W.K. 8 85
Coifman, R.R. 126 134 141 201
Complex Spinor space 151 206
Conformal group 36—38
Conformal map 36
Conformal sphere 37
Conformal transformations 277 281—282
Conjugate Poisson integral 110
Conjugate Poisson kernel 110 121
Conjugation 17 128
Connection 250
Connection, Euclidean 250—251
Connection, Riemannian 251
Covariant derivatives 253
Creation and annihilation operators 15
Critical index of subharmonicity 232—244
Critical index of subharmonicity, defined 233
Curvature operator 254 257
Dahlberg, B. 141
Delanghe, R. 141
Derived representation, on a complex G-module 146
Determined elliptic operator 100
Dilation, of 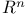 278 278
Dimension, of a Clifford algebra 10 11 31
Dirac 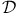 operator 207 operator 207
Dirac operator, basis independence of 95
Dirac operator, standard Euclidean 96
Dirac operators 93—97
Dirac operators, on hyperbolic and spherical space 272—284
Dirac, P.A.M. 83 93 141
Dirichlet problem, for Dirac operator in a Lipschitz domain in 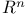 243 243
Dirichlet problem, for Laplace's equation in a Lipschitz domain in 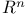 135—137 135—137
Div-curl system 224
Divergence, on a Riemannian manifold 256
Duren, P. 141
Eigenspace representation, of 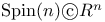 219 219
Elementary symmetric polynomials 69 178
Elliptic operator 205
Equivalence, of first order differential operators 204—205
Equivalent G-modules 144
Equivariant transformation 144
| Euclidean motion group 36
Euler characteristic 311
Euler operator 181
Fatou theorem 110
Fefferman, C. 141
Fiber norm 267
Fischer inner product 164
Flett, T.M. 109
Fourier transform, for 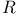 111 111
Fourier transform, for 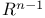 121 121
Freed, D. 317
Friedman, A. 318
Fueter operators 89 92
Fueter, R. 89 140—141
Fundamental representations 147
Fundamental representations, of Spin(n) 159—160 231
G-invariant inner product 145
Garnett, J. 141
Gauss — Bonnet theorem 311 317
Gauss — Weierstrass kernel 297
Gegenbauer polynomials 168 173
Gegenbauer polynomials, of matrix argument 191
Gegenbauer, L. 199
Gelbart, S. 199 201
Generalized Cauchy — Riemann (GCR) operator 206 233
Generalized Cauchy — Riemann (GCR) operator, rotation-invariant 236—237
Generalized Cauchy — Riemann (GCR) system 233
Generalized Cauchy — Riemann (GCR) systems 140
Getzler, E. 248 305 309 317—319
Gilkey, P. 311 318
Goodearl, K.R. 85
Grad, on a Riemannian manifold 255
Graded Dirac operator 97 203 208 210
Graded Dirac operator, determined by an involution 209—213
Graded Dirac operators, rotation-invariance of 216—218
Grassmann 8
Greiner, P. 319
Gross, K. 190
Group of similarities 37
Group representation 144
Hadamard three-circles theorem 109
Hamilton 8
Hardy — Littlewood maximal function 112 122—123
Hardy, G.H. 108
Harish — Chandra 181
harmonic oscillator 297
Harmonic polynomials of matrix argument 193—200
Harvey, F. Reese 85
Heat kernel, existence and uniqueness of 298—301
Heat kernel, of a second order elliptic operator 296—301
Heat kernels, asymptotics for 296—309
Heighest weight, of a representation 150
Helgason, S. 85 201 318
Herz, C. 190 199 201
Higher gradients operators 225 228
Higher gradients operators, critical index of subharmonicity of 239—242
Highest weight submodule 159
Highest weight vector 150—151
Hilbert bundle 267
Hilbert transform for a Lipschitz domain in 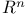 , ,  estimates for 126—135 estimates for 126—135
Hilbert transform, for 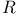 111 111
Hilbert transform, for a Lipschitz domain in 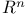 126 242—243 126 242—243
Hilbert — Schmidt inner product 146 204
Hirzebruch signature theorem 317
Hodge deRham 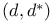 -system 99—100 217—218 222 224 243—244 260 311 -system 99—100 217—218 222 224 243—244 260 311
Hodge laplacian 260 263 307—308 311—312
Hodge-deRham 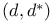 -system, critical index of 237—239 -system, critical index of 237—239
Hodge-deRham 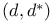 -system, subharmonicity of 237—239 -system, subharmonicity of 237—239
Horizontal lift 269
Horizontal vectors 269
Howe, R. 201
Husemoller, D. 85
Hyperbolic metric 273
Hypergeometric function 168
Hypergeometric function, of matrix argument 190
Imaginary unit 50
Induced representation 286
Injectively elliptic operator 205
Integration by parts theorem 101
Intertwining operator 286—287 290—294
inversion 37 279
Irreducible unitary representation 145—146
Isometry 35
James, A. 201
k-multivectors 50 153 159 262
Kenig, C.E. 115 141 244
Knapp, A. 318
Kobayashi, S. 317
Koornwinder, T. 201
Koosis, P. 141
Koranyi, A. 141
Kostant, B. 201
Kunze, R. 284 318
Laplacian, factorization of 91—93
Laplacian, on a Riemannian manifold 254—255
Laplacian, on a Riemannian manifold, defined 256
Levi, E.E. 299
Lichnerowicz' formula 259
Limits of discrete series representations 288
Linear fractional transformations 275—284
Lipschitz domain, in 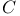 115 115
Lipschitz domain, in 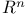 126 126
Lipschitz, R. 72 85
Maas, H. 201 318
Macdonald, I. 201
Marcus, M. 85
Maxwell stress tensor 244
Maxwell's reciprocal theorem 245
Mcintosh, A. 126 141
McKean, H.P. 311 318
Merryfield, K. 290
Meyer, Y. 126 134 141
Minkowski space 6
Moebius group 37—38
Moebius transformation 37
Muckenhoupt, B. 118
Murray, M. 141
Neumann problem, for Laplace's equation in a Lipschitz domain in 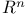 136 136
Nomizu, K. 317
Non-tangential limit 120
Non-tangential limits 110
Non-tangential maximal function 114 122
Norm function 41
Norm function on 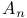 and and 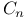 128 128
Normal coordinate system 261
Normalized basis, for a quadratic space 7
O'Meara, O.T. 85
O(n)-harmonic function 194
O(n)-harmonic functions 227
Operator of Dirac type 203
Operator of Dirac type, definition of 208—209
Orthogonal group O(V,Q) 33—38
Orthogonal transformations 32—38
Orthonormal frame bundle 265
Orthonormal frame bundle, oriented 265
Parasarathy, R. 318
Parker, T. 318
Patodi, V. 301 311 318
Pauli matrices 9 25 93
Periodicity theorem, for 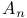 57 57
Pfaffian 72 308
Pfaffian, mapping properties of 72—77
Pim(V,Q) 47
Pin group 47
Pipher, J. 245
Planck's constant 296
Pochhammer symbol 168 190
Poincare group 36
Poisson integral 110
Poisson kernel 110 121
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



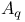 weight
weight  functions, analytic over-determinedness of
functions, analytic over-determinedness of 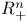
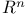
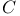
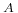
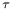
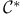 algebra
algebra 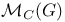
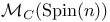
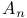 tangential and normal components of, on
tangential and normal components of, on 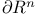
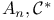 algebra structure of
algebra structure of 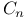 : universal Clifford algebra for
: universal Clifford algebra for 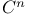
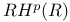
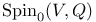 : connected component of Spin(V,Q)
: connected component of Spin(V,Q) 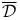
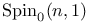
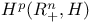
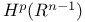
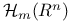
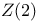 -grading of
-grading of 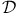 operator
operator 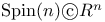
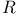
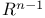
 estimates for
estimates for 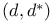 -system
-system