|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Wilansky A. — Modern Methods in Topological Vector Spaces |
|
|
 |
| Предметный указатель |
 complete 193 204 207 216 see 11 complete 193 204 207 216 see 11
 57 57
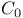 2 see 2 see
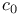 , compact sets 29 106 , compact sets 29 106
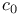 , Hamel basis 9 , Hamel basis 9
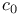 , inclusion and maps 132 147 166 , inclusion and maps 132 147 166
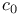 , not dual 32 167 238 , not dual 32 167 238
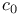 , quotient and subsets 25 29 81 118 230 , quotient and subsets 25 29 81 118 230
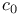 , vs c 29 66 , vs c 29 66
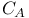 69 199 see 69 199 see
 14 118 14 118
 36 36
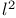 36 81 36 81
 2 22 see 2 22 see
 , ,  251 251
 , basis 144 , basis 144
 , dual 24 , dual 24
 , inclusion 132 253 , inclusion 132 253
 , l 22 , l 22
 , maps 246 , maps 246
 , Mazur 144 , Mazur 144
 , not reflexive 31 230 , not reflexive 31 230
 , not separable 25 144 204 , not separable 25 144 204
 , quasicomplement 239 , quasicomplement 239
 , quotient 257 , quotient 257
 , representation 147 , representation 147
 , subsets 144 145 167 258 , subsets 144 145 167 258
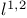 2 see 32 2 see 32
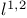 in l 59 in l 59
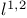 , , 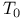 140 140
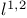 , barrelled 253 , barrelled 253
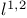 , basis, dual 25 , basis, dual 25
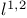 , subsets 26 50 86 , subsets 26 50 86
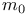 24 251 see 24 251 see
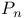 , , 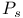 27 29 27 29
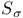 221 223 see 14 221 223 see 14
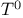 179 183 179 183
 117 153 see 117 153 see
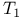 , , 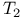 ,etc 10 ,etc 10
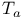 183 183
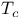 93 97 102 see 2}$"/> 93 97 102 see 2}$"/>
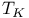 123 133 179 190 see 123 133 179 190 see
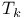 , ,  , ,  155 155
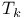 , compatible 134 179 , compatible 134 179
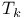 , complete 126 , complete 126
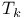 , H-T 126 , H-T 126
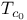 124 179 190 124 179 190
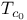 , compatible 134 167 , compatible 134 167
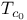 , complete 124 , complete 124
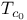 ,H-T 169 ,H-T 169
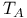 119 see 119 see
 -dual 35 166 -dual 35 166
 152 152
 see Strong; Stone — Cech see Strong; Stone — Cech
 -dual 35 69 -dual 35 69
 200 200
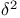 2 123 2 123
 174 174
 -dual 35 36 -dual 35 36
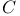 36 98 106 174 see 36 98 106 174 see
 1 1
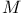 2 57 2 57
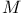 basis 66 basis 66
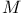 dual 25 dual 25
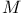 , not locally bounded 55 , not locally bounded 55
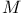 , not normed 25 , not normed 25
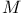 , strictly hypercomplete 200 , strictly hypercomplete 200
 3 see 3 see
 , ,  14 14
 , admissible 122 138 , admissible 122 138
 , BTB 86 , BTB 86
 , dual 24 , dual 24
 , FK 67 , FK 67
 , lc 97 , lc 97
 , map. quotient 199 200 , map. quotient 199 200
 , subsets 18 53 76 90 200 , subsets 18 53 76 90 200
 -barrelled 142 see 17 21 -barrelled 142 see 17 21
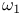 69 71 69 71
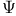 32 32
 38 39 108 see 38 39 108 see
 algebra 238 algebra 238
 , bounded, BTB 49 , bounded, BTB 49
 , compatible 108 , compatible 108
 , complete 73 , complete 73
 , continuous 164 , continuous 164
 , l 39 94 , l 39 94
 , Sup 97 , Sup 97
 , TB 85 , TB 85
 , z 1 56 , z 1 56
 -Stonean 244 247 -Stonean 244 247
 109 133 see esp 109 133 see esp
 3 see 28; 3 see 28;
 , barrelled 221 , barrelled 221
 , basis 9 , basis 9
 , complete 32 , complete 32
 , dual 136 , dual 136
 , in , in 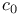 28 28
 , inductive limit 210 , inductive limit 210
 , subsets 9 , subsets 9
 , total 110 , total 110
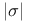 see Normal see Normal
(DF) space 163
(LF) 222 223 see 14
Absolute, 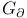 14 14
Absolutely convergent 56 57
Absolutely convex 9 133 135
Absolutely strong 121 138
Absorb(ing) 7 9 113
Additive family 40 92
Adjoint see Dual
Admissible 121 123 see
Affine 265
Alaoglu — Bourbaki 130 154
Algebra 235
Algebraic dual 7 8 35 106 see
Algebraically complementary 61
All subspaces closed 55 110
Almost continuous 201 202
Almost open 57 139 195 196 198 207
Almost range closed 176 177
Amir, D. 29
Analytic functions (see Disc algebra) 57 98
aw* 184 185 190 192 see
b(X), b(X") 150 152 153 161 169 see
B(x, y) 2 28
Baire see First; Second
Balanced 7 see
Banach algebra 71 106 148
Banach limit 25 147
Banach pair 125
Banach space 27
Banach — Alaoglu 130 192
Banach — Dieudonne 191
Banach — Mackey 158 see
Banach — Mazur distance 29
Banach — Saks 32 276
Banach — Sleinhaus closure 34 137 140 see
Barrel 32
Barrelled 136 251 see 8 12 21; Equivalence
Barrelled closed graph 201 205
Barrelled dual pair 125 139
Barrelled inclusion 252
Barrelled not complete 139 249 253
Barrelled open map 195
Barrelled vs quasibarrelled 160
Barycenter 266
Base of 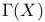 12 see 12 see
Base of 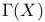 , ,  94 119 94 119
Base of 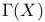 , a.c. balanced open and closed 41 44 93 , a.c. balanced open and closed 41 44 93
Base of 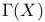 , b(X) 150 , b(X) 150
| Base of 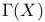 , inductive limit 211 214 , inductive limit 211 214
Base of 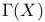 , polar 120 , polar 120
Base of 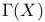 , strong 119 , strong 119
BASIC 66
Basis 64 83 see
Batt, N. 251
Bennelt, G. 252
Berg, I.D. 231
bfa(N), bfa(H, A) 2
BH, BK 67
Bidual 149 162
Biorthogonal 64
Bipolar 112 113
Bornivore 48 50 213 see
Bornological 115 117 see 13 21
Bornological, associated 213
Bornological, dual complete 125 127 188
Bornological, dual pair 125
Bornological, inductive limit 211 212
Bornological, not 116
Bornological, sequentially continuous 116 117
Bounded function 47 see
Bounded function, continuous 21 48 49 116 117
Bounded function, sequentially continuous 47 118
Bounded multiplier summable 251 252
Bounded sets 47 33 95 see
Bounded sets, balanced closure 49
Bounded sets, Cauchy 49
Bounded sets, completion 57
Bounded sets, convex hull 50 86 93 116
Bounded sets, equicontinuous 129 130
Bounded sets, Finite dimension 49 50
Bounded sets, image 47 50 155
Bounded sets, sequential test 47
Bounded sets, strict inductive limit 219
Bounded sets, subspace 49
Bounded sets, sup 48
Boundedly complete 73 139 154 202 see 4 8
BTB space 85 86 88 see
bv 131
BX-, BY-subspace 252
C 242
C(H), 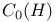 , C*(H) 2 28 29 57 97 98 147 see 3 30;Complement; , C*(H) 2 28 29 57 97 98 147 see 3 30;Complement;
c) 2 see
C* embedded 145
C-barrelled 142 208 see
C-sequential 118 see
Cardinality 66
Category see First; Second
Cauchy see Table 31
Cauchy sequence, net and filter 17 72
Cauchy sup, weak, product 76
Chain 6 55
Characteristic 263
Choquet, G. 265
Closed graph 60 see
Closed graph, converse 205 206 208
Closed graph, lemma 67
Closed graph, separation 217
Closed graph, theorem 60 200 201 203 204 230
Closed graph, X * 203
Closed map 14
Closed set 63 see
Closure 42 see
Closure,  97 97
Closure, bounded 49
Closure, equicontinuous 137
Closure, formula 41 43 44
Closure, sum 42
Closure, [0] 63
Cluster point 227
Cobase 14
Codimension 9 see
Coercive 34 176
Cofinal chain 55
Collecting technique 238
Compact convergence 40 57
Compact map 176 see
Compact set 29 102 155. 22 23;
Compact support 29
Compactification 145
Comparison 14 204 see
Comparison, 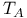 120 120
Comparison,  50 50
Comparison,  97 97
Comparison, bounded sets 47
Comparison, dense sets 106
Comparison, nets 11
Comparison, paranorms 16
Compatible 103 135 see
Complement 62 63 see
Complement, 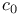 64 147 237 64 147 237
Complement,  63 64 106 237 63 64 106 237
Complement,  200 200
Complement, C(H) 64
Complement, FH 226
Complement, finite dimension and codimension 82 101
Complement, projection 61
Complement, quotient 80
complete 72 16 53 57 see 12;
Complete vs norming 264
Complete, closed graph 63
Complete, comparison 29 59
Complete, dual pair 125
Complete, filter 87 89
Complete, Grothendieck 187
Complete, norm 29
Complete, projection 73
Completely regular 10 13 53 145
Completion 31 57 76 186
Conditionally countably compact 227
conjugate see Dual
Conservative 36 106
Consistent 106
containment 5
continuous see Almost; Bounded function and set; Dual; Hellinger — Toeplitz; Weakly
Continuous addition 37
Continuous FH 65
Continuous inductive limit 210
Continuous multiplication 15 37 44
Continuous net 11
Continuous quotient 77
Continuous semi norm 49
Continuous sup, weak, product 11 13 94
Continuous zeros 54
Conull 36
Convergence 11 see
Convergence,  38 38
Convergence, filter 46
Convergence, Frechet 16
Convergence, lemma 35 189
Convergence, quotient 81
Convergence, sup, weak, product 11 12 13 114
Converse problem 204
Convex 7 9 44 50 76 111 see
Convex compactness 134 see 8 ;Duality
Convex compactness, 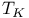 , , 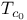 1 34 179 1 34 179
Convex compactness,  135 135
Convex compactness, dual pair 134
Convex compactness, sequentially complete 135
coordinates 64 143
Coregular 36 98 226
Countable: cobase 55 93 152 163
Countable: codimension 222 252 see
Countable: dimension 29 83 see
Countable: inductive limit 212 213
Countable: subsets 49
Countably compact see Table 31; Conditionally;Eberlein — Smulian
Crawford, J.P. 231
CS 2 63 66 132
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 complete
complete 
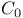
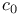 , compact sets
, compact sets 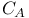


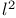


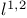
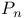 ,
, 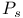
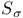
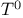

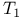 ,
, 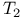 ,etc
,etc 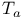
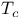
 ,
,  ,
, 
 -dual
-dual 




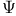

 algebra
algebra 
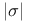
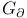
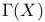
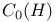 , C*(H)
, C*(H)