|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Wilansky A. — Modern Methods in Topological Vector Spaces |
|
|
 |
| Предметный указатель |
Pettis, B.J. 233 252
Phillips' Lemma 236
Point mass 243 260
Pointwise 33 104
polar 110
Polar family 118 119 120
Polar topology 119 120 123
Probability measure 266
PRODUCT 12 13 39 see Cauchy;Convergence;
Product, absorbing, open 14 50
Product, bornological 265
Product, dual 216 217 218
Product, neighborhoods 14 39
Product, separable 217
Product, subsets 40 217
Product, vs d 217
Projection on factor 12 13 14 76
Projection on subspace 31 see
Projection on subspace, 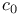 31 147 31 147
Projection on subspace, Third dual 31
Projective limit see 
Properties of a dual pair 125
Pseudomelrizable 10 see
Pseudomelrizable,  97 97
Pseudomelrizable, bornivore 48
Pseudomelrizable, vector space 16
Ptak, V. 193 see
Quasibarrelled 151 see 21
Quasicomplement 63 257 see
Quasinorm 55
Quasireflexive 30 156
Quotient 77 see 2}$"/>;
Quotient, direct sum and inductive limit 211 214
Quotient, inf 81
Quotient, restriction 81
Quotient, semireflexive 155
Quotient, topology 114
Radon measure 224
Radon — Nikodym 239
Raimi, R.A. 159
Range closed 170 197 246 251 258
Range closed, dual map 170
Real vs complex 7
Real-compact 1 18
Reflexive Banach space 30 155 see
Reflexive Banach space, 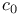 , l 30 230 , l 30 230
Reflexive Banach space, compatible, dual 31 108
Reflexive Banach space, disc 31
Reflexive Banach space, weak* 104 105
Reflexive Ic space 153 see ;Semireflexive
Regular 10 42 see
Relative topology 49
Relative topology,  , ,  , Weak 105 109 , Weak 105 109
Relative topology, compact, equicontinuous 143 180 183
Relatively: compact 130
Relatively: strong 109 see 21
Representation 63 81 see
Restriction 7 see
Restrictive 263
Reversible 69 98 see Right
Riemann — Lebesgue 35
Riesz representation 26
Right inverse 63 71
Robertson, W. 199
Row-finite 69 see
Same see Tables 22 25
Saturated: family and hull 120 123
Saturated: subspace 81
SCC 167 192
Schatz, J.A. 9
Schauder, J. 64 see
Schur, I. 4 237
Scminorm 18 81
Second category 10 29 60 see 7;
Second dual see Bidual
Seever, G.L. 253
Semibornological 126 see
Semiconservative 131
Semifredholm 177 231
Semimontel 90
Seminormed space 18 see
Semireflexive 153 155 199 see
Separable 25 143 see Duality
Separable quotient 208 254—258 see
Separable,  71 71
Separable, admissible 144
Separable, dual pair 125 144
Separable, extreme points 235
Separable, in  144 144
Separable, no basis 66 147
Separated 42 95
Separating 39
Separation 101 102
Separation axioms 10 82
SEQUENTIAL 117 131 see
Sequentially barrelled 142 161 189 see
Sequentially closed: 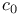 and C[0,1] 117 and C[0,1] 117
Sequentially closed: aw*, weak* 189 192
Sequentially closed: bounded 145
Sequentially closed: dense 138
Sequentially compact see Weak*
Sequentially compact, closed graph 257
Sequentially compact, Eberlein — Smulian 229
Sequentially compact, Mazur 230
Sequentially complete 72 see 4 18 29 30;Boundedly;
Sequentially: continuous 47 93 118 see
Sequentially: dense 155
Sequentially: open 117
| sgn 2
Shirai, T. 224
Silverman — Toeplitz 36 188
SIMPLE 24 240
Small 84 260
Smaller see Minimal
Smaller Frechet 102
Smaller norm 60 118 192
Smallest topology 40 see
Snyder, A.K. 258
Sobczyk, A. 146
Solid 36 123
span 7
Spectrum 146
Stone — Cech 145 146
Stone, M.H. 146 244
Strict inductive limit 218—224 see
Strict topology 265
Strictly 16 101
Strictly hypercomplete 191 192 see 12 21
Strong dual 149 see 19
Strong topology 119
Strong* see Base
Strong, bounded 133 157 see
Stronger 16 see
Subserics 251 252
Sum of subsets 43 82 89 226 264 see
Summability see Banach — Saks;  ; Coercive; FH Matrix; ; Coercive; FH Matrix; 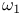 ; Reversible; Semionservative ; Silverman — Toeplitz;Tauberian; Unbounded ; Reversible; Semionservative ; Silverman — Toeplitz;Tauberian; Unbounded
Sup norm 2
Sup of paranorms 18
Sup topology 11 see
Sup topology, 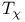 123 123
Sup topology, BTB 85
Sup topology, complete 76
Sup topology, dual 96 98
Sup topology, product 14
Sup topology, smallest 13
Sup topology, TVS 38 97
Sup topology, weak 106
Support 29
t 117 118 265
Tauberian 175 231
Test functions 222 see 28
Test topology 209
Topoloay of uniform convenience see 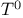
Topoloay of uniform convenience, 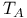 120 120
Topoloay of uniform convenience, bounded see b(X)
Topoloay of uniform convenience, complete 178
Topoloay of uniform convenience, equicontinuous 129
Topoloay of uniform convenience, on 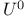 121 121
Topological see Divisors of 0
Topological vector space 37
Topologically complete 14 55
total 18 31
Total dual 95
Total fundamental 104 112
Totally bounded 83—86 89 190 see 31
Two-norm 265
Tychonoff, A. 89
Type M 98
Ulam, S. 265
Ultrabanelled 140 see
Ultrafiltcr 87—89
Unbounded sequences 140 141
Uniform boundedness 33 114 137 157 159 see
Uniformly: bounded 33 35 142
Uniformly: continuous 17
Uniformly: convergent 14 29 see
Uniqueness 59 70 202 203 221 see
Unit disc see Disc
Universal see Embedding l
Unrestricted inductive limit 210
Variation 235
Vecch, W.A. 146
Vector topology 37 45
Voight,.!. 251
Von Neumann. J. 90
w 12 13 38 39
Weak(ly) 12 97 131 see Relative s
Weak(ly) basis 66 141
Weak(ly) compact map 174—177
Weak(ly) compact set 106 167 229 233 240 247
Weak(ly) compactly generated 256—258
Weak(ly) compatible 103 108
Weak(ly) complete 113 see 11
Weak(ly) continuous 168 169 201 206
Weak(ly) metric, norm 104 109
Weak(ly) quotient 114
Weak(ly) sequential closure 113
Weak(ly) sequentially complete 132 see
Weak(ly) sup 106
Weak* 104 105 see
Weak*, bounded 137 see
Weak*, boundedly complete 138 139
Weak*, closed see (Semi-) reflexive
Weak*, compact 130
Weak*, continuous 104 105
Weak*, convergence 35 189
Weak*, dual 104
Weak*, metrizable 106
Weak*, product, pointwise 104 106
Weak*, sequentially compact 230 231 257
Weak*, sequentially complete 139 160 203 see 30
Weaker 16
Webb, J.H. 193
Webs 200
Weston, J.D. 253
Whitley, R.J. 231
zeros 7 9 54 226 249 see
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



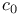

 , Weak
, Weak 

 ; Coercive; FH Matrix;
; Coercive; FH Matrix; 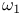 ; Reversible; Semionservative ; Silverman — Toeplitz;Tauberian; Unbounded
; Reversible; Semionservative ; Silverman — Toeplitz;Tauberian; Unbounded