|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Oprea J. — Differential Geometry and Its Applications |
|
|
 |
| Предметный указатель |
Action integral 265
Agnesi 12
Alexandrov's Theorem 142
Analytic continuation 236
Arclength 4 43
Arclength, minimization 255 264 273
Area-minimizing 136—139 334
Area-minimizing, versus Enneper 248—249
Area-minimizing, versus Enneper, in Maple 251—253
Area-minimizing, via Pontryagin maximum principle 299
Astroid 10
Astroid, evolute of 35
Asymptotic curve 132
Bernstein's theorem 235
Bianchi identities 338
Binormal B 20
Bjorling's Problem 235—242
Bonnet's theorem 218
Brachistrochone 261—263 273
Catenary 13 139
Catenary, as solution to variational problem 283
Catenary, evolute of 34 46
Catenoid 59 139 182
Catenoid, as least area revolution surface 264
Catenoid, as least area revolution surface, via Pontryagin maximum principle 299
Catenoid, as minimal surface of revolution 114
Catenoid, as solution to Bjorling's problem 242
Catenoid, Gauss curvature of 101
Catenoid, mean curvature of 101
Catenoid, principal curvatures of 101
Catenoid, Weierstrass — Enneper Rep. of 228 231
Cauchy — Riemann equations 220
Cauchy — Schwarz inequality see Schwarz's Inequality
Characterization of all umbilic surface 109
Characterization of Christoffel symbols by metric 327
Characterization of circle 25
Characterization of circular helices 37
Characterization of conformal Gauss maps 232
Characterization of constant H surfaces of revolution 115—119
Characterization of constant H surfaces of revolution, as roulettes of conies 119
Characterization of constant K surface 104 112
Characterization of curves by curvature and torsion 38
Characterization of curves by curvature and torsion, in Maple see recreate3dview
Characterization of cylindrical helices 35
Characterization of extremals of surface area with fixed volume 293—294
Characterization of line 4 24
Characterization of line of curvature 81
Characterization of meridians and parallels as geodesies 161
Characterization of minimal surface of revolution 114
Characterization of minimal surface of revolution, as solution to Bjorling's problem 242
Characterization of nonarea minimizing minimal surfaces 245—246
Characterization of plane by shape operator 72
Characterization of plane curve 24
Characterization of plane curve in Maple see recreate
Characterization of ruled minimal surfaces 132
Characterization of spherical curves 27 50
Characterization of tangent vector in 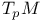 65 65
Christoffel symbols 106 327
Christoffel symbols, vanishing for 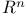 327 327
circle 8 25
Circle, as solution to isoperimetric problem 283
Clairaut parameterization 160
Clairaut relation 159 163—164
Clairaut relation and D’ Alembert's principle 164
Codazzi — Mainardi equations 108
Complex differentiation 219—220
Complex integration 221
complex numbers 219
Cone 62 97—98
Cone, lassoing 179
Cone, unrolling as isometry 179
Conformal map 182
Conformal map, Gauss map on minimal surface 232
Conformal metric 168 291
Conjugate point 214—216
Connection 1—forms 352
Conservation of energy 265—266 289
Contraction 340—341
Contraction of metric 341
Contraction of Ricci 340
Coordinate patch (chart) 54 312
Covariant derivative 70—71 192 318
Covariant derivative of tensor R 338
Covariant derivative, properties 193 318
Cross product 19—20
Cross product in Maple 40
Curvature geodesic 151 172
Curvature geodesic, formula for 173 195
Curvature mechanical 292
Curvature normal 79—80 151
Curvature of a curve k 19
Curvature of a curve k and road banking 30
Curvature of a curve k in Maple 41
Curvature of a noriunit speed curve 28—30
Curvature of a noriunit speed curve, of involute 32
Curvature principal 81
Curvature Ricci 340
Curvature Riemann 335—336
Curvature scalar 340
Curvature sectional 337
Curvature sectional of sphere 337
Curvature, Gauss K 87 105 168
Curvature, Gauss K, constant 102—104 112
Curvature, Gauss K, in Maple 121
Curvature, line of 81 93 94
Curvature, mean H 87 325
Curvature, mean H in Maple 121
Curve 1
Curve asymptotic 132
Curve Newton's 3
Curve of constant precession 23 51—52
Curve parameter 53
Curve speed of 3
Curve spherical 27 50—51
Curve spherical, total torsion of 80
Curve, parameterized line 1
Curve, velocity vector of 1—2
Cusp 16
Cycloid 9—10
Cycloid, as brachistrochone 263
Cycloid, as tautochrone 10
Cylinder 62 82 97—98
Cylinder, shape operator of 72
Cylinder, unrolling 180
Cylinder, versus Enneper in area 248—249
Cylinder, versus Enneper in area, in Maple 251—253
Darboux vector 22—23 37
delaunay see surface
Derivative mapping 76—77
Developable surface 98
Developable surface and lines of curvature 98
Developable surface, tangent developable 98
Direction vector of line 2
Directional derivative 69
Divergence 141 346
Divergence of metric 347
Divergence, Theorem 141
Dot product 5 167
Dot product in Maple 40
D’Alembert's principle 164 284
Eigenvalue 74
Eigenvalue and determinant 74
Eigenvalue and trace 74
Eigenvector 74
Einstein curvature G 345 349—350
Einstein manifold 349
Elastic rod 282
ellipse 15 17 31
Ellipse, evolute of 34
Ellipse, in Maple 45
| Enneper's surface 61 85 229
Enneper's surface, curvatures of 93
Enneper's surface, non area minimizing 248—249
Enneper's surface, non area minimizing, in Maple 251—253
Euler characteristic 205
Euler characteristic, formula for plane 206
Euler — Lagrange equations 257 280
Euler — Lagrange equations two-function 257—258
Euler — Lagrange equations two-variable 258
Euler — Lagrange equations, in Maple 300—304
Euler — Lagrange equations, independence from t 259
Euler — Lagrange equations, with undetermined endpoint 260
Euler, formula of 84
Euler, formula of and mean curvature 90
Euler, spiral of 38
Euler, spiral of and minimizing bending energy 281
Evolute 32 37 45
Evolute of astroid 35
Evolute of astroid in Maple 46
Evolute of catenary 34 46
Evolute of ellipse 34
Evolute of ellipse in Maple 45
Evolute of parabola 33
Extremal 257 267
Fixed endpoint problem 255
Flat 90 115 336
Flat, surface 90
Flat, torus 171
Forms 351
Foucault's pendulum 198—200
Foucault's pendulum, as parallel vector field 199
Frame 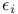 191 195 339 352 191 195 339 352
Frame 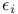 dual 352 356 dual 352 356
Frenet formulas 21
Frenet formulas for nonunit speed curves 28
Frenet frame 20
Gauss map 77—78
Gauss map and area minimization 246
Gauss map and Gauss curvature 90
Gauss map and shape operator 77—78
Gauss map, as meromorphic function 233
Gauss map, conformality of 183 232
Gauss — Bonnet Theorem global 205
Gauss — Bonnet Theorem local 203 214
Gauss(ian) curvature 87 336
Gauss(ian) curvature and compactness 112
Gauss(ian) curvature and Gauss map 90
Gauss(ian) curvature and Jacobi equation 212
Gauss(ian) curvature and second derivative test 98—99
Gauss(ian) curvature and shape operator 88—89
Gauss(ian) curvature from Weierstrass — Enneper Rep. 231
Gauss(ian) curvature in Maple 121
Gauss(ian) curvature of a surface of revolution 100
Gauss(ian) curvature of Enneper's surface 93
Gauss(ian) curvature of hyperboloid of two sheets 95—96
Gauss(ian) curvature of ruled surface 97
Gauss(ian) curvature of sphere 91 95 108 357
Gauss(ian) curvature of torus 100—101
Gauss(ian) curvature, formula for 89 91 105 168
Gauss(ian) curvature, from dual 1-form frame 356
Gauss(ian) curvature, metric formula for 105
Gauss(ian) curvature, Theorem Egregium 105
Gauss(ian) curvature, total, and holonomy 190—191 197
Geodesic 151 192
Geodesic and Maple 185—186
Geodesic and Pontryagin's maximum principle 297—298
Geodesic closed, as periodic orbit 292
Geodesic curvature 151 172
Geodesic curvature, formula for 173 195
Geodesic equations 156 185 329
Geodesic equations, as Euler — Lagrange equations 288 330
Geodesic equations, for Clairaut patch 160
Geodesic of Poincare and hyperbolic planes 181
Geodesic on cone 163
Geodesic on cylinder 154 156
Geodesic on hyperbolic plane 175
Geodesic on hyperboloid of one sheet 165
Geodesic on paraboloid 165
Geodesic on Poincare plane 174 187
Geodesic on sphere 153—154 157
Geodesic on stereographic sphere 176
Geodesic on torus 159 186
Geodesic on whirling witch of Agnesi 163 186
Geodesic torsion 195
Geodesic, as equation of motion 286
Geodesic, as equation of motion in Maple 306—307
Geodesic, as equation of motion with conformal metric 291
Geodesic, as line of curvature 154
Geodesic, as shortest distance 155 288
Geodesic, as shortest distance, detected by Jacobi equation 217 275
Geodesic, existence and uniqueness of 157
Geodesic, invariant under isometry 180
Geodesic, polar coordinates 155 209
Geodesically complete 166 217
Green's theorem 129 138 140 201
Hamilton's principle 265 286
Hamiltonian 296
Harmonic function 146
Harmonic function, as Euler — Lagrange equation 265
Helicoid 60 97 178 182
Helicoid, Weierstrass — Enneper Rep. of 228
Helix 12 18 24 42
Helix circular 37
Helix cylindrical 35
Helix hyperbolic 32
Hilbert's invariant integral 269
Hilbert's invariant integral, independence of path of 269—271
Hilbert's Lemma 114
Holomorphic 219
Holonomic constraints 284
Holonomy 195
Holonomy along latitude of sphere 196
Holonomy along parallel of cone 198
Holonomy and Foucault's pendulum 198—200
Holonomy on Poincare plane 201
Holonomy, as total Gauss curvature 197
Hyperboloid of one sheet 63
Hyperboloid of one sheet, closed geodesies on 165 207
Hyperboloid of one sheet, Gauss curvature of 97
Hyperboloid of two sheets 95
Hyperboloid of two sheets and Bonnet's theorem 218
Hyperboloid of two sheets Gauss curvature of 96
Hypersurface 317 342
Identity Theorem 236
Inner product 167—168
Involute 17—18 44
Involute, curvature of 32
Isometry 177
Isometry global 178
Isometry local 177
Isometry unrolling a cone 179
Isoperimetric problem 283—284
Isoperimetric problem, Euler — Lagrange equation for 283
Isothermal coordinates 148
Isothermal coordinates, existence of on minimal surfaces 222
Jacobi equation 212 216 275
Jacobi equation on sphere 216
Jacobi equation, as Euler — Lagrange equation 275—277
Jacobi's theorem 291
Jacobian 77 316
Jacobian of sphere 316—317
kinetic energy 255 265 284
Kuen's surface 97
Lagrange's identity 19 89
Laplace — Young equation 127
Lie bracket 319
Lie group 344
Liebmann's Theorem 112
Line 1—3 150
Line of curvature 81 93 94
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте