Авторизация
Поиск по указателям
Ahlfors L.V. — Complex analysis
Обсудите книгу на научном форуме Нашли опечатку?
Название: Complex analysisАвтор: Ahlfors L.V. Аннотация: A standard source of information of functions of one complex variable, this text has retained its wide popularity in this field by being consistently rigorous without becoming needlessly concerned with advanced or overspecialized material. Difficult points have been clarified, the book has been reviewed for accuracy, and notations and terminology have been modernized. Chapter 2, Complex Functions, features a brief section on the change of length and area under conformal mapping, and much of Chapter 8, Global-Analytic Functions, has been rewritten in order to introduce readers to the terminology of germs and sheaves while still emphasizing that classical concepts are the backbone of the theory. Chapter 4, Complex Integration, now includes a new and simpler proof of the general form of Cauchy's theorem. There is a short section on the Riemann zeta function, showing the use of residues in a more exciting situation than in the computation of definite integrals.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: second editionГод издания: 1966Количество страниц: 317Добавлена в каталог: 18.05.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
46 264—269 Abel limit theorem 42 Abel power series theorem 39 Absolute convergence 36 Absolute value 6—8 Accessory parameter 229 Accumulation point 53 Addition theorem 43 Algebraic curve 297 Algebraic function 291—297 Algebraic singularity 290 Amplitude 13 Analytic arc 226 Analytic continuation 170 275—290 Analytic function see Function angle 14 84 Apollonius 84 ARC 68—69 Arc length 104 arc, analytic 226 arc, differentiable 69 arc, opposite 69 Arc, rectifiable 104—105 arc, regular 69 Arc, simple 69 Argument 13 46 Argument principle 151—153 Artin, E. viii 144 Arzela — Ascoli theorem 214 Associative law 4 Asymptotic development 203 Automorphic function 270 Axis, imaginary 12 Axis, real 12 Barrier 242 Basis 258 bernoulli 203 bessel 304 Binomial equation 15—16 Bolzano — Weierstrass theorem 63 Borel 60 Boundary 53 Bounded 56 Bounded variation 105 Branch 277 Branch point 98 287—291 Calculus of residues 147—160 Canonical basis 260 Canonical mapping 243—253 Canonical product 192—196 Canonical region 243 Cantor, G. 64 214 Caratheodory, C. 235 Cauchy estimate 122 Cauchy inequality 10 Cauchy integral formula 118—120 Cauchy integral theorem 109—114 137—147 Cauchy principal value 157 Cauchy sequence 34 Cauchy — Riemann equations 25—26 Cauchy, A. 25 Chain 137—138 Change of parameter 68 Circle of convergence 39 Closed curve 69 Closed, definition 52 Closure 53 Commutative law 4 Compact 59—64 Complement 50 Complex function 21—48 Complex integration 101—172 Component 57 Conformal equivalence 243 Conformal mapping 13—76 221—253 Congruence subgroup 270 Conjugate differential 162 Conjugate harmonic function 25 Conjugate number 6—8 Connected sets 54—59 Connectivity 144—147 Continuation along arc 278—281 Continuation, analytic 275—280 Continuation, analytic, direct 279 Continuous function 64—67 Continuous function, uniformly 66 contour 109 Contraction 35 Convergence, absolute 36 Convergence, circle of 39 Convergence, uniform 37 Convergent sequence 34 Cross ratio 78—80 Curve 68 Curve, Jordan 69 Curve, level 89 Curve, point 69 Curve, unit 284 CYCLE 138 De Moivre 15 Definite integral 101 Deformation 281 Dense 58 Derivative 23 24 Differentiable arc 69 Differential equation 267—269 299—312 Dirichlet's problem 240—243 Discrete 59 257 Discriminant 292 Distributive law 4 Divergent sequence 34 Doubly periodic function 257 Element 50 ellipse 95 Elliptic function 232 Elliptic integral 231 Elliptic modular function 270 Elliptic, definition 86 Empty set 53 Entire function 192 205—210 Equicontinuous 210—211 Essential singularity 129 Euler, L. 44 197 Exact differential 107 Exponential function 43—46 Exterior 53 Fibonacci numbers 182 Field 4 Fixed point 86 Fourier development 256 Fraction, partial 31 185—189 Fresnel integral 205 Function element 275 Function, algebraic 291—297 Function, analytic 24—28 69—76 Function, analytic, complete 276 Function, analytic, global 275 Function, complex 21—48 Function, conjugate harmonic 25—26 Function, continuous 23 64—67 Function, entire 192 205—210 Function, exponential 43—46 Function, Gamma 196—205 Function, Green's 243 249—251 Function, harmonic 25 160—172 233—243 Function, hypergeometric 308 Function, integral 192 Function, inverse 65 Function, regular 127 Function, single-valued 22 Functional relation 277 Functional, definition 167 Functions, subharmonic 237—240 Functions, trigonometric 43—46 Fundamental group 284 Fundamental region 98—99 274 Fundamental sequence 34 Fundamental theorem of algebra 28 122 Gamma function 196—205 Geometric series 38 Germ 277 Global analytic function 275 Goursat, E. 11 Greatest lower bound (g.l.b.) 55 Green's function 243 249—251 Hadamard formula 39 Hadamard, J. 206—210 Harmonic function 25 160—172 233—243 Harmonic measure 244—249 Harnack's principle 235—237 Heine — Borel 60 Holomorphic 21 24 Homeomorphism 65 Homologous, definition 144 Homology basis 146 Homomorphism 46 Homothetic, definition 77 Homotopic 281—287 Hurwitz, A. 176 217 Hyperbola 90 95 Hyperbolic, definition 86 Hypergeometric differential equation 305—309 Hypergeometric function 308 Identity, Lagrange's 9 Image 64 73 Imaginary axis 12 Imaginary part 1 INDEX 114—118 Indicial equation 303 Indirectly conformal 75 inf 55 Infinite product 189—192 infinity 18 Integral domain 4 Integral function 192 Integral, complex 101—104 Integral, definite 101 Integration 101—172 Interior 53 Intersection 50 interval 55 Into, definition 64 Inverse function 65 Inverse image 65 inversion 77 Involutory transformation 7 Isolated point 53 Isolated singularity 124 Isomorphism 5 Jacobian 25 75 Jensen's formula 205—206 Jordan arc 69 Jordan curve 69 Jordan curve theorem 118 Kernel 46 Koebe, P. 222 Lacunary value 297 Lagrange's identity 9 Laplace equation 25 160 Laurent series 182—184 Least upper bound (l.u.b.) 55 Legendre polynomial 182 Legendre relation 266 Length 104 Level curve 89 Limes inferior 34 Limes superior 34 LIMIT 22—24 Limit point 62 Lindelof, E. viii 97 199 Line integral 101—109 Linear differential equation 299—312 Linear group 76—78 Linear transformation 76—89 Liouville's theorem 122 Local mapping 130—133 Local solution 299 Locally bounded 216 Locally exact 144 Logarithm 46—48 Lucas theorem 29 Majorant 37 Mapping theorem, Riemann's 221—227 Mapping, conformal 68—76 227—233 Mapping, continous 64—67 Mapping, local 130—133 Mapping, slit 251—253 Mapping, topological 65 Maximum 56 Maximum principle 133—137 164 Mean-value property 163—165 234—235 Measure, harmonic 244—249 Meromorphic, definition 128 Minimum 56 Minorant 37 Mittag-Leffler, G. 185 Modular function 269—270 Modular group 259 Module 146 257—258 Modulus 7 Monodromy theorem 285—287 Morera's theorem 122 Multiply connected regions 144—147 Neighborhood 52 Noneuclidean distance 137 Noneuclidean length 137 Normal derivative 162 Normal family 210—219 One to one 65 Onto, definition 65 open 52 Order of branch point 98 Order of entire function 207 Order of pole 30 127 Order of rational function 31 Order of zero 29 127 Order relation 5 Order, algebraic 128 Ordinary point 300 Orientation 83 Osgood, W.F. 222 parabola 90 Parabolic, definition 86 PARAMETER 68 Parameter, change of 68 Parameter, linear 68 Partial fraction 31 185—189 Period 45—46 255 Perron, O. 240 Picard theorem 297—298 piecewise 69 Plane, complex 12 Plane, extended 18 Point curve 69 Point, accumulation 53 Point, branch 98 287—291 Point, fixed 86 Point, isolated 53 Point, limit 62
Реклама
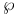-function 
|
|
О проекте